Развитие технологических университетов с многоуровневым и многопрофильным образованием должно обеспечить фундаментальность и глубину современного высшего образования, создать у студента мыслительный аппарат, который позволит идти в ногу с техническим прогрессом, сформировать у него умение определять существующие профессиональные проблемы и находить оптимальные пути их решения. Все эти задачи, поставленные перед высшим образованием, требуют пересмотра его наполнения, усиления профессиональной ориентации и, как следствие, требуют изменения содержания высшего математического образования и методики преподавания. При этом эффективность и качество обучения математике должны определяться уровнем математического развития студентов, степенью их подготовки к самостоятельному овладению знаниями.
Современное общество требует от выпускников высших учебных заведений владения знаниями и умениями, позволяющими им не только решать текущие задачи и проблемы, но и развиваться вместе с техническим прогрессом. Другими словами, выпускник вуза должен обладать набором определенных профессиональных компетенций, и профессиональная компетентность рассматривается как один из основных показателей уровня подготовки современного специалиста. Развитие общества влечет за собой постоянное изменение требований к необходимым компетенциям специалиста. Актуальность вопроса формирования профессиональных компетенций очевидна. Его решение – объемная задача, требующая разработки соответствующей системы профессионального образования и, в частности, математического образования как базовой составляющей многих современных компетенций и ее практического применения [1].
Цель исследования - раскрыть проблемы формирования математических и профессиональных компетенций при изучении математики и предложить пути их реализации.
Материал и методы исследования
Направление 18.03.01 «Химическая технология» – одно из основных в Казанском национальном исследовательском технологическом университете (КНИТУ (КХТИ)). При изучении дисциплины «Математика» государственным стандартом для данного направления предусмотрено формирование профессиональных компетенций в виде готовности применять аналитические и численные методы решения поставленных задач, а приоритетной задачей подготовки кадров для химической промышленности является задача формирования профессиональной компетентности специалиста, бакалавра, магистра.
В работе [2] решение данного вопроса видится в использовании практической ориентированности процесса обучения. В работе [3] формирование компетентности специалистов, состоящее в единстве как знаний и умений, так и личностных качеств, предлагается для выполнения различных видов профессиональной и социальной деятельности. Эта задача остается актуальной ввиду необходимости разработки и применения соответствующей системы профессионального образования, в частности математического образования [4].
Перед преподавателем встает непростая задача создания педагогических условий при формировании необходимых математических и профессиональных компетенций. Требуется сохранить целостность, глубину и системность в понимании методов и приемов математики при сокращении объема часов, выделенных на изучение предмета.
До 2016 г. общая трудоемкость дисциплины «Математика» для направления «Химическая технология» составляла 16 зачетных единиц, или 576 часов, распределенных на 3 семестра. С 2017 г. количество часов уменьшилось до 540 часов, т.е. 15 зачетных единиц. Изменения, связанные с уменьшением часов, данных на изучение предмета «Математика» («Высшая математика»), произошли и для бакалавров и специалистов различных технологических специальностей, таких как 29.03.04, 29.03.01, 18.05.01, 21.05.04.
Казалось бы, уменьшение несущественно – 36 часов. Но это изменение связано прежде всего с уменьшением объема аудиторной работы со студентами, когда преподаватель может помочь сориентироваться в большом многообразии существующих математических методов и моделей, поделиться своим опытом решения профессионально значимых вопросов и задач. Перед преподавателем встает вопрос: чем жертвовать в создавшихся условиях, учитывая постоянно растущий объем необходимых знаний и умений и недостаточно высокую школьную подготовку студентов-химиков по математике? Как в подобной ситуации «приблизить» студентов к их будущей профессиональной деятельности? Очевидно, что задача формирования профессиональной компетентности будущего специалиста требует высокой профессиональной компетентности прежде всего самого преподавателя. Преподаватель высшей школы должен не только давать знания по своему предмету, но и раскрывать их связи с будущей профессиональной деятельностью, уметь видеть перспективные математические методы и модели для постоянно развивающегося общества. Все эти задачи требуют расширения математического и научного кругозора самих преподавателей.
Большую пользу в решение задачи формирования профессиональных компетенций студентов вносит совместная работа преподавателей математики и преподавателей профессионального цикла. Их сотрудничество способствует постоянному обновлению практического содержания курса как математики, так и курсов профессионального цикла.
Успешное внедрение компетентностного подхода при изучении математики невозможно без создания определенной методической базы, включающей в себя, кроме теоретического курса предмета, еще и прикладные и профессионально ориентированные задачи разного уровня по направлениям обучения, математические модели этих задач и методы их решения, методы интерпретации полученных результатов.
Совершенно очевидно, что для достижения достойных результатов в той или иной деятельности необходима серьезная мотивация. Как быть в нашем случае? Если дисциплина «Математика» изучается на младших курсах: бакалавры – 1–3-й семестр, для специалистов добавлен еще 4-й семестр, то предметы по специальности – на старших. В результате студенты не видят связи между математикой и своей будущей специальностью, у них не возникает соответствующей потребности к изучению предмета. А ведь именно потребность и формирует мотивацию, способствуя более осмысленному изучению той или иной темы, соответственно развивая математические способности. Следовательно, преподаватель должен преподнести изучаемый материал таким образом, чтобы студенты
почувствовали его значимость, проявили интерес. Один из подобных методов управления познавательной деятельностью студентов – включение междисциплинарных и профессионально ориентированных задач [5]. Для усиления мотивации студентов при изучении математики, для развития их математических способностей профессионально ориентированные задачи, на наш взгляд, должны удовлетворять следующим условиям:
– задача должна описывать проблему будущей профессиональной деятельности студентов данного направления;
– свойства изучаемого объекта исследуются с использованием математического аппарата;
– решение рассматриваемой задачи должно помочь студентам в овладении математическими знаниями и умениями. Кроме того, формулировка задачи должна быть лаконичной, методы решения – просты и понятны, вычисления – нетрудоемки по времени. В противном случае теряется вся суть использования математических методов при решении прикладной задачи.
Приведем примеры иллюстрации подобного подхода.
При изучении раздела «Линейная и векторная алгебра» (в частности, рассматривая линейную зависимость и независимость векторов) полезно предложить для решения следующую задачу [6].
Описание проблемы
Процесс получения СО2 при взаимодействии водяного пара с углем можно описать следующими четырьмя реакциями:
Н2О + С = СО + Н2
Н2О + СО = Н2 + СО2
2СО = CО2 + С
2Н2О + С = 2Н2 + СО2
Среди данных уравнений могут присутствовать такие, которые относятся к комбинации двух или более реакций данной системы (линейно зависимые реакции). Они не несут дополнительной информации о реакционной системе, и их можно удалить, понизив таким способом размерность полученной системы уравнений и упростив решение задачи.
Требуется: 1) определить число линейно независимых реакций; 2) определить линейно зависимые реакции данной системы; 3) показать линейную независимость соответствующих реакций.
При решении задач кинетики множество уравнений химических реакций рассматриваются как линейное пространство, и для отыскания линейно независимых реакций удобно воспользоваться математическим аппаратом линейной и векторной алгебры, изучаемым в первом семестре курса высшей математики [7].
Решение задачи 1).
Применяемый математический аппарат: свойство матриц, действия над матрицами.
Введем обозначения A1 = Н2O, А2 = С, А3 =СО, А4 = Н2, А5 = СО2 , запишем реакции в виде системы однородных алгебраических уравнений:
–A1 – A2 + A3 +А4 = 0
– А1 – А3+А4+А5 = 0
А2 – 2А3 + А5 = 0
- 2А 1 – А2 +2А4+А5 = 0
Векторами уравнений рассматриваемых реакций будут: 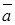 1={–1, –1, 1, 1, 0};
1={–1, –1, 1, 1, 0}; 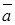 2={–1, 0, –1, 1, 1};
2={–1, 0, –1, 1, 1}; 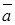 3 ={0, 1, –2, 0, 1};
3 ={0, 1, –2, 0, 1}; 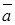 4={–2, –1, 0, 2, 1}.
4={–2, –1, 0, 2, 1}.
Число независимых реакций данной системы равно рангу матрицы, составленной из стехиометрических коэффициентов.
Имеем:
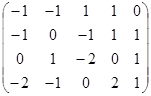 ~
~ 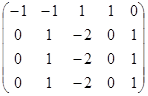 ~
~ 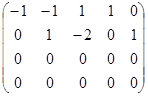 .
.
Ранг преобразованной матрицы равен 2 (первую строку, умноженную на (–1), прибавили ко второй; умноженную на (–2) прибавили к четвертой).
Вывод. Данная система имеет две линейно независимые реакции.
Решение задачи 2).
Применяемый математический аппарат: методы решения систем линейных алгебраических уравнений. Векторы 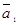 ,
, 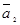 ,
, 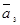 ,
, 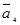 линейно независимы, если существуют числа
линейно независимы, если существуют числа 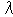 i (i=
i (i=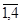 ), такие, что равенство
), такие, что равенство 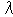 1
1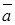 1+
1+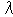 2
2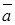 2+
2+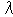 3
3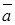 3+
3+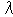 4
4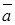 4 = 0 выполняется лишь при условии, что все
4 = 0 выполняется лишь при условии, что все 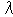 i (i=
i (i=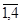 ) равны нулю. Методом подбора легко найти отличные от нуля
) равны нулю. Методом подбора легко найти отличные от нуля 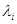 , например при
, например при  координаты вектора получаются равными нулю:
координаты вектора получаются равными нулю:
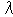 1
1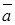 1 +
1 + 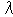 2
2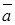 2 +
2 + 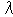 3
3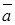 3 +
3 + 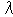 4
4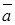 4 = – 3 – 1 + 4; 3 – 1 – 2; 3 + 1– 4; 1 + 1– 2}. Система из четырех реакций линейно зависима.
4 = – 3 – 1 + 4; 3 – 1 – 2; 3 + 1– 4; 1 + 1– 2}. Система из четырех реакций линейно зависима.
Исключим из системы реакций четвертую, оставшиеся три тоже линейно зависимы, так как при наборе 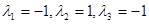 линейная комбинация
линейная комбинация 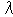 1
1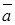 1+
1+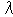 2
2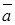 2+
2+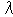 3
3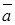 3= 0.
3= 0.
Наконец, исключив из системы третью реакцию и проверив на линейную независимость оставшиеся, получим, что они линейно независимы, так как координаты вектора 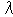 1
1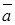 1+
1+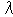 2
2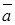 2 равны нулю тогда и только тогда, когда
2 равны нулю тогда и только тогда, когда 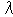 1 =
1 =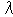 2 = 0 .
2 = 0 .
Вывод. Таким образом, из рассматриваемых четырех реакций третья и четвертая, являясь линейной комбинацией первой и второй реакций, являются линейно зависимыми: вычитая из второй реакции первую, получаем:
Н2О + С = СО + Н2
– Н2О + СО = Н2 + СО2
------------------------------------
2СО = CО2 + С (третья реакция).
Складывая первую и вторую реакции, имеем четвертую:
Н2О + С = СО + Н2
+ Н2О + СО = Н2 + СО2
---------------------------------
2Н2О + С = 2Н2 + СО2
Следовательно, из системы уравнений можно удалить третью и четвертую реакцию, в результате чего получим следующую систему:
Н2О + С = СО + Н2
Н2О + СО = Н2 + СО2
Решение задачи 3).
Применяемый математический аппарат: вычисление определителей; вычисление скалярного произведения векторов. Линейную независимость первой и второй реакций системы покажем, используя определитель Грама, составленный из скалярных произведений векторов 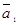 и
и 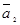 : векторы
: векторы 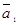 и
и 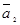 линейно независимы в том и только в том случае, если определитель Грама отличен от нуля. Вычислим скалярные произведения:
линейно независимы в том и только в том случае, если определитель Грама отличен от нуля. Вычислим скалярные произведения: 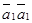 = 1 + 1 + 1 + 1 = 4,
= 1 + 1 + 1 + 1 = 4, 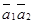 = 1 + 0 – 1 + 1 + 0 =1,
= 1 + 0 – 1 + 1 + 0 =1,  = 1 + 0 + 1 + 1 + 1 = 4. Тогда
= 1 + 0 + 1 + 1 + 1 = 4. Тогда
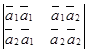 =
= 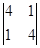 = 15.
= 15.
Вывод. Определитель Грама отличен от нуля, первая и вторая реакции исходной системы линейно независимы.
По аналогии с предыдущими исследованиями легко показать, что исходная система четырех реакций линейно зависима. Составим определитель Грама из скалярных произведений 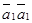 ,
, 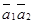 ,
, 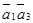 ,
, 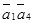 ,
,  ,
, 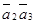 ,
, 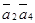 ,
, 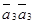 ,
, 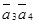 ,
,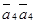 .
.
В этом случае имеем:
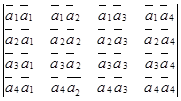 =
= 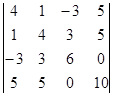 = 0.
= 0.
Результаты исследования
Включение подобных задач в стандартный курс высшей математики показывает практическую значимость математических методов и моделей, повышает мотивацию студентов к изучению высшей математики.
Заключение
Преподавателями кафедры высшей математики КНИТУ была сформирована и апробирована база профессионально ориентированных задач, созданная для направлений 29.03.04, 29.03.01, 18.05.01, 21.05.04 при обучении студентов. В образовательном процессе использовались методы проблемного обучения с применением эвристического и исследовательского подхода в формировании знаний и умений. Диагностика уровня cформированности деятельностной профессиональной компоненты проводилась с помощью тестов различного уровня сложности, содержащих комбинированные компетентностно ориентированные задания. Использование профессионально значимых задач при проведении аудиторных занятий, а также при составлении индивидуальных расчетных домашних заданий привело к усилению заинтересованности у студентов к изучению математики, овладению математическими методами и моделями, увеличению активности и творчества, их личностному росту. Применение систем междисциплинарных задач обеспечивает мотивацию обучения студентов, позволяет готовить специалистов, умеющих мыслить и действовать категориями, необходимыми для решения современных инженерных задач.



