Реализация компетентностного подхода, взаимосвязь академических знаний и практических умений являются обязательными условиями повышения качества подготовки будущих педагогов. Современные технологии обучения осуществляют связь теоретической подготовки бакалавров педагогического вуза с их будущей профессиональной деятельностью, особенно выделяются технологии проектного обучения [1].
В работе [2] отмечена необходимость перехода от информативных форм обучения к активным. Однако главными задачами обучения студентов математических специальностей по-прежнему остаются приобретение классических знаний, формирование математического мышления и подготовка к научной деятельности. Метод проектирования объединяет новые подходы и традиционное обучение.
Организация проектной деятельности бакалавров обусловлена модернизацией системы высшего образования на основе системно-деятельностного и компетентностного подходов [3, 4]. Довольно подробно проработана теория технологии проектного обучения для начального и общего образования, накоплен практический опыт ее использования в учебном процессе и внеурочной деятельности. В то же время для системы высшего образования теоретических и практических разработок использования проектной деятельности еще недостаточно [5].
Внедрение в работу образовательных учреждений ФГОС ВО 3++ требует от вузов совершенствования учебно-методических материалов, организации учебного процесса и повышения профессионального уровня профессорско-преподавательского состава.
Материалы и методы исследования
В формирование профессиональных компетенций будущих учителей математики основной вклад вносит изучение профильных математических дисциплин. Наиболее оптимальной для формирования профессиональной компетенции является технология учебных проектов междисциплинарной тематики. Выполнение таких проектов способствует росту доли самостоятельной работы студентов, их активному участию в образовательном процессе.
Для направления подготовки Педагогическое образование в ЮУрГГПУ большинство учебных планов имеют двойную профильную направленность. Так, на физико-математическом факультете ведется обучение по таким профилям, как: Математика. Информатика, Физика. Математика.
Руководство учебно-исследовательской деятельностью школьников является профессиональной компетенцией учителя математики, и процесс ее формирования зависит от глубины знания и понимания основ современной математики и ее приложений. Освоение ключевых понятий алгебры, математического анализа, геометрии позволяет реализовать проекты в области математики, физики, информатики: построение таблиц характеров [6], описание групповых колец и поиск их обратимых элементов [7], прикладное программирование, дифференциальные уравнения, волноводы сложной структуры. Изучение методики обучения и воспитания на третьем и четвертом курсах создает основу для реализации методических проектов в рамках изучения школьных предметов «Математика», «Информатика», «Физика», а также позволяет апробировать результаты исследований в ходе педагогических практик. Такие проекты могут быть реализованы в групповой или индивидуальной формах при написании курсового проекта на третьем или четвертом курсе.
Результаты исследования и их обсуждение
Анализ научной и методической литературы, а также опыт реализации учебных проектов при предметной подготовке будущих учителей математики позволяют нам заключить, что эффективная организация процесса обучения, нацеленного на формирование профессиональных компетенций средствами проектной деятельности [8, 9], должна включать следующие этапы: информационно-поисковый, этап реализации, этап рефлексии.
«Сдвоенный бакалавриат» направления подготовки Педагогическое образование направленности Математика. Информатика позволяет сформулировать темы междисциплинарных проектов, связанных с выполнением сложных алгебраических вычислений посредством GAP (Groups, Algorithms and Programming), которая является системой компьютерной алгебры, задуманной как инструмент вычислительной теории групп и впоследствии распространившейся на смежные разделы алгебры. GAP является свободно распространяемой, открытой и расширяемой системой. Система поставляется вместе с исходными текстами, которые написаны на двух языках: ядро системы написано на Си, а библиотека функций – на специальном языке, также называемом GAP, который по синтаксису напоминает Pascal, однако является объектно-ориентированным языком. Существует возможность записи результатов вычислений и выполняемых команд в текстовые файлы.
В работе [10] в теореме 3 получена формула для вычисления ранга группы центральных единиц целочисленных групповых колец метациклических групп Фробениуса с ядром порядка m и дополнением порядка n. Следствия 1–3 [10] подробно рассматривают случай с простым m и рангом, равным 0 и 1, вопрос о выявлении случаев с рангом 2, 3 и далее требует все более объемных вычислений и временных затрат.
Задача1: Вычислить значения рангов по формуле для простого m, не превосходящего 1000.
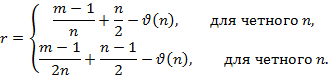
Здесь 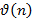 – число всех натуральных делителей числа
– число всех натуральных делителей числа 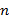 .
.
Для решения поставленной задачи на информационно-поисковом этапе потребовалось изучение теоретического материала алгебры и теории чисел, в частности рассмотрены понятия: «метациклическая группа», «группа Фробениуса», «групповое кольцо», «обратимый элемент», «центральный элемент», «функции числа всех натуральных делителей», «простые числа», «четные и нечетные числа». Отметим, что большинство этих понятий не входит в курс алгебры, является материалом для самостоятельного изучения.
Также было необходимо освоение программирования в системе GAP4. Работа в этой системе требует значительной аккуратности, так как отсутствует возможность копирования блока команд, для внесения изменений необходимо повторить всю последовательность команд.
Для решения задачи команда студентов разделилась на мини-группы: одни составляли алгоритм решения задачи, другие реализовали его в программной оболочке, третьи проверяли полученные результаты, четвертые оформляли текстовый документ и презентацию для доклада о результатах проекта. В системе компьютерной алгебры GAP4 упорядоченный список «Primes» содержит 168 простых чисел, не превосходящих 1000. Решение задачи было организовано двумя вложенными циклами, счетчик которых принимал значения предварительно заданных множеств, условный оператор позволял вычислять ранг в зависимости от четности числа n. Кроме того, для некоторых значений m требовалось выполнить вычисления по формуле вручную для верификации алгоритма. Результат, записанный программой в текстовый файл, неудобен для дальнейшего анализа и выявления закономерностей, он был переработан в таблицу. Приведем ее фрагмент для простых m, не превосходящих 20, в таблице.
Значения рангов для простых m, не превосходящих 20
|
m |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
||||||||||||||||
|
n |
2 |
2 |
4 |
2 |
3 |
6 |
2 |
5 |
10 |
2 |
3 |
4 |
6 |
12 |
2 |
4 |
8 |
16 |
2 |
3 |
6 |
9 |
18 |
|
r |
0 |
1 |
0 |
2 |
0 |
0 |
4 |
1 |
2 |
5 |
1 |
2 |
1 |
1 |
7 |
3 |
2 |
4 |
8 |
2 |
2 |
2 |
4 |
На этапе рефлексии организован круглый стол, где каждый участник проекта дал оценку деятельности остальных, высказал пожелания по организации учебных проектов и выделил основные трудности, возникающие при их реализации.
В рамках реализации «сдвоенного бакалавриата» направления подготовки Педагогическое образование направленности Физика. Математика была сформулирована задача по решению волнового уравнения для студентов 3–4-го курсов. Для решения поставленной задачи на информационно-поисковом этапе потребовалось изучение теоретического материала математического анализа – таких разделов, как «Дифференциальные уравнения» и «Уравнения в частных производных», а также материала курса «Общая и экспериментальная физика (оптика)»: волновые уравнения, волноводы, распределение показателя преломления. Для решения поставленной задачи потребовалось углубленное самостоятельное изучение этих понятий – как с точки зрения разделов математического анализа, так и с точки зрения разделов оптики.
Задача 2. [11] Получить решение волнового уравнения для распределения E(y) светового поля для каждого слоя волноводной структуры, представленной на рисунке:
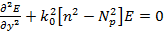 ,
,
где 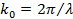 ,
, 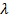 – длина волны излучения;
– длина волны излучения; 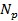 – эффективный показатель преломления волноводной моды с номером p.
– эффективный показатель преломления волноводной моды с номером p.
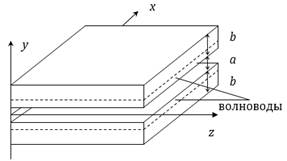
Сложная волноводная структура
Распределение показателя преломления n(y) волны в рассматриваемой структуре задается следующей ступенчатой функцией [12]:

где 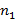 и
и 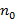 – показатели преломления излучения в воздушной среде и в пластинах из нелинейного материала соответственно. Для структуры на основе воздушной среды
– показатели преломления излучения в воздушной среде и в пластинах из нелинейного материала соответственно. Для структуры на основе воздушной среды 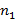 =1;
=1; 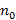 – показатель преломления структуры.
– показатель преломления структуры.
Решения уравнения для каждого из слоев с учетом условия конечности представим в виде
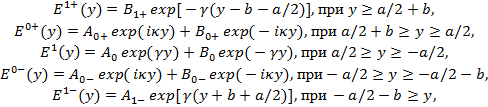
где постоянная затухания поля вне пластин и поперечная постоянная распространения в волноводном слое определяются выражениями: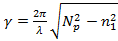 ,
, 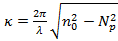 .
.
Полученные результаты были представлены на студенческой конференции и рекомендованы к публикации. На этапе рефлексии участники заполнили разработанные опросники, позволяющие получить оценку проектных умений, а также определить достаточность уровня предметной подготовки студентов для решения научно-исследовательских задач.
Учитывая педагогическое направление подготовки, будущим выпускникам важно научиться применять знания профильных математических дисциплин в профессиональной деятельности учителя. В одном из методических учебных проектов поставлена задача подобрать комплекс упражнений и задач, помогающих в преодолении трудностей, возникающих у школьников в процессе изучения темы «График функции». Особенно ценным стал факт запроса такого комплекса от образовательной организации, в которой студенты проходили педагогическую практику.
На информационно-поисковом этапе группа студентов определяла место темы «График функции» в школьном курсе математики на основе учебно-методических комплексов по математике для 5–11-х классов следующих авторов: А. Г. Мерзляка, Г. В. Дорофеева, Г. К. Муравина, С. М. Никольского. В ходе изучения результатов ЕГЭ и ОГЭ, а также педагогической практики и беседы с учителями образовательных организаций был собран материал, позволяющий определить основные трудности, с которыми сталкиваются обучающиеся общеобразовательной школы при изучении темы «График функции».
Далее на этапе реализации студенты выделили навыки, которые необходимо сформировать для успешного освоения темы, и подобрали упражнения, направленные на формирование конкретного навыка:
1) навык определения по графику абсциссы точки по заданной ординате или ординаты точки по заданной абсциссе;
2) навык определения зависимых и независимых величин;
3) связь между формулой, задающей зависимость, таблицей ее значений и графиком, ее иллюстрирующим;
4) умение «считывать» по графику функции ее свойства: область определения и область значений, наибольшее и наименьшее значения функции на промежутке, четность и нечетность функции;
5) навык построения графика функции с помощью элементарных преобразований на основе графиков элементарных функций;
6) навык графического решения систем уравнений и неравенств с двумя переменными;
7) использование производной для исследования свойств функции и построения эскиза ее графика.
Составленный комплекс упражнений был апробирован в ходе педагогической практики и показал эффективность в формировании перечисленных навыков. Результаты проекта стали основой для квалификационной работы.
На этапе рефлексии организован круглый стол с участием представителей образовательной организации, где каждый участник проекта дал оценку деятельности остальных, высказал пожелания по организации учебных проектов и выделил основные трудности, возникающие при их реализации.
Выводы
Описанные учебные проекты, реализованные при обучении профильным математическим дисциплинам бакалавров физико-математического факультета по направлению подготовки Педагогическое образование с направленностью Математика, Информатика и Физика. Математика показали, как взаимосвязаны академические знания и практические умения, теоретическая подготовка в рамках отдельных профильных дисциплин и научно-исследовательская и проектная деятельность бакалавров.
Анализ результатов и этап рефлексии позволили скорректировать и разнообразить тематику предлагаемых студентам учебных проектов, выявили необходимость регулярного контроля деятельности участников проекта со стороны руководителей, а также поиска новых форм организации растущего объема самостоятельной работы студентов и пересмотра структуры и содержания профильных дисциплин, актуализации их практической составляющей.
Работа выполнена при финансовой поддержке ФГБОУ ВО «Шадринский государственный педагогический университет» по договору о выполнении НИР № 16-382 от 28.05.2019.



