Перед выпускниками высших учебных заведений ставится большая задача: быть самостоятельными, конкурентоспособными, компетентными в своей профессиональной деятельности. Главная задача образования в высшей школе - это подготовка профессиональных кадров. Одним из подходов для достижения этой задачи в системе высшего образования является компетентностный подход. Компетентностный подход предполагает подготовку специалиста, демонстрирующего высокую эффективность работы, быструю адаптацию к меняющимся жизненным условиям [1].
В современном образовательном процессе постоянно меняются, усовершенствуются новые педагогические технологии. И, как считают Грибкова Ю.В., Кашинцева О.А., Сарычева И.А., усиливается прикладная и практическая составляющая в обучении будущих специалистов [2]. Одним из таких педагогических технологий в организации образовательной деятельности студентов является метод проектов. В педагогической литературе данное понятие встречается во многих работах педагогов-ученых ХХ века (А.Н. Алексеев, В.А. Сластенин, И.Ф. Исаев, А.И. Мищенко, Е.Н. Шиянов). Так, В.А. Сластенин, И.Ф. Исаев, Е.Н. Шиянов определяют педагогический проект как содержательное, организационно-методическое, материально-техническое и социально-психологическое оформление замысла реализации целостного решения педагогической задачи, осуществляемой на эмпирическо-интуитивном, опытно-логическом и научном уровне.
Н.О. Яковлева рассматривает педагогическое проектирование как целенаправленную деятельность по созданию проекта в виде инновационной модели образовательно-воспитательной системы, ориентированной на массовое использование.
Мы согласны с мнениями Грибковой Ю.В., Кашинцевой О.А., Сарычевой И.А. о том, что метод проектов является одним из путей демонстрации студентам места математики и ее методов в современной науке и практической деятельности, применения математических знаний в предстоящей профессиональной деятельности [2].
В своей работе С.Г. Щербакова определяет, что метод проектов - это набор техник и приемов, позволяющих создавать образовательные ситуации, в которых учащийся ставит и решает собственные проблемы [3]. Сущность метода проектов, методика осуществления проектной деятельности отражены во многих работах педагогов-ученых [1; 3; 4].
Метод проектов дает возможность организовать учебную деятельность, соблюдая разумный баланс между теорией и практикой, развивает интеллектуальное и нравственное развитие студентов, помогает сплотиться и работать в команде, повышает ответственность за совместную работу [3]. В литературе выделяют три основных вида проектной деятельности: творческая, исследовательская, нормативная.
Целью нашего исследования является:
- ознакомить студентов с одним из методов современной технологии – методом проектов;
- показывать применение математических знаний в профессиональной деятельности;
- развивать познавательную самостоятельность студентов; способствовать умению анализировать, обобщать, добиваться поставленной цели.
Материал и методы исследования: теоретико-поисковый метод, сопоставление и обобщение практического опыта, беседа, наблюдение. Внедрение проектной деятельности в процессе обучения математике мы осуществляли среди студентов первого курса факультета ветеринарной медицины ФГБОУ ВО «Якутская государственная сельскохозяйственная академия». При изучении каждого раздела дисциплины «Математика и математические методы в биологических процессах» мы вводили элементы проектной деятельности, решали профессионально ориентированные задачи.
В качестве примера приведем внедрение элементов метода проектов при изучении темы «Применение дифференциальных уравнений в естествознании». При изучении данного материала мы не только предоставляли теоретические основы дифференциальных уравнений, но и рассматривали основные математические модели биологических процессов, в которых применяются дифференциальные уравнения. Проектная деятельность студентов состояла из трех этапов:
- подготовительный этап (поисковый): сбор и изучение информации; анализ имеющейся информации по проекту; определение и анализ проблемы проекта; моделирование заданной ситуации);
- основной этап (аналитический): постановка цели и задачи проекта, определение способов и методов проведения проектной деятельности; составление плана реализации проекта; выполнение проектной деятельности по плану;
- заключительный этап (презентационный): предварительная оценка проекта; планирование и составление презентационного материала; презентация проекта, анализ результатов выполнения работы [5-7].
Для формирования общекультурных и общепрофессиональных компетенций у будущих студентов-аграриев, обучающихся по направлению 06.03.01 «Биология» (направленность «Охотоведение»), при изучении данной темы мы ставили перед собой следующие цели:
- учебные цели: научить студентов составлять математические модели процессов с использованием дифференциальных уравнений; научить решать задачи профессионального характера с использованием дифференциальных уравнений, показать значимость применения дифференциальных уравнений при изучении биологических процессов;
- развивающие цели: усилить мотивацию к изучению дисциплины; формировать и развивать профессиональные навыки обучающихся, навыки владения современными техническими средствами и технологиями;
- воспитательные цели: воспитать культуру общения, повысить грамотность устной речи у студентов.
На подготовительном этапе изучения раздела «Дифференциальные уравнения» студенты изучали теоретическую часть раздела и распределялись в группы по 4-6 человек для совместного изучения выбранной темы. Перечислим проектные темы, предложенные студентам для самостоятельного изучения: количество населения на определенную дату; истощение ресурсов; дифференциальная модель популяции животного мира; модели динамики популяций; простая модель «хищник-жертва» (модель Лотки-Вольтерры); модель роста фитопланктона; одномерная модель распространения загрязняющих веществ; динамические модели в биологии и экологии; современная классификация моделей биологических процессов (регрессионные, имитационные, качественные модели); управление биологическими процессами в биотехнологии и сельском хозяйстве. Каждая группа выбирала интересующую тему. В течение 1-2 недель студенты работали над своим проектным заданием. Через определенное время студенты на практическом занятии защищали проектные работы в виде презентаций.
Этапы реализации проекта «Применение дифференциальных уравнений в естествознании» студентами:
1. Постановка проблемы. Какие биологические процессы описываются с помощью дифференциальных уравнений.
2. Постановка цели проекта. Цель проекта – метод решения практико-ориентированной задачи.
3. Планирование работы над проектом. Планируются основные этапы, сроки выполнения, распределяются обязанности.
Представим сценарий итогового практического занятия, где каждая группа выступала со своими выполненными проектными работами:
1. Подготовительный этап. Преподаватель сообщает цели, задачи занятия.
2. Мотивационный этап. Преподаватель повторяет, с использованием мультимедиапрезентации, такие понятия, как математическое моделирование, биологические процессы, роль математического аппарата при решении задач биологии, экологии, математическая модель, дифференциальное уравнение, а также описание биологических процессов с использованием дифференциальных уравнений. Под руководством преподавателя студенты начинают заполнять таблицу наиболее важными сведениями из выступлений своих однокурсников (табл. 1) [8].
3. Ознакомление с новым материалом. После выступления каждого докладчика (из каждой группы выступает один человек) все студенты обсуждали доклад своего однокурсника. Преподаватель особое внимание уделял методам и способам решения дифференциальных уравнений, а также отмечал то, что различные по своей природе процессы описываются похожими дифференциальными уравнениями, что говорит об универсальности математического описания объектов реального мира.
Таблица 1
Различные процессы, описываемые с помощью дифференциальных уравнений первого порядка (по Масыгиной И.А.)
|
Задача |
Дифференциальное уравнение |
Общее и частное решения |
|
Распределение температуры внутри ограждающей поверхности |
х - расстояние до наружной стены; t - температура на расстоянии х; k - коэффициент теплопроводности. |
Общее решение:
частное решение: за сутки 1 м2 кирпичной стены при температуре воздуха 0 °С отдаёт наружу 320 Ккал. |
|
Нагрев тел |
Q - количество теплоты, необходимое для нагрева; t - температура. |
Общее решение:
частное решение: для нагрева 1 кг железа от 20 до 21 °С необходимо 0,11 Ккал. |
|
Охлаждение тел |
Т - температура хлеба; t - температура окружающей среды; k - коэффициент теплопроводности;
|
Общее решение:
частное решение: при температуре воздуха 25 °С температура хлеба понизится от 100 до 30 °С за 71 минуту. |
|
Истощение ресурсов |
Р - количество населения; k - коэффициент пропорциональности; t - время. |
Общее решение:
частное решение: к 2112 году население Земли составит 40 миллиардов человек. |
|
Потеря заряда проводником |
Q - заряд проводника; t - время; k - коэффициент пропорциональности. |
Общее решение:
частное решение: при первоначальном заряде 1000 Кл через 10 минут заряд проводника будет 348,7 Кл. |
4. Первичное осмысление и закрепление связей и отношений в объектах изучения раздела «Дифференциальные уравнения». Студенты и преподаватель оценивают выступления докладчиков и по результатам их выступлений ставят баллы по заданным критериям (таблица 2, 3).
5. Подведение итогов занятия. Преподаватель подводит результаты и ставит оценку выполненным работам студентов.
Таблица 2
Критерии и показатели оценивания выступлений студентов (по Борисовой Н.В., Кузову В.Б.)
|
Критерии и показатели оценивания выступлений студентов |
|
|
Информативность доклада |
|
|
1 балл |
Доклад содержит отчет о проделанной работе, без описания возникавших сложностей и предпринимаемых для их решения действий. |
|
2 балла |
Доклад содержит отчет о проделанной работе, описание возникавших нештатных ситуаций и действий для их решения. |
|
3 балла |
Доклад содержит отчет о проделанной работе, описание возникавших нештатных ситуаций и действий для их решения; аналитическую часть - выводы относительно работы группы, рекомендации по ведению процесса с учетом выдававшихся заданий и т.д. |
|
Качество презентации |
|
|
1 балл |
На слайды вынесена малозначительная информация, содержание устного доклада слабо соотносится с содержанием слайдов. |
|
2 балла |
Содержание устного доклада соотносится с содержанием слайдов. На слайды вынесена вся значимая информация, однако не использовались средства визуализации информации (диаграммы, графики и т.д.). |
|
3 балла |
Содержание устного доклада соотносится с содержанием слайдов. На слайды вынесена вся значимая информация, при этом использовались средства визуализации информации (диаграммы, графики и т.д.) для её лучшего восприятия. |
|
Качество устного доклада |
|
|
1 балл |
Доклад сбивчивый, темп речи не выдерживается, информация на слух воспринимается сложно. Не используется профессиональная терминология. Имеет место «лишняя», малозначительная в контексте игры информация (о количестве неудачных попыток, сложности правильного выполнения действий, неудобстве программы-тренажера и т.д.). |
|
2 балла |
Устный доклад подготовлен, темп изложения – равномерный. Не используется профессиональная терминология. |
|
3 балла |
Доклад хорошо проработан, логически выверен, легко воспринимается, отсутствует «лишняя» информация; используется профессиональная терминология. |
Таблица 3
Критерии оценивания выполнения математических расчетов при решении задач естествознания
|
Баллы |
Критерии |
|
8-10 |
Четко сформулирована постановка задачи, составлена математическая модель задачи естествознания. Обоснованно получен правильный ответ. |
|
4-7 |
Ответ неверен, но решение содержит переход от исходной задачи к верному дифференциальному уравнению. |
|
0-3 |
Решение не соответствует ни одному из критериев, перечисленных выше. |
Результаты исследования и их обсуждение. В проекте приняли участие 17 из 20 студентов группы БО-18 с разным уровнем учебной подготовки. В процессе проектной деятельности студенты научились работать в команде, быть ответственными, распределять между собой обязанности. При изучении тем от них потребовались знания по математике и по физике. По окончании проекта у участников возник интерес к изучению математических методов при решении практико-ориентированных задач, произошло прочное усвоение нового материала, проявились творческие способности (при составлении презентаций), усилилось чувство ответственности. Контрольные работы по разделу «Дифференциальные уравнения» написали все 17 участников проекта (100%). Умение правильно использовать информацию, связывать между собой знания, полученные при изучении различных дисциплин, соотносить изученный материал с реальной жизнью – все это нашло воплощение в данном проекте.
Выводы. Таким образом, метод проектов помогает студентам еще глубже осознавать важность математического аппарата при описании различных процессов в природе. И в то же время способствует формированию навыков использования научного стиля в письменной речи, развивает творческие способности, навыки групповой коммуникации и техники публичных выступлений, воспитывает чувство ответственности.




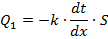
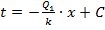 ;
;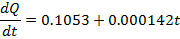
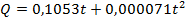 ;
;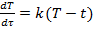
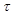 - искомое время охлаждения.
- искомое время охлаждения.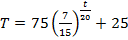 ;
;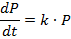
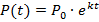 ;
;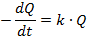
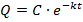 ;
;