Основными задачами инновационной деятельности учителя на уроках математики являются оптимизация учебного процесса, повышение эффективности усвоения знаний, умений и навыков, развитие алгоритмического мышления, способностей к математическому творчеству. Эффективность процесса обучения зависит от применения методов обучения. В последнее время в системе образования широкое распространение получили активные и интерактивные методы обучения.
Цель исследования: разработка методических рекомендаций по использованию активных и интерактивных методов обучения на уроках математики.
Материал и методы исследования
Выделяют следующие отличительные особенности активных методов обучения: активизация мышления, длительное время вовлечения обучаемых в учебный процесс, самостоятельное принятие решений, повышение мотивации, интерактивный характер [1].
В зависимости от наличия имитируемой деятельности активные методы обучения делят на два вида: имитационные и неимитационные. Выделяют два типа имитационных методов: игровые и неигровые [1].
Интерактивное обучение является одним из современных направлений развития активного обучения. Применение интерактивных методов связано с использованием средств информационных и коммуникационных технологий.
Выделяют следующие возможности информационных и коммуникационных технологий в обучении: быстрая обратная связь между пользователем и средствами информационных и коммуникационных технологий, визуализация учебной информации, моделирование, автоматизация процессов вычислительной деятельности и др. [2].
Формы и методы интерактивного обучения разделяют на следующие группы: дискуссионные, игровые, организационно-деятельностные игры, тренинговые формы проведения занятий [3].
В процессе обучения математике можно использовать различные виды активных и интерактивных методов обучения, в частности метод проектов и кейсы.
В процессе выполнения проектов деятельность школьников направлена на результат решения проблемы.
Выделяют три этапа выполнения проекта: организационно-подготовительный, технологический, обобщающий (рефлексивный) [4]. На первом этапе проводятся мотивация и целеполагание, а также планирование и принятие решений. На втором этапе происходит выполнение проекта. На третьем этапе проводятся защита проекта, проверка и оценка результатов.
Кейсы имеют некоторые особенности: в основе кейса лежит конкретная ситуация, при анализе кейса необходимо определить главную проблему, кейс может не иметь однозначного решения [1].
Выделяют пять этапов работы с кейсом.
1. На первом этапе происходит введение в кейс.
2. На втором этапе проводится анализ ситуации.
3. Третий этап – это этап презентации результатов.
4. На четвертом этапе проводится общая дискуссия.
5. На пятом этапе происходит подведение итогов [5].
Результаты исследования и их обсуждение
Рассмотрим в качестве примера проект для обучающихся 11-го класса «Пирамида», который является монопроектом, он практикоориентированный, с открытой координацией, внутренний, групповой, средней продолжительности.
Цель данного проекта: создание условий для обобщения и углубления знаний по теме «Пирамида». Задачи данного проекта: провести обобщение и систематизацию определений понятий, свойств понятий по рассматриваемой теме, составить или подобрать задачи с практическим содержанием, а также изучить исторические сведения.
Ученики работают по группам: первая группа собирает исторические факты, относящиеся к данной теме; вторая группа проводит обобщение и систематизацию определений и свойств понятий по рассматриваемой теме; третья группа проводит подбор практических задач или составляет практические задачи по данной теме. Затем проводится презентация результатов каждой группы и подводятся итоги.
В процессе организации проектной деятельности происходит развитие и воспитание обучающихся, педагогический процесс приобретает целостность.
В качестве примера рассмотрим кейс, который можно использовать на уроке математики в 6-м классе.
Кейс. Семья из трех человек (родители и ребенок в возрасте пяти лет), которая проживает в Омске, планирует отдых на море в городе Адлере. Возможные варианты поездки: на самолете, на поезде, на автомобиле. Используя соответствующие сайты, необходимо определить стоимость для каждого варианта, а также время, которое будет затрачено на дорогу. Какой вариант поездки будет наиболее выгодным для данной семьи?
Ученики делятся на три группы, каждая группа рассматривает один вариант поездки. Дается время на обсуждение, выдвигаются идеи. Учащиеся знакомятся с информацией, которая представлена на сайтах, и выбирают наиболее выгодный вариант для данной семьи. Применение кейсов на уроках математики способствует повышению мотивации, активизирует мышление учащихся.
В настоящее время актуальным является вопрос использования средств информационных и коммуникационных технологий в обучении математике с целью повышения эффективности усвоения знаний, умений и навыков. Для получения формулировок свойств понятий ученики самостоятельно могут производить с использованием средств информационных технологий построения разных графиков функций, геометрических фигур, измерять длины сторон, градусные меры углов, выполнять различные вычисления. Это способствует экономии времени на уроке, учебный материал приобретает более наглядный вид.
На уроках математики можно использовать программное средство Advanced Grapher, с помощью которого ученики могут строить графики линейных, квадратичных или других функций, проводить преобразования графиков, решать уравнения и системы уравнений графическим способом.
Рассмотрим пример. На этапе закрепления знаний по теме «Линейная функция» ученикам можно предложить выполнить следующие задания.
Задание 1. Найдите точки пересечения графиков функций аналитически и с помощью программы Advanced Grapher: у = x + 3 и у = 2x + 6.
Результат выполнения задания с использованием программы Advanced Grapher представлен на рисунке 1.
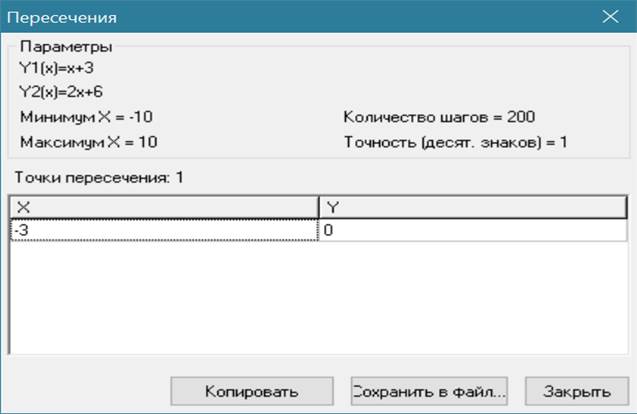
Рис. 1. Результат выполнения задания 1
Задание 2. Принадлежит ли точка М (36; –8) графику функции у = –2х + 4?
Результат выполнения задания с использованием программы Advanced Grapher представлен на рисунке 2.
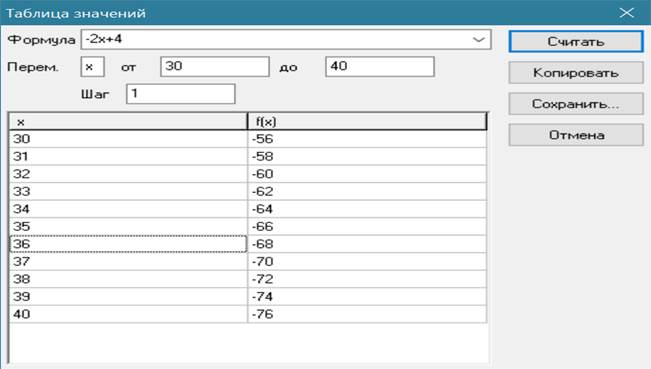
Рис. 2. Результат выполнения задания 2
Задание 3. Даны уравнения прямых: у = 3х – 4, у = 6 – 2х, у = 2х – 2.Имеют ли данные прямые общую точку?
Результат выполнения задания с использованием программы Advanced Grapher представлен на рисунке 3.
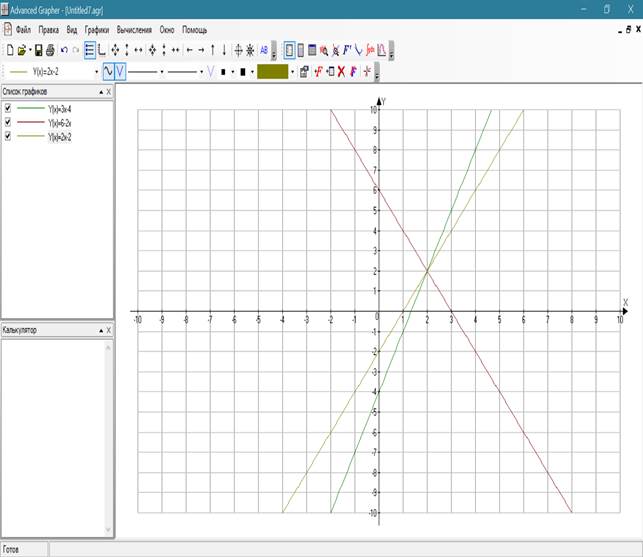
Рис. 3. Результат выполнения задания 3
При обучении учащихся геометрии можно использовать программное средство «Живая геометрия», с помощью которого ученики могут строить отрезки, окружности, прямые (перпендикулярные и параллельные); измерять длины отрезков, градусные меры углов и выполнять другие действия.
Например, при обучении теме «Центральные и вписанные углы» учащиеся с использованием программы «Живая геометрия» выполняют следующее задание (задание 4):
1. Начертите окружность.
2. Постройте две пересекающиеся хорды окружности.
3. Найдите длины отрезков хорд окружности.
4. Найдите произведение отрезков каждой хорды окружности.
5. Сравните полученные значения. Сделайте вывод.
Учитель координирует деятельность учащихся, разрешает возникающие трудности, оказывает помощь при выполнении заданий.
Возможный вариант выполнения задания представлен на рисунке 4.
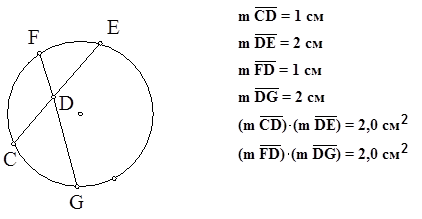
Рис. 4. Результат выполнения задания 4 с помощью программы «Живая геометрия»
Затем учитель предлагает ученикам начертить еще две пересекающиеся хорды и выполнить соответствующие задания. По завершении работы ученики сравнивают полученные значения и формулируют теорему о произведении пересекающихся хорд. Затем проводится доказательство теоремы.
При обучении теме «Соотношения между сторонами и углами треугольника» учащиеся с использованием программы «Живая геометрия» выполняют следующее задание (задание 5): построить произвольный треугольник и измерить длины всех его сторон. Затем необходимо найти суммы двух сторон и сравнить каждую сторону треугольника с суммой двух других сторон (рис. 5).
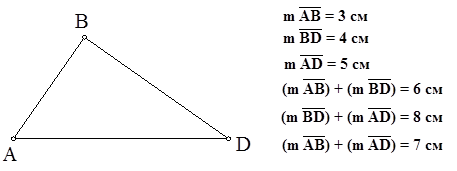
Рис. 5. Результат выполнения задания 5 с помощью программы «Живая геометрия»
Затем ученики изменяют положение вершин треугольника и выполняют соответствующие измерения и вычисления. В результате выполнения данного задания ученики могут самостоятельно сформулировать теорему «Неравенство треугольника». Затем проводится доказательство теоремы.
В процессе выполнения таких заданий ученики приобретают умения проводить наблюдение и сравнение объектов; в результате проведения эксперимента ученики могут выдвигать гипотезы, которые способствуют самостоятельной формулировке свойств понятий.
Заключение
Таким образом, применение активных и интерактивных методов в процессе обучения математике способствует оптимизации учебного процесса, повышению информативной емкости изучаемого материала, а также повышению эффективности усвоения математических знаний.



