Модернизация среднего математического образования, внедрение Федеральных государственных образовательных стандартов на современном этапе в центр всей учебно-воспитательной работы ставят личность ученика. Направленность на личность требует изменения методов обучения и воспитания, возникает необходимость максимально учитывать в процессе обучения индивидуальные особенности учащихся, развивать их творческие способности. Современное общество заинтересовано в том, чтобы выпускники могли самостоятельно и критически мыслить, видеть возникающие проблемы, активно действовать, принимать решения, гибко адаптироваться к изменяющимся условиям жизни, грамотно использовать информацию. Воспитание этих качеств личности возможно только в процессе творческой деятельности, одним из видов которой является поисковая деятельность. Применительно к процессу обучения поисковая деятельность трактуется как вид учебно-творческой деятельности, направленной на решение проблемных задач.
К числу характеристик творческих способностей учащихся относят следующие умения: 1) самостоятельно переносить знания в новые условия; 2) видеть новые проблемы в обычных условиях; 3) усматривать структуру проблемы или задания; 4) обнаруживать новую функцию знакомого объекта; 5) проявлять дальновидность в предсказании избранного пути решения проблемы; 6) комбинировать известные методы решения проблем для нахождения нового метода; 7) находить более изящный – точный, ясный, короткий способ решения при умелой опоре на уже известные способы и т. д. [1, с. 28]. В обучении математике эти умения формируются в процессе решения задач. Однако можно выделить ряд недостатков, относящихся к содержанию и методам решения задач, а также к методике обучения решению задач. Назовем лишь некоторые из них:
1) стандартизация методов решения задач, которая проявляется в стремлении решить со школьниками возможно большее число задач в ущерб их обучающему качеству;
2) обучение решению задач преимущественно по образцу; отсутствие целенаправленной работы учителя по формированию у школьников умения критически оценивать ход решения задачи и осуществлять проверку полученного результата;
3) очень мало задач в школьном курсе математики, решение которых подготовило бы школьников к деятельности, характерной для современного производства (рационализация и контроль, управление, изобретательство и т. п.), то есть к деятельности творческого характера; недостаточно также задач, в процессе решения которых было бы возможно формирование у школьников важнейших мыслительных умений (обобщать, анализировать, моделировать, осуществлять мысленный эксперимент и т. п.) [2, 3].
Между тем (как и ранее) в практике современного обучения математике на решение задач отводится большая часть учебного времени. Неэффективность его использования отрицательно сказывается на качестве обучения математике в целом. Это подтверждают и результаты ежегодно проводимых ОГЭ и ЕГЭ. В отчетах ФИПИ отмечаются главные причины ошибок выпускников при выполнении заданий ЕГЭ: недостаточные геометрические знания и графическая культура, неумение проводить анализ условия задачи, искать пути решения, недостаточная развитость наглядных геометрических представлений и т. д. [4, 5].
Одним из путей преодоления указанных выше недостатков и в то же время средством организации поисковой деятельности учащихся является использование геометрического метода в процессе решения алгебраических задач. Особенность геометрического метода, идущего от наглядных представлений, создает благоприятные возможности для формирования у учащихся таких профессионально значимых качеств, как пространственное воображение и логическое мышление. «Геометрический метод и есть не что иное, как живое воображение, в котором находят указания для логически проводимого решения», – отмечал академик А.Д. Александров [6, с. 61].
Как показывают практика и результаты нашего исследования, геометрические представления и геометрический метод играют большую роль в поиске решения алгебраических текстовых задач. Основная цель решения этих задач – познакомить учащихся с математическим моделированием, сформировать умения строить и исследовать простейшие математические модели. Представления о моделировании имеют для учащихся общекультурную и общеобразовательную ценность [7]. Поэтому текстовые задачи ежегодно бывают представлены в материалах ЕГЭ и ОГЭ. По последним данным ФИПИ с подобными задачами справились на профильном уровне 30% учащихся в 2017 году и 61% в 2018 году [4, 5]. Главной причиной возникающих трудностей является то, что процесс решения текстовых задач не поддается полностью алгоритмизации. Учащиеся изучают частные способы решения отдельных видов задач, которые скоро забываются ими, и, встретившись с задачей незнакомого или малознакомого вида, они не знают, как к ней подступиться, с чего начать решение. Поэтому необходимо формирование общего подхода к решению этих задач. Именно такой подход дает использование геометрического метода при поиске решения алгебраической задачи.
Цель исследования – разработать методику использования геометрического метода при поиске решения алгебраических текстовых задач.
Материал и методы исследования. В качестве материала исследования использовались текстовые задачи и методы их решения, содержащиеся в учебниках алгебры для 7–9-х классов, а также в материалах ОГЭ и ЕГЭ. В ходе исследования был осуществлен анализ научно-методической, психолого-педагогической и математической литературы, школьных учебников, материалов ОГЭ и ЕГЭ, интернет-источников; проводились наблюдение, беседа, эксперимент.
Результаты исследования и их обсуждение. Под геометрическим методом решения алгебраических задач мы понимаем метод решения, заключающийся в использовании геометрических представлений (изображений), законов геометрии и элементов аналитических методов (уравнений, систем уравнений, арифметических выражений и др.) [8, с. 5].
Итак, чтобы решить алгебраическую задачу геометрическим методом, необходимо:
1) построить геометрическую модель задачи; 2) составить числовое выражение или уравнение (систему уравнений), используя геометрические соотношения полученных фигур; 3) найти значение выражения или решения уравнения (системы уравнений); 4) исследовать полученное решение (выяснить, удовлетворяют ли корни уравнения условию задачи, исчерпывают ли они все решения задачи и т. д.).
Приведем примеры решения алгебраических задач разных типов геометрическим методом.
I. Задачи на движение без остановки
Как известно, в текстовых задачах рассматривается в основном равномерное движение. При равномерном движении пройденный путь равен произведению скорости и времени, поэтому его можно представить в виде площади прямоугольника, одна сторона которого изображает скорость, а другая – время, то есть в виде двумерной диаграммы. Использование двумерных диаграмм в решении алгебраических задач опирается на теорему о равновеликих прямоугольниках, приведем ее формулировку.
Теорема*. Если через произвольную точку Е диагонали АС прямоугольника ABCD (движение букв против часовой стрелки) проведены прямые 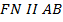 и
и 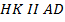 , то: 1) образовавшиеся прямоугольники
, то: 1) образовавшиеся прямоугольники 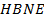 и
и 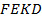 равновелики; 2) прямоугольники
равновелики; 2) прямоугольники  и
и 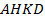 также равновелики, кроме того: 3) отрезки
также равновелики, кроме того: 3) отрезки 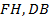 и
и 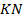 параллельны [9, с. 37].
параллельны [9, с. 37].
Рассмотрим примеры задач, при решении которых применяется эта теорема.
Задача 1. Из пункта А в пункт В, расстояние между которыми 33 км, одновременно выехали два велосипедиста. Один из них ехал со скоростью на 4 км/ч большей и прибыл в пункт В на 48 мин раньше другого. Сколько времени находился в пути каждый велосипедист?
Р е ш е н и е
1-й этап (построение двумерной диаграммы).
Пусть 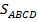 определяет путь, пройденный вторым велосипедистом (рис. 1).
определяет путь, пройденный вторым велосипедистом (рис. 1).
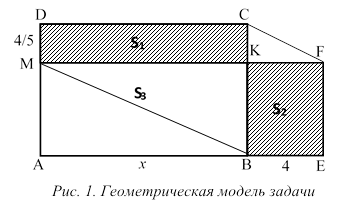
 .
.  – скорость второго велосипедиста (км/ч),
– скорость второго велосипедиста (км/ч),  – время его движения (ч).
– время его движения (ч).
Площадь 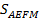 определяет путь, пройденный первым велосипедистом (км).
определяет путь, пройденный первым велосипедистом (км).
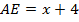 – скорость первого велосипедиста (км/ч),
– скорость первого велосипедиста (км/ч), 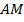 – время его движения (ч).
– время его движения (ч).
2-й этап (решение задачи с использованием геометрических соотношений).
Здесь возможно несколько способов.
1-й способ (используем равновеликость прямоугольников).
По условию задачи оба велосипедиста проехали одинаковый путь, поэтому
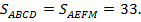
Исключая общую площадь 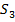 , получим:
, получим: 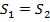 ,
, 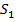 =
= 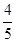 x,
x, 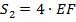 ,
,
где 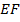 =
= 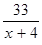 . В итоге получаем уравнение:
. В итоге получаем уравнение:
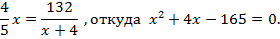
Решая уравнение, находим: 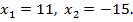 Второй корень данного уравнения не удовлетворяет условию задачи, поэтому
Второй корень данного уравнения не удовлетворяет условию задачи, поэтому 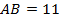 , тогда
, тогда 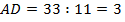 ,
, 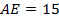 ,
, 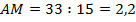 .
.
3-й этап (интерпретация полученного решения, перевод его на естественный язык).
О т в е т : первый велосипедист был в пути 2,2 ч, второй – 3 ч.
2-й способ (используем подобие треугольников).
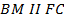 (по теореме*), поэтому
(по теореме*), поэтому 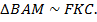 Из подобия треугольников следует:
Из подобия треугольников следует:
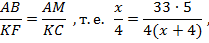
откуда после преобразований получим квадратное уравнение:
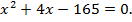
3-й способ (применяем свойства длины отрезка).
По условию задачи 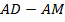 =
=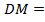
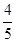 ,
, 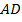 =
= 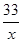 ,
, 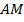 =
= 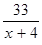 , поэтому получаем:
, поэтому получаем:
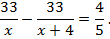
Такое же уравнение получается при решении задачи алгебраическим методом без чертежа. В итоге все три способа приводят к одному и тому же квадратному уравнению.
Среди задач на движение часто встречаются задачи на движение по реке. Большинство из них также можно решать геометрическим методом, включая в поиск решения не только алгебраические, но и геометрические знания учащихся. Приведем пример задачи этого типа.
Задача 3. Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км, а против течения 25 км. На путь по течению реки она затратила столько же времени, сколько на путь против течения. Какова скорость течения реки [10, с. 131]?
Алгебраический метод решения задачи приводит к дробно-рациональному уравнению
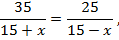
где 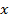 (км/ч) – скорость течения реки. Рассмотрим по этапам геометрический метод решения.
(км/ч) – скорость течения реки. Рассмотрим по этапам геометрический метод решения.
Р е ш е н и е
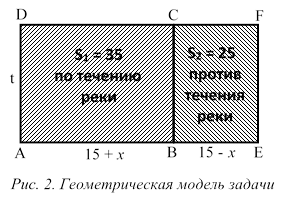 1-й этап (построение двумерной диаграммы).
1-й этап (построение двумерной диаграммы).
Пусть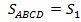 определяет расстояние, пройденное моторной лодкой по течению реки, а
определяет расстояние, пройденное моторной лодкой по течению реки, а  – расстояние против течения (рис. 2).
– расстояние против течения (рис. 2). 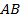 изображает скорость моторной лодки по течению реки, а
изображает скорость моторной лодки по течению реки, а 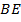 – скорость лодки против течения,
– скорость лодки против течения,  – время движения лодки по течению реки, причем
– время движения лодки по течению реки, причем 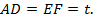 Обозначим скорость течения реки через
Обозначим скорость течения реки через 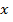 (км/ч), тогда
(км/ч), тогда 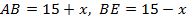 .
.
2-й этап (решение задачи с использованием геометрических соотношений).
Путь, пройденный лодкой по течению реки, равен: 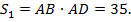
Путь, пройденный лодкой против течения реки равен: 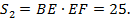
Площадь прямоугольника 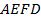 определяет все расстояние, пройденное моторной лодкой,
определяет все расстояние, пройденное моторной лодкой, 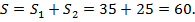
С другой стороны,
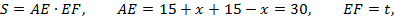
тогда имеем: 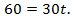 Получили линейное уравнение, решая его, находим
Получили линейное уравнение, решая его, находим 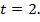
3-й этап (интерпретация полученного решения, перевод его на естественный язык).
Итак, 2 часа шла лодка по течению реки и столько же против течения. Тогда 35 : 2 = 17,5 (км/ч) – скорость лодки по течению реки; 17,5 – 15 = 2,5 (км/ч) – скорость течения реки.
О т в е т: 2,5 км/ч.
Рассмотренную задачу можно предложить учащимся на мотивационном этапе формирования геометрического метода решения алгебраических задач, так как геометрический метод приводит к линейному уравнению (задачу при этом можно решить даже в 7-м классе), а алгебраический – к дробно-рациональному уравнению. Кроме того, большую роль играет наглядность при поиске решения задачи.
II. Задачи на движение c остановкой
Задача 4. Поезд должен был пройти 54 км. Пройдя 14 км, он был задержан у семафора на 8 мин. Увеличив скорость после этого на 10 км/ч, он прибыл на место назначения по расписанию. Определите первоначальную скорость поезда [11, с. 149].
Р е ш е н и е
1-й этап (построение двумерной диаграммы).

Пусть  определяет весь путь, который должен пройти поезд (км) (рис. 3).
определяет весь путь, который должен пройти поезд (км) (рис. 3).
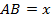 – скорость поезда по расписанию (км/ч),
– скорость поезда по расписанию (км/ч), 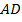 – время его движения (ч). Пусть
– время его движения (ч). Пусть 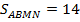 , а
, а 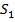 определяет путь, который прошел бы поезд за время стоянки.
определяет путь, который прошел бы поезд за время стоянки.
2-й этап (решение задачи с использованием геометрических соотношений).
За счет увеличения скорости на 10 км/ч поезд нагнал потерянное время, поэтому 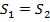 ,
, 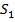 =
= 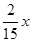 ;
; 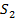 = 10 ×
= 10 × 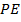 , но
, но 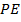 =
= 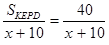 , поэтому
, поэтому 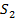 =
= 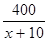 .
.
Так как  , то получаем уравнение:
, то получаем уравнение:
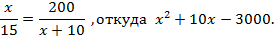
Решая данное уравнение, находим 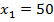 ,
, 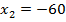 . Второй корень уравнения не удовлетворяет условию задачи, поэтому
. Второй корень уравнения не удовлетворяет условию задачи, поэтому 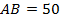 .
.
3-й этап. О т в е т: первоначальная скорость поезда 50 км/ч.
2-й способ (используем подобие треугольников).
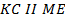 (по теореме*), поэтому
(по теореме*), поэтому 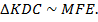 Из подобия треугольников следует:
Из подобия треугольников следует:
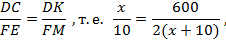
откуда после преобразований будем иметь:
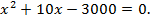
3-й способ (используем свойства длины отрезка).
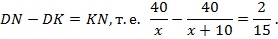
Такое же уравнение получается при решении задачи без чертежа.
В итоге все три способа приводят к одному и тому же квадратному уравнению, но разными путями. Учащиеся могут сравнить эти способы, выбрать из них наиболее рациональный.
III. Задачи на работу
Аналогично задачам на движение с помощью геометрического метода можно организовать и поиск решения задач «на работу» разными способами. Так как объем работы равен произведению производительности и времени, то его можно представить в виде площади прямоугольника, или двумерной диаграммы. Приведем пример.
Задача 5 (ЕГЭ, 2017). Плиточник должен уложить 187  плитки. Если он будет укладывать на 6
плитки. Если он будет укладывать на 6 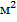 плитки в день больше, чем запланировал, то закончит работу на 6 дней раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
плитки в день больше, чем запланировал, то закончит работу на 6 дней раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Р е ш е н и е
1-й этап (построение двумерной диаграммы).
 Пусть площадь прямоугольника
Пусть площадь прямоугольника  определяет весь объем работы 187
определяет весь объем работы 187  плитки. Отрезок
плитки. Отрезок 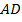 изображает производительность плиточника в день по плану (рис. 4),
изображает производительность плиточника в день по плану (рис. 4), 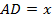 ;
; 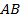 изображает количество дней, за которое он должен выполнить всю работу по плану.
изображает количество дней, за которое он должен выполнить всю работу по плану.
Если плиточник будет укладывать на 6 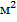 плитки в день больше, чем по плану, то следует прибавить к отрезку
плитки в день больше, чем по плану, то следует прибавить к отрезку 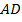 отрезок
отрезок 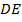 , условно изображающий 6
, условно изображающий 6 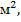 тогда
тогда 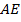 будет изображать повышенную производительность плиточника в день. Время его работы в этом случае
будет изображать повышенную производительность плиточника в день. Время его работы в этом случае 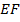 , а площадь прямоугольника
, а площадь прямоугольника 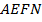 определяет весь объем работы.
определяет весь объем работы.
2-й этап (решение задачи с использованием геометрических соотношений).
Так как объем работы и в первом, и во втором случае один и тот же, то площади прямоугольников 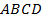 и
и 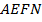 равны, поэтому по теореме*
равны, поэтому по теореме* 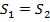 , или
, или
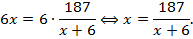
Учитывая, что 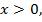 это уравнение равносильно следующему
это уравнение равносильно следующему
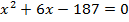 ,
,
откуда 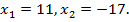 Второй корень отрицательный, поэтому он не удовлетворяет условию задачи. Итак,
Второй корень отрицательный, поэтому он не удовлетворяет условию задачи. Итак, 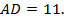
3-й этап (интерпретация полученного решения, перевод его на естественный язык).
Плиточник планирует укладывать в день 11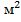 . О т в е т: 11
. О т в е т: 11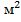 .
.
Аналогично рассмотренным задачам на движение, используя подобие треугольников 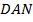 и
и 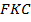 и свойства длины отрезка, можно найти еще два способа решения этой задачи.
и свойства длины отрезка, можно найти еще два способа решения этой задачи.
Мы рассмотрели задачи из курса алгебры 8-го класса и материалов ЕГЭ. Обучение решению задач с помощью двумерных диаграмм, как показал наш эксперимент, можно начинать уже в 7-м классе. В целях организации поисковой деятельности учащихся и учета их индивидуально-психологических и физиологических особенностей следует параллельно рассматривать решение задачи алгебраическим методом (без чертежа) и геометрическим методом, а впоследствии предоставлять учащимся право выбора метода решения алгебраической задачи.
Кроме двумерных диаграмм, в качестве геометрической модели задачи можно использовать иногда графическую модель. Графики равномерных процессов строятся при этом схематически (от руки), а затем используются свойства полученных геометрических фигур (равенство, подобие и т. д.). Приведем пример из курса алгебры 8-го класса.
Задача 6. Из 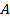 в
в 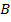 и из
и из 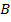 в
в 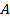 выехали одновременно два мотоциклиста. Первый прибыл в пункт
выехали одновременно два мотоциклиста. Первый прибыл в пункт 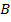 через 2,5 ч после встречи, а второй прибыл в пункт
через 2,5 ч после встречи, а второй прибыл в пункт 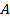 через 1,6 ч после встречи. Сколько часов был в пути каждый мотоциклист [10, с. 256]?
через 1,6 ч после встречи. Сколько часов был в пути каждый мотоциклист [10, с. 256]?
Эта задача в учебнике алгебры для 8-го класса отнесена к разделу «Задачи повышенной трудности». Алгебраический метод ее решения (без чертежа) приводит к уравнению
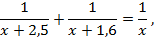
где 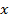 – время движения мотоциклистов до встречи, а единица – все расстояние между
– время движения мотоциклистов до встречи, а единица – все расстояние между 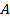 и
и 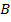 .
.
Рассмотрим геометрический метод решения по этапам.
Р е ш е н и е
1-й этап (построение графической модели).
Рассмотрим две прямоугольные системы координат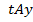 и
и 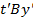 (рис. 5).
(рис. 5). 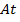 и
и 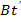 – оси времени с одинаковыми масштабами. Отрезок
– оси времени с одинаковыми масштабами. Отрезок  изображает расстояние между
изображает расстояние между  и
и  .
.
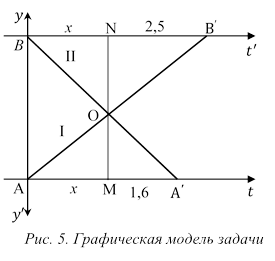 Так как движение равномерное, то отрезок
Так как движение равномерное, то отрезок 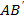 изображает график движения первого мотоциклиста, а отрезок
изображает график движения первого мотоциклиста, а отрезок 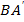 – график движения второго мотоциклиста. Пересечение графиков в точке
– график движения второго мотоциклиста. Пересечение графиков в точке 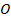 соответствует моменту их встречи.
соответствует моменту их встречи.
2-й этап (решение задачи с использованием геометрических соотношений).
Рассматривая две пары подобных треугольников (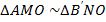 и
и 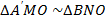 ), получим уравнение
), получим уравнение
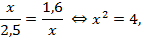
откуда 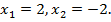 Второй корень не удовлетворяет условию задачи.
Второй корень не удовлетворяет условию задачи.
Итак, 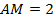 , тогда
, тогда 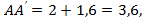
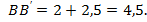
3-й этап (интерпретация полученного решения, перевод его на естественный язык).
Первый мотоциклист был в пути 4,5 ч, а второй – 3,6 ч.
О т в е т: 4,5 ч; 3,6 ч.
Геометрический метод, в отличие от алгебраического, позволяет иногда оригинально и быстро решить достаточно сложную задачу. Приведем пример.
Задача 7 (олимпиада «Ломоносов-2006») . Сын выбежал из школы в 17.00, через несколько минут отец вышел из дома в школу. Сын прибежал домой через 4 минуты после того, как отец вышел из дома. Отец пришел в школу в 17.10 того же дня. Какую часть пути сын пробежал до встречи с отцом? (Скорости отца и сына считать постоянными).
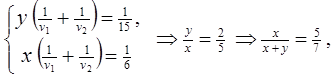 Алгебраический метод решения задачи (без чертежа) приводит к системе уравнений:
Алгебраический метод решения задачи (без чертежа) приводит к системе уравнений:
где x км прошел до встречи сын, а y км прошел до встречи отец.
Геометрический метод предполагает построение графической модели, аналогичной той, которая представлена на рисунке 5. Используя затем подобие треугольников, можно решить задачу, не составляя даже уравнения. Подробное решение показано в работе [12, с. 128].
Одно из преимуществ использования геометрического метода в решении текстовых задач перед алгебраическим методом состоит в наглядности. Геометрическая модель помогает не только понять смысл задачи, но и выявить скрытые зависимости между величинами, которые приводят к разным способам ее решения.
Заключение
Использование геометрического метода в алгебре направлено на реализацию деятельностного подхода в обучении математике, в частности на организацию поисковой деятельности учащихся в процессе решения задач. Построение геометрической модели позволяет сделать процесс, рассматриваемый в задаче, более осязаемым, визуальным. Кроме того, геометрический метод предоставляет возможность обучать разным методам рассуждений, сравнивать разные способы решения одной и той же задачи, проводить их оценку и выбирать наиболее рациональный из них. Учитель при этом может организовать дифференцированную работу с учащимися и учитывать их индивидуальные особенности, связанные с разными стилями мышления: понятийно-логическим и эмоционально-образным; кто-то может решить задачу алгебраическим методом, а кто-то геометрическим. Все это в целом способствует развитию обучающихся, формированию у них универсальных учебных действий.



