В профильный ЕГЭ по математике включены задания высокой сложности, требующие от школьников определенных знаний и умений. Для успешного решения таких задач необходимо не только знание стандартных алгоритмов, но и владение определенными элементами рассуждений, нестандартными навыками, умениями применять их при решении олимпиадных заданий.
Согласно спецификации контрольных измерительных материалов [1] задание № 19 относится к высокому уровню сложности части 2 экзамена, которая проверяет освоение математики на профильном уровне, необходимом для применения дисциплины в профессиональной деятельности, а также на творческом уровне. В частности, именно это задание проверяет умение строить и исследовать простейшие математические модели, поэтому традиционно вызывает наибольшие затруднения у выпускников как самое сложное задание экзамена. По крайней мере такое впечатление часто складывается в умах школьников, готовящихся к ЕГЭ. Учащиеся боятся даже браться за его решение, заранее настраивая себя на то, что оно им не по силам.
Учитывая вышесказанное, а также тот факт, что указанная задача часто связана со свойствами целых чисел, можно отметить необходимость более детального рассмотрения методики решения подобных задач с целью привлечения внимания к изучению элементарной теории чисел, содержащейся в школьных учебниках математики.
Цель исследования − проанализировать тематику задач № 19 профильного ЕГЭ по математике за разные годы, соотнести ее с содержанием школьных учебников по математике; выявить необходимый минимум знаний, связанных со свойствами целых чисел и необходимых для успешного решения указанной задачи.
Материал и методы исследования. Теория чисел − один из интереснейших разделов математики. Изучать его школьники начинают, как только переступают порог средней школы. На первом уроке математики в 5-м классе они знакомятся с таким понятием, как «натуральное число». Остальной материал из раздела теории чисел (числовые множества, понятие делимости, свойства делимости, простые числа, составные числа и т.д.) в школьном курсе математики дается в разных классах, то есть дискретно [2].
Анализ условий задачи № 19 за последние годы выявляет тесную связь с тематикой школьных учебников математики 5−6-х классов. Это десятичная запись целого числа и ее свойства, делимость целых чисел, свойства, признаки делимости; теорема о делении с остатком; простые и составные числа; разложение натуральных чисел в произведение простых множителей; сравнение чисел; приближение буквенной символики к записи условий задачи; проценты; среднее арифметическое целых чисел.
Указанный материал содержится, например, в учебниках 5-х классов [3, 4] и 6-х классов [5-7], включенных в Федеральный перечень учебников, рекомендованных к использованию в 2018–2019 уч. году, а также в пособиях [8-10].
Во всех анализируемых учебниках математики рассматриваются одни и те же темы в схожей последовательности, но с разной степенью подробности изложения. Например, в учебнике [4] изложены подробно с большим количеством интересных примеров и задач: понятие натуральных чисел, их десятичная запись, действия над ними. Далее вводится понятие дроби и действий над дробями, рассматриваются, в частности, десятичные дроби и действия над ними. Формулируются понятия среднего арифметического двух или нескольких чисел, процента от числа. В 6-м классе эти понятия углубляются и расширяются на множество целых и рациональных чисел. Изложение в учебнике [5] для 6-го класса завершается решением линейных уравнений и задач с помощью уравнений.
Этих сведений из программы по математике для 5−6-х классов вполне достаточно, чтобы решить некоторые типы задач № 19 ЕГЭ по математике.
Задание № 19 состоит из трех пунктов, условия которых чаще всего связаны с целыми числами и их свойствами. Самый легкий пункт а), который в некоторых случаях решается с помощью конструкции соответствующего числового примера; пункт б) сложнее, и самый сложный − пункт в), при решении которого обычно полезны результаты решений а) и б).
Пример 1 [11] Про натуральное число Р известно, что сумма трех его наименьших натуральных делителей равна 8.
а) Найдите число Р, у которого сумма трех наибольших натуральных делителей равна 289.
б) Может ли сумма трех наибольших натуральных делителей числа Р равняться 255?
в) Найдите все возможные числа Р, у которых сумма трех наибольших натуральных делителей не превосходит 100.
Рассмотрим далее решение, которое мог бы осуществить ученик при достаточной подготовке, используя только материал 6-го класса.
Наименьшим натуральным делителем числа 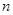 является 1, и значит, если
является 1, и значит, если 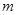 и
и 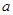 − два другие наименьшие натуральные делители, то это простые числа. По условию
− два другие наименьшие натуральные делители, то это простые числа. По условию 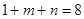 , т. е.
, т. е. 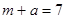 . Значит,
. Значит, 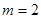 ,
, 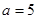 . Тогда набольшие натуральные делители числа
. Тогда набольшие натуральные делители числа 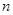 есть
есть 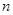 ,
, 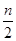 ,
,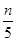
 и
и 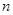 делится на 10 и не делится на 3. По условию пункта а) имеем равенство
делится на 10 и не делится на 3. По условию пункта а) имеем равенство 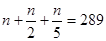 , приводя которое к общему знаменателю, имеем
, приводя которое к общему знаменателю, имеем 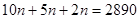 , откуда
, откуда  , а после деления на 17 получаем
, а после деления на 17 получаем 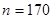 .
.
Мы видим, что решение пункта а) вполне доступно ученику, хорошо усвоившему тему делимости целых чисел в 6-м классе.
Имея план решения пункта а) и ключевое замечание, что 3 не делит 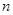 , без труда решаем пункт б). По условию
, без труда решаем пункт б). По условию 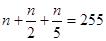 . Упрощаем:
. Упрощаем:  ,
, 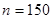 , но 150 делится на 3, поэтому не существует искомого натурального числа
, но 150 делится на 3, поэтому не существует искомого натурального числа 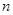 , удовлетворяющего условиям пункта б).
, удовлетворяющего условиям пункта б).
Аналогично решаем пункт в). По условию 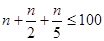 , после упрощений
, после упрощений 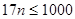 , откуда после деления на 17 имеем
, откуда после деления на 17 имеем 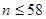 . Так как
. Так как 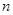 делится на 10 и не делится на 3, то перебором получаем
делится на 10 и не делится на 3, то перебором получаем 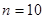 или
или 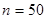 . Ответ: а) 170; б) нет; в) 10 или 50.
. Ответ: а) 170; б) нет; в) 10 или 50.
Очень поучительная задача! При ее решении большую роль играют логические рассуждения. Следующий пример немного сложнее.
Пример 2 [12]. По кругу в некотором порядке по одному разу написаны числа от 9 до 18. Для каждой из десяти пар соседних чисел нашли их наибольший общий делитель.
а) Могло ли получиться так, что все наибольшие общие делители равны 1?
б) Могло ли получиться так, что все наибольшие общие делители попарно различны?
в) Какое наибольшее количество попарно различных наибольших общих делителей могло при этом получиться?
Решение. а) Путем проб и ошибок, учитывая три простых числа 11, 13, 17, можно построить искомую последовательность чисел 9, 10, 11, 18, 13, 12, 17, 14, 15, 16; если переставлять в этой последовательности местами простые числа 11, 13, 17, то получим еще пять других искомых последовательностей чисел.
б) Этот пункт решается с помощью простого рассуждения: всего по кругу записывается 10 чисел, для каждой пары соседних чисел мы ищем наибольший общий делитель, поэтому получаем 10 наибольших общих делителей. Если бы они были все попарно различны, то хотя бы один из них был не меньше числа 10, но так как наибольший возможный общий делитель НОД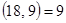 , то удовлетворить условиям пункта б) невозможно.
, то удовлетворить условиям пункта б) невозможно.
в) Заметим, что 11, 13, 17 − все простые числа между числами 9 и 18. Наибольшие общие делителем этих чисел c соседними равны 1. Следовательно хотя бы четыре из всех десяти наибольших общих делителей равны 1. Поэтому не может быть больше, чем семь попарно различных наибольших общих делителей, при любой расстановке по кругу чисел 9, 10, 11, 12, 13, 14, 15, 16, 17, 18. Искомая расстановка: если по кругу расположить числа в таком порядке: 9, 18, 12, 16, 14, 13, 11, 17, 10, 15, то получим ровно семь попарно различных наибольших общих делителя. Ответы: а) Да; б) Нет; в) Семь.
На математических олимпиадах и в условиях ЕГЭ по математике нередко формируются задачи на делимость, связанные с десятичным представлением чисел.
Пример 3 [13]. Дано трехзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 90?
б) Может ли частное этого числа и суммы его цифр быть равным 88?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Решение. Пусть данное число равно 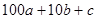 , где
, где 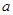 ,
, 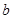 ,
, 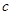 − цифры соответственно сотен, десятков и единиц. Если частное этого числа и суммы его цифр равно
− цифры соответственно сотен, десятков и единиц. Если частное этого числа и суммы его цифр равно 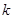 , то
, то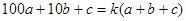 , т. е.
, т. е. 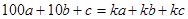 .
.
а) Если частное 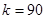 , то
, то 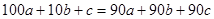 , откуда
, откуда 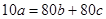 . Из этого равенства следует, что 10 делит с, следовательно,
. Из этого равенства следует, что 10 делит с, следовательно, 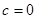 , поскольку
, поскольку 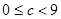 , поэтому
, поэтому 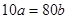 , т.е.
, т.е. 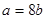 и значит
и значит 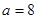 ,
, 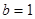 . Таким образом, единственное трехзначное число 810 удовлетворяет условию пункта а).
. Таким образом, единственное трехзначное число 810 удовлетворяет условию пункта а).
б) Если частное 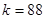 , то
, то 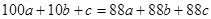 , откуда
, откуда 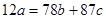 . Из предыдущего равенства следует, что 6 делит
. Из предыдущего равенства следует, что 6 делит 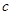 , т.е.
, т.е. 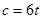 , и тогда
, и тогда 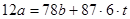 . Сокращая обе части последнего равенства на 6, получаем
. Сокращая обе части последнего равенства на 6, получаем 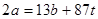 , очевидно, это уравнение не имеет решений при
, очевидно, это уравнение не имеет решений при 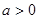 ,
, 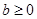 ,
, 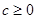 , поскольку
, поскольку 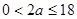 .
.
в) Пусть 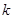 − наибольшее натуральное значение частного от деления
− наибольшее натуральное значение частного от деления 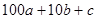 на
на 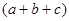 и делимое не кратно 100. Тогда
и делимое не кратно 100. Тогда 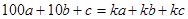 . После упрощения
. После упрощения 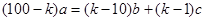 . Учитывая, что
. Учитывая, что 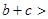 и
и 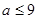 , получаем неравенства
, получаем неравенства 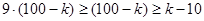 , откуда
, откуда 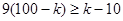 ,
, 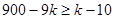 , и значит,
, и значит, 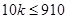 , что влечет
, что влечет 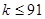 . Далее частное при делении 910 на сумму его цифр (9+1+0) равно 91 − максимальному возможному значению. Ответы: а) да; б) нет; в) 91.
. Далее частное при делении 910 на сумму его цифр (9+1+0) равно 91 − максимальному возможному значению. Ответы: а) да; б) нет; в) 91.
Пункт а) и даже пункт б) вполне доступны для решения учащимся и снова опираются на материал 6-го класса.
В 9-м классе изучают арифметическую и геометрическую прогрессии, их также используют в задачах № 19, предполагая, что их члены натуральные или целые числа.
Пример 4 [14]. Даны 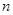 различных натуральных чисел, составляющих арифметическую прогрессию (
различных натуральных чисел, составляющих арифметическую прогрессию (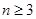 ).
).
а) Может ли сумма данных чисел быть равной 10?
б) Каково наибольшее значение n, если сумма всех данных чисел меньше 1000?
в) Найдите все возможные значения n, если сумма всех данных чисел равна 129.
Решение. Без ограничения общности можно считать, что числа составляют возрастающую арифметическую прогрессию. Пусть 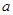 − первый член этой прогрессии, а
− первый член этой прогрессии, а 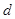 − ее разность. Тогда сумма
− ее разность. Тогда сумма 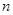 членов равна
членов равна 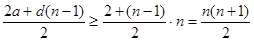 . Поэтому должно быть
. Поэтому должно быть 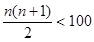 , и мы приходим к квадратичному неравенству
, и мы приходим к квадратичному неравенству 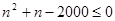 , откуда корни
, откуда корни 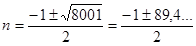 , и значит,
, и значит, 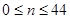
 Сумма арифметической прогрессии 1, 2, 4, …, 44 равна
Сумма арифметической прогрессии 1, 2, 4, …, 44 равна 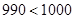 . Значит, наибольшее значение
. Значит, наибольшее значение 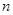 равно 44.
равно 44.
Для суммы членов арифметической прогрессии, удовлетворяющей условно в), верно: 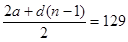 , т.е.
, т.е. 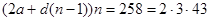 . Таким образом, число
. Таким образом, число 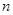 , являясь делителем 258, может принимать (учитывая, что
, являясь делителем 258, может принимать (учитывая, что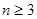 ) лишь значения 3, 6, 43, 86, 129, 258. Если
) лишь значения 3, 6, 43, 86, 129, 258. Если 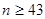
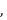 то
то 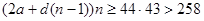
 следовательно,
следовательно, 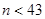
 Так как по условию
Так как по условию 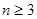 , то возможно лишь
, то возможно лишь 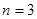 или
или 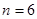 . Оба случая реализуются: арифметические прогрессии с 3 и 6 членами с суммой 129 существуют, например 42, 43, 44 и 19, 20, 21, 22, 23, 24. Ответы: а) да; б) 44; в) 3, 6.
. Оба случая реализуются: арифметические прогрессии с 3 и 6 членами с суммой 129 существуют, например 42, 43, 44 и 19, 20, 21, 22, 23, 24. Ответы: а) да; б) 44; в) 3, 6.
Анализируя материал, связанный со свойствами натуральных и целых чисел в школьных учебниках и условиях задачи № 19, замечаем, что на дополнительных занятиях по математике, или в школьных кружках, или при подготовке к ЕГЭ учащийся должен расширить и углубить свои знания, относящиеся к числам. Важно, например, для нахождения НОД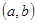 целых чисел
целых чисел 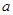 и
и 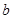 научиться использовать алгоритм Эвклида. Из канонического представления натурального числа
научиться использовать алгоритм Эвклида. Из канонического представления натурального числа 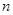 в произведение простых множителей
в произведение простых множителей 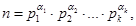
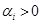 ,
, 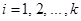 вытекает, что делители числа
вытекает, что делители числа 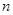 имеют вид
имеют вид 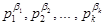 , где
, где 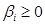 ,
, 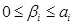 ,
, 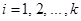 , а также что число
, а также что число 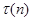 различных натуральных делителей числа n вычисляется по формуле [15, стр. 2]:
различных натуральных делителей числа n вычисляется по формуле [15, стр. 2]:
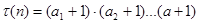 .
.
Основное свойство простых чисел, связанных с делимостью: если простое число 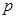 делит произведение целых чисел
делит произведение целых чисел 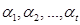 , то
, то 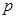 делит по крайне мере один из сомножителей
делит по крайне мере один из сомножителей 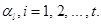 Единственное четное простое число – это 2. Полезно также помнить первые 24 простых числа: 2, 3, 5, 7, …, 97. Справедливо также, что если натуральное число
Единственное четное простое число – это 2. Полезно также помнить первые 24 простых числа: 2, 3, 5, 7, …, 97. Справедливо также, что если натуральное число 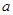 не делится ни на одно из простых чисел, не превосходящих
не делится ни на одно из простых чисел, не превосходящих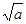 , то
, то 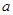 − простое. По теореме о делении с остатком при целом
− простое. По теореме о делении с остатком при целом 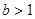 любое натуральное число
любое натуральное число 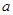 можно единственным образом представить в виде
можно единственным образом представить в виде 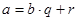 , где
, где 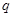 ,
, 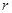 – целые числа
– целые числа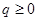 ,
, 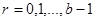 [10]. Желательно знать метод математической индукции, с его помощью можно доказать, например, что произведение любых
[10]. Желательно знать метод математической индукции, с его помощью можно доказать, например, что произведение любых 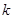 последовательных целей чисел делится на
последовательных целей чисел делится на 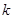 (и даже на
(и даже на 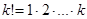 ) без остатка [10]. Для вычисления НОК
) без остатка [10]. Для вычисления НОК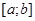 удобно использовать формулу
удобно использовать формулу
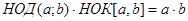 .
.
Необходимо также знать, что если 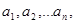
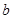 − целые числа, то уравнение
− целые числа, то уравнение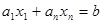 имеет решения в целых, только если
имеет решения в целых, только если 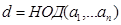 делит
делит 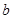 . В частности, уравнение
. В частности, уравнение 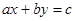 при целых
при целых 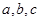 имеет решение в целых числах, только если
имеет решение в целых числах, только если 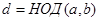 делит
делит 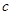 . При этом множество всех решений этого уравнения можно представить в форме
. При этом множество всех решений этого уравнения можно представить в форме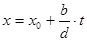 ,
,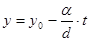
 где
где 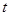 – пробегает все целые числа;
– пробегает все целые числа; 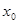 ,
, 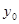 – частое решение этого уравнение, т.е.
– частое решение этого уравнение, т.е. 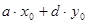 [10].
[10].
Результаты исследования и их обсуждение. Нами приведен минимум фактов, связанных с делимостью целых чисел и необходимых для решения последней задачи ЕГЭ. Более общим образом ученик должен стремиться научиться хорошо вычислять без калькулятора задачи и с целыми числами, и с дробями, и с действительными числами по всем темам школьного курса математики не только для успешной сдачи ОГЭ или ЕГЭ по математике, но и для успешной учебы в вузе и в своей последующей деятельности.
Заключение. Можно заключить, что тематика условий задач № 19 ЕГЭ по математике разнообразна, но она опирается на материал школьного курса математики и нередко не выходит даже за пределы программы по математике для 5–9-х классов. Особенно просто решается обычный пункт а) задачи № 19, решение которого иногда доступно даже ученику 6-го класса.
Тем не менее задача № 19 имеет в целом творческий характер и требует при решении изобретательность, логических рассуждений и числовой культуры. Поэтому учителю математики надо разъяснить школьником особенности задачи № 19 и сообщать круг фактов и умений, который позволяет ее успешно решить.



