Преподаватели технических вузов нередко сталкиваются с проблемой поиска новых подходов в образовании. Современный студент – человек творческий, свободный, легко ориентирующийся в сети Интернет, в связи с этим не очень трудолюбивый. Преобладание традиционного подхода, при котором главным является передача знаний от преподавателя к учащемуся, зачастую приводит к формированию пассивной аудитории, не готовой слушать и воспринимать информацию. Тем более, говоря о студентах первого курса технического вуза, можно предположить, что трудности обучения связаны еще и с проблемой перехода с одной ступени образования на другую. Высшая математика в техническом вузе занимает вполне определенное положение. Студент любого технического вуза знает, что в основе всех его специальных технических предметов лежит серьезный курс высшей математики и что поэтому без знания высшей математики инженера из него не выйдет.
Целью нашего исследования является изучение педагогического опыта преподавания высшей математики и моделирование процесса математического образования студентов в период обучения на первом курсе технического вуза на примере Московского государственного университета «Станкин».
Сформулируем общие проблемы обучения [1]:
- несоответствие между увеличением объема учебной информации и фактором ограниченного времени обучения;
- интенсификация образовательного процесса;
- проблема формирования и активизации познавательных интересов учащегося;
- проблема целостного формирования личности.
Но в результате нашего исследования мы выявили также следующие проблемы:
- проблема доминанты алгоритмического мышления;
- ученический формализм в обучении;
- межпредметная раскоординированность учебного процесса;
- отсутствие достаточной мотивации к получению новых знаний;
- несоответствие дидактических целей высшего технического образования целям, сформулированным учащимся на основе здравого смысла (опыта учащегося).
Для решения указанных проблем, а также для облегчения процесса адаптации в вузе и для упрощения процесса обучения во многих вузах, в частности в МГТУ «Станкин», создана электронная образовательная среда, в которой размещены материалы по предметам в электронном виде: рабочие программы дисциплин, конспекты лекций, методические указания для обучающихся, электронное тестирование и многое другое, что позволяет упростить процесс самостоятельной работы студента. В то же время в процессе аудиторной работы преподаватель должен найти приемы, которые позволят улучшить восприятие той или иной информации. В вузе процесс обучения отличается более осознанным подходом к будущему знанию (прагматический мотив), но само обучение, кроме навыков, полученных в средней школе, требует развития качества самоанализа, самоидентификации изменяющейся среде. Подходя к процессу обучения как к системе, организующей мышление, память, внимание, мы в нем выделяем решение задач, сформулированных в любой форме [2].
Когнитивная деятельность в процессе решения задач в вузовской среде имеет весьма широкие границы: от сбора информации об оборудовании и проведения эксперимента до теоретико-философских обобщений результатов в абстрактных и технических науках. Следовательно, мотивированная активность связана с приобретением, организацией и использованием знания. Решение задач в математике обладает одним из самых главных преимуществ – возможностью моделировать процесс мышления, формализовать способ решения, иметь акт эксперимента в виде решения, представленного самим испытуемым. Рассматривая процесс поиска студентами решения определенной математической задачи, можно обнаружить, что сложность состоит не только в отсутствии знаний, но и в неумении их извлекать и применять [3, c. 206].
На примере темы «Интегральное исчисление» попробуем проанализировать подход к систематизации знаний. Интегрирование функций является отличной основой для развития творческой деятельности через самостоятельную работу.
По окончании изучения различных методов интегрирования нередко студент не в состоянии понять, какой метод в каком случае применяется. Для систематизации методов интегрирования студентам предлагается найти отличия в решении следующих примеров [4]:
1) 
;
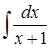2) 
;
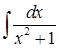3) 
;
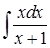4) 
;
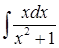5) 
;
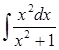6) 
.
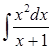На первый взгляд при невнимательном рассмотрении студенты говорят, что эти примеры мало чем отличаются и выглядят не очень сложно. Но в процессе решения учащемуся приходится вспомнить не только таблицу интегралов (пример 2), но и применить методы, изученные ранее: свойства дифференциала (пример 1), подведение под знак дифференциала (пример 4), интегрирование неправильных рациональных дробей (примеры 3, 5, 6).
Здесь рассмотрим подробнее решение примера 3. Нередко можно заметить, что студенты указанную задачу решают разными способами:
Способ 1. Выделение целой и дробной части
;
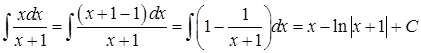Но иногда видим, что студент делает замену переменной:
Способ 2.
.
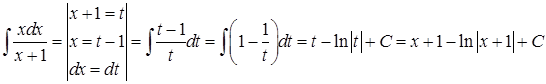Второй способ хоть и громоздкий, все же требует задействования более сложных навыков: здесь требуется грамотно ввести замену и перейти обратно к исходной переменной.
На следующем занятии к этим примерам можно добавить следующие для установления отличий [5]:
7) 
;
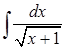8) 
;
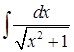9) 
;
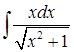10) 
.
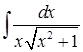Если первые шесть интегралов могут особых проблем и не вызвать, а лишь помочь структурировать методы интегрирования, помочь прочувствовать различия применения подходов к решению, то интегралы с 7-го по 10-й уже имеют своей целью выбор оптимального способа решения, тем более у учащихся чаще всего присутствует страх перед иррациональностью. И если интегралы 7 и 8 еще достаточно просты (хотя имеет место проблема, когда студент сделал огромные преобразования, в процессе которых пришел к интегралам типа 7 и 8, и не может сообразить, что делать дальше), то интегралы 9 и 10 требуют задействования многих механизмов мышления.
Остановимся подробнее на примере 10. Как известно, существует несколько способов решения подобного примера, и здесь студенту предлагается выбор.
Способ 1. Подстановка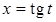 
, в таком случае, пользуясь тригонометрической формулой 
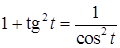, получим, что 
, 
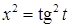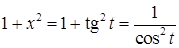, откуда 
, 
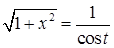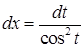. В итоге имеем:
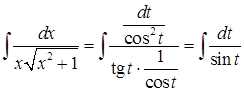, полученный интеграл можно решить с помощью универсальной тригонометрической подстановки. Весь описанный способ очень трудоемкий, необходима двойная замена, вернуться к исходной переменной сложно, не зная соответствующих формул.
Способ 2. Подстановка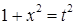 
. Тогда 
, 
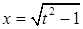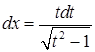. В итоге имеем:
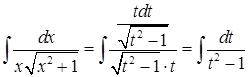. С помощью такой замены получили табличный интеграл, решение получилось более коротким, но тем не менее нужно вернуться к исходной переменной, а это также может представлять трудность.
Способ 3. Вынесение из-под знака корня x и внесение под знак дифференциала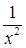 
. В итоге имеем:
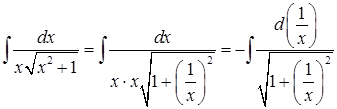. Сделав замену 
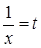, придем к интегралу 8. Проблемы могут возникнуть на этапе преобразований.
Если дать возможность прорешать этот пример всеми способами, рассмотреть поподробнее все возникающие в процессе решения проблемы, можно избежать сложностей в будущем.
Здесь еще рассмотрим пример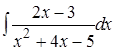 
. Предложим решить его студенту разными способами [6].
Способ 1. Разложим знаменатель на множители:
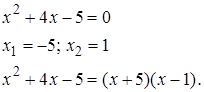
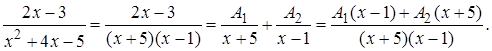
Приравняем числители левой и правой дробей, получим
.
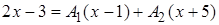При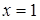 
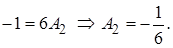
При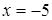 
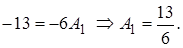
То есть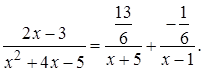 
Вернемся к интегралу:
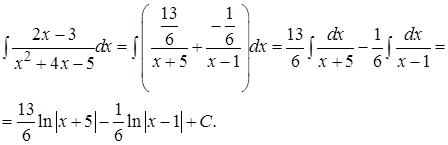
Способ 2. Выделим в числителе производную знаменателя
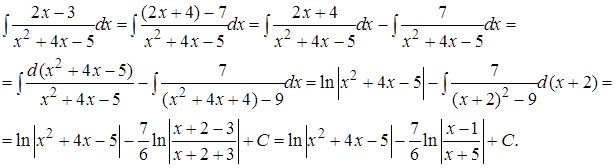
Заметим, что в процессе решения любым из способов мы приходим в процессе преобразований к интегралам типа 1–6.
Неизбежны трудности и при интегрировании тригонометрических выражений. Здесь тоже полезно использовать несколько способов решения одного и того же задания [7].
Например, рассмотрим интеграл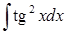 
.
Способ 1. Применение школьных тригонометрических формул:
.
Способ 2. Подстановка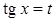 
, тогда 
, 
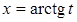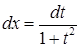. В итоге имеем:
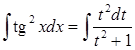, а это интеграл номер 5.
Предлагая студенту на выбор один из способов, мы развиваем не только математическое мышление, но и творчество, необходимое для жизни в целом. Суть указанных примеров в том, чтобы студент видел перед глазами функциональную систему действий, смог указать последовательность их выполнения, тренировать умственную и речевую формулировки. Тем самым формируется организация последовательности действий и структуры результата. Исследовательские навыки, полученные в курсе математического анализа, оказывают положительное влияние на характер всей учебной деятельности обучающегося.
Таким образом, мы видим, что при установлении разницы между интегралами типа 1–6 студент может избежать трудностей при решении примеров типа 7–10, а также находить новые способы решения поставленных задач [8].
В результате использования описанной систематизации методов интегрирования существенно повышаются математическая грамотность студентов, качество формирования логического мышления. Практическая реализация указанных методов позволяет воспитать более качественного специалиста.