Инсульт является одной из ведущих медико-социальных и экономических проблем, требующих пристального внимания как со стороны клиницистов, так и исследователей. Особенностью данного заболевания является то, что даже при благоприятном исходе большая часть больных уже не могут вернуться к прежнему образу жизни [1; 2]. Особое внимание в аспекте данной проблемы уделяется разработке и внедрению прогностических моделей исходов инсульта [3]. Актуальность прогнозирования инсульта продиктована необходимостью быстрой оценки тяжести инсульта, что способствует правильному решению при выборе оптимальной тактики введения больного [4]. И создает предпосылки для разработки профилактических мер по предупреждению повторного инсульта [5].
В настоящее время в неврологии уже предложено и успешно используется большое количество прогностических моделей, касающихся острого периода инсульта [6; 7]. При этом практически не представлено исследований, посвященных разработке прогностических моделей вероятности отдаленного летального исхода инсульта. Также важно отметить, что инсульт является многофакторным заболеванием, и глубокий анализ всех значимых предикторов летального исхода инсульта имеет важное значение для построения прогностической модели с высоким процентом чувствительности и специфичности.
Цель исследования: разработать комплексную прогностическую модель вероятности летального исхода инсульта на основании анализа статистически значимых предикторов летального исхода инсульта.
Материалы и методы исследования. Исследование выполнено с использованием данных, полученных методом территориально-популяционного регистра из шестнадцати регионов РФ с 2009 по 2016 г. среди населения 25 лет и старше (Ивановская, Свердловская, Иркутская, Сахалинская, Архангельская, Оренбургская, Воронежская, Рязанская, Белгородская области; республики Башкирия, Татарстан, Дагестан, Карелия, Саха и Алтайский край). Все анализируемые предикторы летального исхода инсульта были документально подтверждены в медицинских картах. Стресс как предиктор летального исхода регистрировали, если пациент на момент развития инсульта постоянно или длительным курсом принимал психотропные препараты и это было документировано. Всего было выявлено 50 902 случая инсульта (мужчин 48%, женщин 51,92%), из которых было исключено 1553 случая (3,05%), у которых отсутствовали полные данные о факторах риска инсульта.
Статистический анализ проводился с использованием языка программирования статистических расчетов R версии 3.3.2. Для каждого анализируемого предиктора летального исхода инсульта рассчитывали отношение шансов (OR – odds ratio). Анализ зависимостей исхода инсульта от предикторов проводился с использованием однофакторной логистической регрессии и последующим построением кривых оценки качества бинарных классификаций с расчетом отношения шансов. Построение дерева решений осуществлялось с помощью методики LOTUS [8]. При создании прогностической модели использовали критерий согласия Хосмера-Лемешова (значение критерия χ2=3,17, число степеней свободы (df) =8, уровень p для критерия=0,9232). На узлах применяли множественную логит–регрессию с пошаговым выбором показателей. Уровень статистической значимости p для входа показателя в модель по результатам был равным 0,049. Чувствительность прогностической модели составила 73,84%, специфичность 70,50%.
Результаты исследования и их обсуждение. На основе анализа 47796 случаев инсульта были выявлены статистически значимые предикторы летального исхода инсульта в анализируемой популяции: подтвержденный диагноз субарахноидального или внутримозгового кровоизлияний; диагноз неуточненный инсульт (неуточненный как кровоизлияние или инфаркт мозга) (OR в пределах 2-4); заболевания сердца; фибрилляция предсердий; возраст больного на момент развития инсульта (OR в пределах 1,5-2); наличие сахарного диабета (СД), инсульта в анамнезе, наличие фактора стресса, женский пол (OR в пределах 1,05-1,35); использование методов нейровизуализации (КТ/МРТ), диагноз ишемический инсульт и мужской пол характеризовались обратной связью с исходом инсульта.
Далее по результатам анализа статистически значимых предикторов летального исхода инсульта была создана прогностическая модель (дерево решений) на основе 18117 случаев инсульта (больные инсультом, которые имели все предикторы, выбранные для построения модели) (рисунок).
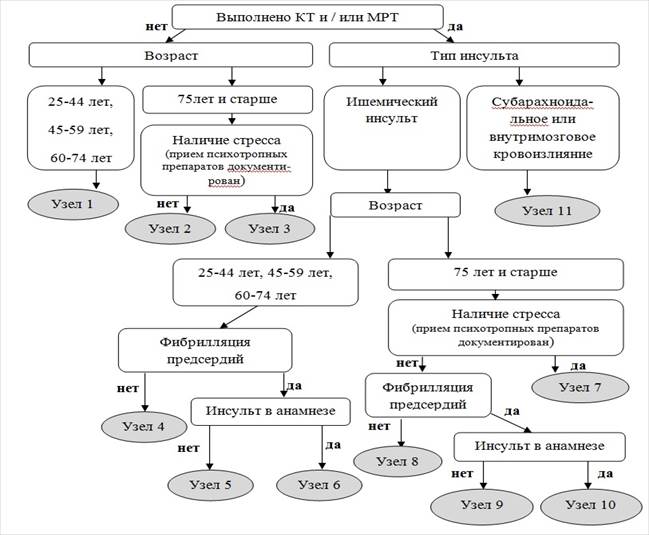
Схематическое изображение дерева решений (методика LOTUS)
Движение по схеме должно осуществляться сверху вниз, начиная с факта выполнения больному КТ/МРТ. На каждом узле дерева оценивается наличие определенного предиктора, в результате чего каждый больной попадает на один из терминальных узлов. На каждом терминальном узле возможен расчет вероятности летального исхода инсульта с использованием регрессионного уравнения зависимости (для выведения регрессионного уравнения зависимости для каждого терминального узла нами производился расчет регрессионного коэффициента и значения OR).
В таблице 1 представлена характеристика первого терминального узла дерева решений.
Таблица 1
Характеристика терминального узла 1 дерева решений
|
Узел 1 |
|||
|
Переменная |
Регрессионный коэффициент |
OR для коэффициента |
Уровень значимости p для коэффициента |
|
Свободный член |
-1,8837 |
– |
0,000018 |
|
Возраст |
0,0246 |
1,0249 |
0,000789 |
|
Заболевания сердца |
0,3010 |
1,3512 |
0,030035 |
Как видно из таблицы 1, вероятность летального исхода будет увеличиваться в 1,02 раза с увеличением возраста на каждый год жизни и в 1,35 раза при наличии заболевания сердца. Уравнение зависимости для данного узла имеет следующий вид: вероятность исхода = exp(-1,8837 + 0,0246*Возраст + 0,3010* Наличие заболеваний сердца) / (1+ exp(-1,8837 + 0,0246*Возраст + 0,3010* Наличие заболеваний сердца)). Если в качестве клинического примера взять больного 26 лет, вероятность летального исхода составит 22,4%, а при наличии заболевания сердца 28,0%. У больного 74 лет вероятность летального исхода составит 48,4%, а при наличии заболевания сердца 55,9%. То есть факт наличия заболеваний сердца (ассоциированного предиктора для этого узла) увеличит риск летального исхода на 5,6% в 26 лет и на 7,5% в 74 года.
Далее в таблице 2 представлена характеристика терминальных узлов дерева решений (со второго по одиннадцатый узел).
Таблица 2
Характеристика терминальных узлов дерева решений
|
Узел 2 |
|||
|
Переменная |
Регрессионный коэффициент |
OR для коэффициента |
Уровень значимости p для коэффициента |
|
Свободный член |
-4,9648 |
– |
0,0146669 |
|
Возраст |
0,0666 |
1,0688 |
0,008157914 |
|
Уравнение зависимости: вероятность исхода = exp(-4,9648 + 0,0666*Возраст) /(1+exp(-4,9648 + 0,0666*Возраст)). Вероятность летального исхода будет увеличиваться в 1,06 раза с каждым годом жизни. При этом вероятность летального исхода между 75 и 80 годами на 8,2%, между 80 и 85 годами - на 6,7% и между 85 и 90 годами на 7%. |
|||
|
Узел 3 |
|||
|
Свободный член |
-12,1160 |
– |
0,000131 |
|
Возраст |
0,1718 |
1,18744 |
0,000013 |
|
СД |
1,2302 |
3,4219 |
0,014439 |
|
Уравнение зависимости: вероятность исхода = exp(-12,1160 + 0,1718*Возраст + 1,2302* Наличие сахарного диабета) / (1+ exp(-12,1160 + 0,1718*Возраст + 1,2302* Наличие сахарного диабета)). Вероятность летального исхода будет увеличиваться на 1,18 раза с каждым годом жизни. Ассоциированным предиктором летальности на этом узле будет являться наличие у больного СД, который в значительной степени будет увеличивать вероятность летального исхода (в 3,4 раза). При этом с увеличением возраста влияние СД как предиктора летального исхода будет уменьшаться. Разница прогнозов для больных 75 лет без СД и больных того же возраста с СД составит 19,8% (68,3% против 88,1% соответственно), 80 лет – на 11% (83,6% против 94,6%), в 85 лет - на 5,3% (92,3 %против 96,6 %); в 90 лет - на 2,4% (96,6% против 99%). |
|||
|
Узел 4 |
|||
|
Свободный член |
-5,3361 |
– |
<0,001 |
|
Возраст |
0,0319 |
1,0324 |
0,000018 |
|
Заболевания сердца |
0,6292 |
1,8760 |
0,000001 |
|
Уравнение зависимости: вероятность исхода = exp(-5,3361 + 0,0319*Возраст + 0,6292* Наличие заболеваний сердца) / (1+ exp(-5,3361 + 0,0319*Возраст + 0,6292* Наличие заболеваний сердца)). Вероятность летального исхода будет увеличиваться на 1,03 раза с каждым годом жизни и в 1,9 при наличии заболевания сердца. |
|||
|
Узел 5 |
|||
|
Свободный член |
-5,3130 |
– |
0,000006 |
|
Возраст |
0,0465 |
1,0476 |
0,007343 |
|
Уравнение зависимости: вероятность исхода = exp (-5,3130 + 0,0465*Возраст) / (1+ exp(-5,3130 + 0,0465*Возраст)). Вероятность летального исхода у больных будет зависеть от изменения возраста, увеличиваясь с каждым годом жизни на 1,05 раза и отличаться в среднем в 1,9 раза: в возрасте 44 лет вероятность летального исхода составит 3,7%, в 59 лет – 7,1%, в 74 года – 13,3%. |
|||
|
Узел 6 |
|||
|
Свободный член |
-5,6538 |
– |
0,000005 |
|
Возраст |
0,0611 |
1,0630 |
0,000857 |
|
Уравнение зависимости: вероятность исхода = exp(-5,6538 + 0,0611*Возраст) / (1+ exp(-5,6538 + 0,0611*Возраст)). Вероятность летального исхода у больных будет зависеть от изменения возраста, увеличиваясь с каждым годом жизни на 1,06 раза, и будет отличаться в среднем в 2,3 раза между возрастными группами: в возрасте 44 года вероятность летального прогноза составит 4,8%, в 59 лет – 11,4%, в 74 года – 24,4%. |
|||
|
Узел 7 |
|||
|
Свободный член |
-9,0873 |
– |
0,000002 |
|
Возраст |
0,0816 |
1,0850 |
0,000466 |
|
Заболевания сердца |
0,6186 |
1,8563 |
0,047482 |
|
Уравнение зависимости: вероятность исхода = exp(-9,0873 + 0,0816*Возраст + 0,6186* Наличие заболеваний сердца) / (1+ exp(-9,0873 + 0,0816*Возраст + 0,6186* Наличие заболеваний сердца)). Вероятность летального исхода инсульта имеет зависимость от возраста и наличия заболевания сердца: вероятность летального исхода будет увеличиваться в 1,09 раза с увеличением возраста на каждый год жизни и от наличия заболеваний сердца в 1,9 раза. Факт наличия заболеваний сердца увеличит риск летального исхода на 3,8% в 75 лет, на 5,4% в 80 лет и на 7,4% в 85 лет. |
|||
|
Узел 8 |
|||
|
Свободный член |
-10,6950 |
– |
<0,001 |
|
Возраст |
0,1085 |
1,1146 |
<0,001 |
|
Заболевания сердца |
0,6461 |
1,9080 |
0,002886 |
|
Уравнение зависимости: вероятность исхода = exp(-10,6950 + 0,1085*Возраст + 0,6461* Наличие заболеваний сердца) / (1+ exp(-10,6950 + 0,1085*Возраст + 0,6461* Наличие заболеваний сердца). В зависимости от возраста вероятность летального исхода у больных будет увеличиваться в 1,1 раза с каждым годом жизни. Наличие заболеваний сердца увеличивает вероятность летального исхода в 1,9 раза, на 5,7% в 75 лет, на 8,5% в 80 лет и на 11,7% в 85 лет. |
|||
|
Узел 9 |
|||
|
Свободный член |
-8,4797 |
– |
0,000093 |
|
Возраст |
0,0890 |
1,0931 |
0,000725 |
|
Уравнение зависимости: вероятность исхода = exp(-8,4797 + 0,0890*Возраст) / (1+ exp(-8,4797 + 0,0890*Возраст)). Вероятность летального исхода будет зависеть от изменения возраста, с увеличением неблагоприятного прогноза на 1,08 раза с каждым годом жизни. Между 75 и 80 годами будет отличаться на 2,8%, в возрасте 80 и 85 лет – на 3,5%. |
|||
|
Узел 10 |
|||
|
Свободный член |
-8,0137 |
– |
0,000802128 |
|
Возраст |
0,0763 |
1,0793 |
0,007984945 |
|
Заболевания сердца |
1,3121 |
3,7140 |
0,000409077 |
|
Уравнение зависимости: вероятность исхода = exp(-8,0137 + 0,0763*Возраст + 1,3121*Заболевания сердца) / (1+ exp(-8,0137 + 0,0763*Возраст + 1,3121*Заболевания сердца)). Увеличение возраста будет увеличивать риск вероятности летального исхода инсульта в 1,08 раза. Наличие заболеваний сердца будет увеличивать риск летального исхода в 3,7 раза. Между больными с отсутствием заболеваний сердца в возрасте 75 и 80 лет риск вероятности летального исхода инсульта будет отличаться на 3,7%, в возрасте 80 и 85 лет – на 4,9%. Факт наличия заболеваний сердца увеличит риск летального исхода на 18,1% в 75 лет, на 22,6% в 80 лет и на 26,8% в 85 лет. |
|||
|
Узел 11 |
|||
|
Свободный член |
-1,8090 |
– |
<0,001 |
|
Возраст |
0,0115 |
1,0116 |
0,018225 |
|
Заболевания сердца |
0,4759 |
1,6094 |
0,000156 |
|
Уравнение зависимости: вероятность исхода = exp(-1,8090 + 0,0115*Возраст + 0,4759* Наличие заболеваний сердца) / (1+ exp(-1,8090 + 0,0115*Возраст + 0,4759* Наличие заболеваний сердца)). Увеличение возраста будет увеличивать вероятность летального исхода в 1,01 раза на каждый год жизни. Заболевания сердца на момент развития инсульта увеличат вероятность летального исхода в 1,6 раза. Заболевания сердца будут увеличивать риск летального исхода на 5,6% в 26 лет и на 7,5% в 74 года. |
|||
Заключение. Предложенная прогностическая модель вероятности летального исхода инсульта на основе анализа статистически значимых предикторов летального исхода инсульта обладает высокой чувствительностью (73,84%) и специфичностью (70,50%) и может быть использована при разработке индивидуальных профилактических мер и клинических рекомендаций на всех этапах ведения больных инсультом, а также при разработке мер вторичной профилактики для снижения развития повторного инсульта.



