Главная цель школьной математики - научить решать задачи. И речь идет не только о задачах из учебников. Каждый день нас окружают различные задачи: где безопасно перейти улицу? Где купить еду и как ее приготовить? Это тоже задачи, которые каждый день нам задает жизнь, и которые школьник должен научиться решать. Конечно, многие задачи простые и повторяющиеся - они отрабатываются до автоматизма и перестают казаться чем-то сложным. Но жизнь так устроена, что появляются все новые и новые задачи. Поэтому так важно за время обучения в школе научиться решать задачи, в том числе и за пределами школы. Эта же цель была зафиксирована Государственным комитетом СССР по народному образованию в утвержденных им Программах по математике для средней школы за 1988, 1990 и 1991 годы.
Однако если посмотреть на результаты контрольных испытаний учащихся по математике, то видно, что как раз задачи школьники и решают хуже всего. Проблемы эти есть повсюду. Газета The New York Times начала дискуссию на тему, нужна ли детям алгебра, если каждый четвертый ученик в США не заканчивает школу из-за проблем с этим предметом [1]. А во Франции министр образования и науки, по образованию ученый-геофизик, всерьез обсуждал вопрос об отмене преподавания математики в школе, поскольку многие дети не справляются даже с элементарными задачами [2]. Эти факты показывают, насколько остро стоит проблема того, что школьники не могут решать задачи. А также доказывают, что проблему необходимо решать.
Цель исследования
Такая сложившаяся ситуация заставляет задуматься о причинах сложности задач. Во многих задачах до решения необходимо «догадаться». Но это могут делать далеко не все ученики. Тогда необходим общий подход, который без «догадок» позволял бы решать различные задачи. Отсюда целью данной работы является выявить или разработать наиболее понятный и эффективный метод решения задач, который могли бы использовать все школьники [3].
Материал и методы исследования
Начнем поиск наилучшего метода решения школьных математических задач среди традиционных существующих методов. С помощью содержательного анализа мы выявили среди множества найденных методов наиболее общеизвестные и часто применяемые. Данные методы рассмотрены в таблице 1. Для оценки предложенных методик необходимо выделить некоторые критерии эффективности применения методик. Автором были предложены следующие критерии: необходимые навыки (простота и доступность в применении), широта области применения, преимущества, недостатки. В таблице представлен сравнительный анализ предложенных методик по выбранным критериям.
Таблица 1
Сравнительные характеристики предложенных методик решения задач
|
Преимущества |
Недостатки |
|
Аналитико-синтетический метод |
|
|
Наиболее общий универсальный метод. |
Трудоемкий. Не предоставляет конкретного алгоритма решения задачи. |
|
Метод исчерпывающих проб |
|
|
Позволяет эффективно решать некоторые элементарные логические задачи. |
Трудоемкий. Узкая область применения - подходит для конкретных простых задач. Не предоставляет конкретного алгоритма решения задачи. |
|
Метод сведения к ранее решенным задачам |
|
|
Позволяет получить точный результат, если цепочка преобразований приводит к простому решаемому выражению. |
Узкая область применения. Не является исчерпывающим для большинства задач. Не предоставляет конкретного алгоритма решения задачи. |
|
Алгебраический метод (математическое моделирование) |
|
|
Адекватная качественная модель позволяет эффективно решить задачу. Решение уравнений/систем уравнений позволяет получить точный результат. |
Не предоставляет конкретного алгоритма построения математической модели задачи, что является главным в ее решении. |
|
Графический метод |
|
|
Позволяет эффективно решать определенную группу задач, является полезным для развития навыков всестороннего анализа задачи. |
Трудоемкий. Не является исчерпывающим для большинства задач: зачастую требует дополнительных методов, т.к. дает приближенный результат. Не предоставляет конкретного алгоритма решения задачи. |
|
Арифметический метод |
|
|
Получение точного числового значения в результате. |
Узкая область применения. Не предоставляет конкретного алгоритма решения задачи. |
|
Практический (предметный) способ |
|
|
Позволяет не выполнять арифметических действий. |
Узкая область применения - подходит только для элементарных задач на счет. |
Обобщая результаты анализа перечисленных способов решения математических задач, можно сказать, что эти способы слишком общие и, как правило, трудозатратные. Охватывая довольно узкий диапазон задач, они не предоставляют конкретного алгоритма решения этих самых задач. По сути, благополучный исход во многом приходится на долю случая и сообразительности решателя, а это, как известно, величины не постоянные. Таким образом, целесообразно разработать новый метод, который бы учитывал все недочеты существующих методик.
Результаты исследования и их обсуждение
В ходе исследования был разработан авторский метод решения задач – технология решения задач методом табличного анализа. Даная технология эффективно устраняет недостатки вышеизложенных традиционных методов - она дает в распоряжение универсальные алгоритмы, следование которым гарантирует успешное решение математических задач школьного уровня. Технология решения задач методом табличного анализа позволяет схематично решать любые задачи. Единственное ограничение на применение данного метода – для его применения необходимо хорошо знать явления и законы, о которых идет речь в задаче. Метод можно представить в виде 11 этапов.
Этап 1. Внимательно прочитать условия. При чтении условий необходимо убедиться, что каждое слово понятно. Перед решением задачи надо выяснить значение всех слов в тексте, так как каждое слово может существенно менять смысл задачи.
Этап 2. Определение закона. Далее необходимо понять, на каком законе основывается данная задача. Для того чтобы правильно определить закон, смотрим, какие характеристики участников нам даны в условиях задачи. Здесь участники – это объекты, которые в задаче обладают количественными характеристиками.
Этап 3. Составление таблицы
З.1. Определение характеристик. Метод табличного анализа основан на применении таблицы для решения задачи. Таблица позволяет наглядно отразить все условия задачи. В первом столбце таблицы перечисляем участников задачи. В остальных столбцах записываем характеристики данных участников, которые связаны между собой известным нам законом, описывающим явление в задаче. Закон (формулу) записываем в форме распределения одной величины по другой. В школьных задачах возможно до пяти. Бывают задачи с одной характеристикой. Характеристик может быть и больше, и закон может быть записан не только в форме распределения – технология не накладывает ограничений с этих сторон.
3.2. Определить единицы измерения характеристик. В таблицу необходимо вписать единицы измерения каждой характеристики. Это позволит сверить, в тех ли единицах измерения мы вносим в таблицу численные данные из условий задачи. Если в условиях задачи указаны данные в других единицах, то перед внесением в таблицу их необходимо перевести в те, которые мы указали в оглавлении столбцов характеристик.
3.3 Определение участников. Формально Участник может быть один, но если он выступает на разных участках, в разные интервалы времени и т.д., то будет несколько Участников, или один и тот же участник в разных Ситуациях. Бывают задачи с тремя Ситуациями и более. Если при внесении численных данных из условий задачи некоторые данные некуда записать, значит, мы пропустили Участника. Таким образом, таблица помогает отследить, всех ли Участников мы учли для решения задачи. Недостающего Участника тоже необходимо дописать в таблицу. В различных задачах требуется Участник «Вместе». Бывают такие Участники, как «Остаток» или «Прочее». Если сомневаемся в необходимости Участника, то лучше его написать, так как если не понадобится, то ячейки просто останутся пустыми.
3.4. Расставить действия. Для удобства решения, характеристики должны быть записаны в том порядке, в котором они расположены в законе (формуле), которым они связаны. Тогда возможно сразу показать взаимодействие характеристик в формуле. Для этого в шапке таблицы между характеристиками расставим математические действия (сложение, вычитание, умножение, деление).
Таблица составлена и готова для решения задачи.
Этап 4. Перенос численных данных из текста задачи в таблицу. Записываем в таблицу все численные данные из «Дано». Контролируем, чтобы данные были в тех единицах измерения, какие указаны в заголовках столбцов. Если данные относятся не к ячейке, а к связи между ними (равно, больше, меньше – «на» и «в»), то указываем стрелочку между связанными ячейками с указанием действия, по которому переходим из одной ячейки в другую. Связь также можно указать отдельным Участником «Увеличение» («Уменьшение») – особенно в задачах на %. Очень важно определить все связи между ячейками. Если в задаче несколько Ситуаций, то между ними обязательно должны быть связи, иначе задача не решится.
Этап 5. Обозначить искомые величины. Ставим знак «?» в те ячейки, в которых находятся искомые данные.
Этап 6. Проверка. Внимательно перечитываем задачу и проверяем, все ли данные и связи указаны в таблице. Если задача не решается, то значит, что мы не увидели каких-то связей либо скрытых данных.
Этап 7. Выполняем действия с известными данными в таблице. Делаем действия, которые уже можно сделать в таблице. Есть задачи, которые решаются прямо в таблице – без введения дополнительных неизвестных.
Этап 8. Вводим Неизвестное. Если задача не решилась после выполнения всех действий с известными данными в таблице, то вводим «Неизвестное». Неизвестное надо вводить так, чтобы: во-первых, заполнилось максимальное количество ячеек по связям, во-вторых, с неизвестной было действие умножения или сложения (умножать проще, чем делить, а вычитать сложнее, чем складывать). Приоритет отдаем первому условию, так как бывает, что без деления и вычитания не обойтись.
Этап 9. Выполняем действия с неизвестными. Делаем все возможные действия с неизвестным, чтобы заполнить как можно больше ячеек таблицы. Если с введенной Неизвестной по связям в таблице получилось уравнение – выписываем его отдельно под таблицей. Уравнение из таблицы получается в математическом виде - без единиц измерения. Единицы измерения «удерживает» сама таблица.
Этап 10. Вводим вторую Неизвестную. Если после выполнения всех действий с одной неизвестной задача не решается (есть еще искомые величины, которые не охватываются одной неизвестной), то вводим Вторую Неизвестную по тем же принципам, как и Первую (см. этап 8). Заполняем ячейки таблицы со Второй Неизвестной. Выписываем два уравнения с двумя неизвестными. Получаем систему уравнений.
Этап 11. Выписываем уравнения из таблицы. После выполнения этапов 9 или 10 мы должны получить Уравнение или Систему Уравнений. Если мы затрудняемся их выписать из таблицы, значит, либо не отметили какой-то связи, либо запутались в связях – потеряли, какие связи уже использовали, а какие – нет. Тогда можно каким-либо образом, например «птичками» на связях, отметить прямо в таблице, по каким связям уже прошли вычисления, - оставшиеся неотмеченными связи и надо использовать для составления уравнений.
На этом применение метода табличного анализа закончено – остается решить Уравнение или Систему Уравнений и получить ответ. Далее разберем пример решения задачи с использованием технологии решения задач методом табличного анализа.
Задача: На речном трамвайчике можно совершить трехчасовую прогулку до поворота реки и обратно. Скорость течения реки 2 км/ч. Собственная скорость трамвайчика 15 км/ч. Какова длина прогулочного маршрута?
Решение: Этап 1. Внимательно прочитать условия. Читаем условие.
Этап 2. Определение закона. Данная задача на закон равномерного движения по реке (по течению и против течения). Формула: V =L/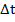 . Далее составляем таблицу.
. Далее составляем таблицу.
З.1. Данная задача содержит три характеристики: путь, время и скорость, связанные законом равномерного движения: V =L/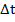 . Поэтому делаем табличку из четырех колонок.
. Поэтому делаем табличку из четырех колонок.
3.2. Единицы измерения характеристик: Путь (L) – в км; Время (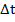 ) – в часах (ч); Скорость (V) – в км/ч. Записываем данные единицы рядом с характеристиками в шапке таблицы.
) – в часах (ч); Скорость (V) – в км/ч. Записываем данные единицы рядом с характеристиками в шапке таблицы.
3.3 Определение участников. В рассматриваемой задаче три участника: «трамвайчик», «река» и «вместе» (так как трамвайчик движется по реке). И эти участники встречаются в двух ситуациях – движение по течению и против течения.
3.4. Расставляем математические действия между характеристиками: «деление» между Длиной и Временем, знак «равно» между Временем и Скоростью (табл. 2).
Этап 4. Перенос численных данных из текста задачи в таблицу. Заполняем таблицу численными данными (табл. 2, данные черным шрифтом). Учитываем, что скорость течения реки и трамвайчика одинаковы в обеих ситуациях.
Этап 5. Обозначить искомые величины. В задаче надо найти длину всего прогулочного маршрута (туда и обратно), а в таблице сейчас нет такой ячейки. Кроме того, нам некуда поставить общее время движения – туда и обратно. Таким образом, таблица «подсказывает», что надо ввести еще одного участника «Итого». Дополняем участника «Итого» и обозначаем путь «Итого» знаком «?».
Этап 6. Проверка. Проверили, все ли данные занесены в таблицу из условий задачи. Отметим, что пути «Вместе» туда и обратно равны между собой, а также укажем стандартные связи для движения по течению (скорости складываются) и против течения (скорости вычитаются).
Этап 7. Выполняем действия. Выполним сложение и вычитание скоростей.
Этап 8. Введем неизвестное в ячейку времени движения по течению – х час.
Этап 9. Выполняем действия с неизвестными. После ввода неизвестной можем заполнить ячейки «Путь» по течению, «Время» и «Путь» против течения. Этап 10 опускаем.
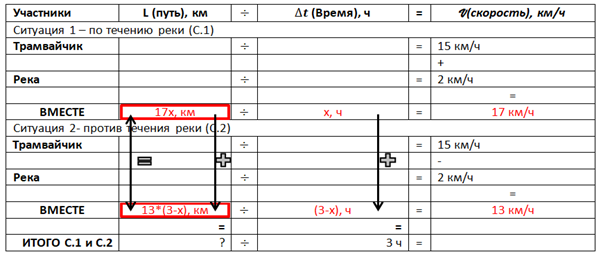
Этап 11. Выписываем уравнения из таблицы. После этапа 9 по связи в колонке «Путь» получилось уравнение (табл. 2, красные рамки). Выпишем его: 17х=13*(3-х). Теперь решаем уравнение и получаем: х = 1,3. Находим ячейку «Путь» по течению: 17х=17*1,3=22,1. Находим ячейку «Путь» в строчке «Итого»: 22,1+22,1=44,2. Ответ: 44,2 км.
Решение закончено. В таблице 2 показан заполненный шаблон с решением задачи методом табличного анализа.
Таблица 2
Шаблон таблицы с решением задачи методом табличного анализа
Заключение
В данной задаче (как и в других) можно, конечно, догадаться и до другого решения. Разница в представленном подходе заключается в том, что при следовании технологии решения задач ученику не надо «догадываться». Надо отработать применение технологии на практике, и результат гарантирован. При этом метод табличного анализа, как правило, приводит к результату проще, чем методом физического анализа.
Таким образом, в данной работе предложена авторская технология решения задач методом табличного анализа. Возможности ее использования показаны на примере решения текстовой задачи по математике (одновременно и по физике) на движение по реке уровня школьной программы. Преимущество данной методики заключается в наглядности и схематичности решения. В то же время соблюдается детальность и поэтапность решения. Также необходимо отметить наличие алгоритма действий, что позволяет на основании данной методики решать задачи по математике и физике множества типов и тематик. Разработанная методика рассчитана на школьников любого возраста [4; 5] и применима к решению любых текстовых задач.



