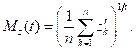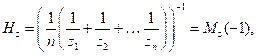При исследовании различных технических проблем экономических и социальных явлений невозможно обойтись без использования математических методов создания моделей. Моделирование позволяет создать надежную основу для управления различными процессами с помощью компьютерных технологий.
При изучении экономических и технических предметов в высшей школе в той или иной мере применяются знания, полученные при изучении элементарной и высшей математики. В частности, при создании динамических моделей социальных и экономических задач зачастую приходится находить аналитическую связь между переменными по заданным статистическим данным, другими словами – аппроксимировать некоторую функцию, для которой известны лишь отдельные значения при определенных значениях аргумента.
Решение указанной задачи состоит из двух важных этапов. Сначала устанавливается вид эмпирической формулы из некоторого заранее определенного класса функций, а затем с помощью известных методов математической статистики находятся ее параметры. Удачно подобранный вид формулы зависимости между исследуемыми признаками является залогом создания модели, адекватной исследуемому явлению. При этом анализ механизма изучаемой зависимости, основанный на познании сущности ее природы, является главным основанием для выбора вида модели. Поскольку реальные социально-экономические процессы не отличаются простотой, а экзогенные переменные, от которых они зависят, зачастую взаимосвязаны, то на теоретическом уровне вид зависимости эндогенной переменной от отдельных факторов не всегда представляется возможным установить.
Цель исследования. В методическом обеспечении преподавания разделов эконометрики одной из недостаточно разработанных проблем подачи материала является вопрос о способах выбора эмпирической формулы. В большинстве источников с этой целью зачастую предлагаются ничем не обоснованные наборы функций, которые, по мнению их составителей, наиболее востребованы в практике обработки результатов наблюдений. Целью настоящего исследования является разработка методически обоснованного подхода к выбору вида уравнения регрессии из определенного класса монотонных гладких функций. В качестве теоретической основы в данной работе использованы принципы выбора общего вида функции регрессии, предложенные С.А. Айвазяном [1, с. 66]:
Качественное проведенное выявление класса функции, которые будут образовывать множество допустимых решений задачи, среди которых будет осуществляться поиск регрессионных зависимостей, закладывает предпосылки к дальнейшему получению качественной модели процесса. Однако эта часть регрессионного анализа недостаточно теоретически разработана и обоснована. При определении эмпирической формулы, используемой в качестве функции регрессии, в первую очередь необходимо изучить глубинную сущность моделируемой зависимости с целью использования известных априорных данных о механизме функционирования исследуемого явления. Неоценимую помощь в этом может оказать геометрический анализ имеющихся статистических данных. Для этого надо рассечь многомерную гиперповерхность, которую предполагается построить по заданному набору статистических данных, гиперплоскостями уровня. При этом будут получаться парные корреляционные поля, по виду которых можно делать выводы о монотонности и порядке «гладкости» частных функций отклика, наличии асимптот, возможности линеаризации функций с помощью замены переменных и некоторых других их свойствах.
Для проверки гипотез о виде предполагаемой эмпирической формулы, полученной с помощью содержательного и геометрического анализа процесса, можно использовать методы, разработанные в математической статистике для проверки гипотез.
Материал и методы исследования. К сожалению, в учебной литературе по эконометрике зачастую присутствует формальный подход. Сначала предлагается научить студентов построению моделей, а лишь затем провести проверку полученных результатов на соответствие имеющейся априорной информации об исследуемом в процессе. В частности, в ряде учебных пособий при построении нелинейной парной регрессии по заданному набору экспериментальных точек предлагается не задумываясь применять встроенную в МS Excel функцию построения линии тренда, хотя заведомо известно, что по экономическим соображениям некоторые из них применять не следует.
При такой методической реализации преподавания регрессионного анализа у студентов зачастую складывается мнение о том, что лучшую модель, аппроксимирующую заданный набор точек, можно найти, если использовать многочлен высокой степени. Но если экономический или физический смысл решаемой задачи предполагает монотонность процесса, то очевидно, это приведет к получению неверных результатов, хотя по критерию минимизации погрешностей полиномиальная модель дает лучший результат. Так, например, не имеет смысла на большом интервале изменения переменных использовать квадратичную функцию (параболу) для моделирования функции спроса на изделие от его цены, поскольку эта зависимость строго монотонная и к тому же теоретически обладает асимптотой.
Сущностный анализ рассматриваемого явления должен являться основой при выборе виды эмпирической формулы, используемой при построении модели [2, 3]. Для этого надо учитывать не только основные теоретические соображения о характере процесса и свойствах его факторов, но и воздействие других экономических, технологических и социальных процессов, которые могут повлиять на функционирование моделируемого процесса.
При восстановлении эконометрических зависимостей часто приходится учитывать не только то, что они должны быть монотонными и достаточно «гладкими», но и некоторые другие их качественные характеристики. В частности, экономические соображения могут диктовать необходимость того, чтобы график искомой функции не имел точек перегиба. В настоящей работе представлен подход, с помощью которого можно определять наиболее подходящий вид эмпирический формулы для установления регрессионной зависимости между двумя переменными, учитывающей указанную особенность [4, 5].
Свойство обобщенного среднего для монотонных двупараметрических функций
Будем использовать в качестве эмпирических формул функции вида ![]() , зависящие от двух параметров:
, зависящие от двух параметров:
|
|
если |
|
(1) |
|
|
если |
|
(2) |
|
|
если |
|
(3) |
|
|
|
|
(4) |
Эти функции (1–4) обладают общим свойством, связанным с так называемым обобщенным средним положительных чисел ![]()
|
|
(5) |
Средние гармоническое ![]() (6), геометрическое
(6), геометрическое ![]() (7), арифметическое
(7), арифметическое ![]() (8) и квадратическое
(8) и квадратическое ![]() (9) представляют собой частные случаи обобщенного среднего (5):
(9) представляют собой частные случаи обобщенного среднего (5):
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
При этом ![]()
Авторами выявлено общее свойство функций (1–4):
|
|
(10) |
К примеру, если ![]() и
и ![]() взять равными нулю, то получим функцию
взять равными нулю, то получим функцию ![]() , для которой имеет место равенство
, для которой имеет место равенство ![]() или по-другому
или по-другому ![]() .
.
Беря ![]() и
и ![]() , равные –1; 0; 1; 2, получим 16 монотонных функций, среди которых, в частности, есть: линейная, квадратичная, гиперболическая, показательная, логарифмическая, степенная и другие функции, с которыми студентам приходится иметь дело при изучении эконометрики. Пусть на координатную плоскость (рис. 1) нанесены результаты измерений
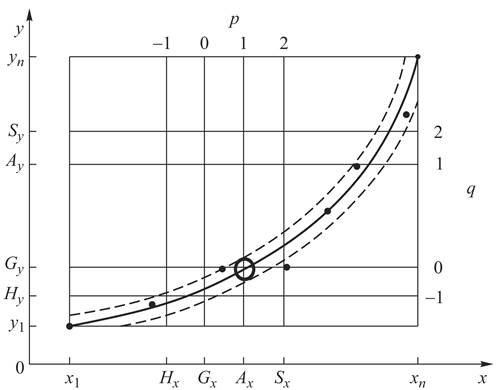
, равные –1; 0; 1; 2, получим 16 монотонных функций, среди которых, в частности, есть: линейная, квадратичная, гиперболическая, показательная, логарифмическая, степенная и другие функции, с которыми студентам приходится иметь дело при изучении эконометрики. Пусть на координатную плоскость (рис. 1) нанесены результаты измерений ![]()
![]() Под графиком искомой функциональной зависимости понимается кривая, проходящая через середину полосы разброса экспериментальных данных (рис. 1). Предполагается, что построенная кривая отображает тенденцию, присущую ряду данных, и при этом является свободной от незначительных колебаний, обусловленных погрешностями измерений. Возьмем две крайние точки
Под графиком искомой функциональной зависимости понимается кривая, проходящая через середину полосы разброса экспериментальных данных (рис. 1). Предполагается, что построенная кривая отображает тенденцию, присущую ряду данных, и при этом является свободной от незначительных колебаний, обусловленных погрешностями измерений. Возьмем две крайние точки ![]() и
и ![]() кривой, полагая их достаточно надежными. Вычислим средние гармоническое
кривой, полагая их достаточно надежными. Вычислим средние гармоническое ![]() , геометрическое
, геометрическое ![]() , арифметическое
, арифметическое ![]() , квадратическое
, квадратическое ![]() . Подсчитаем средние
. Подсчитаем средние ![]() .
.
Исследование моделируемой зависимости
Найденные значения отметим на соответствующих координатных осях и проведем через них прямые, которые пересекутся в шестнадцати точках, соответствующих формулам таблицы.
Двупараметрические эмпирические функции, соответствующие им средние и линеаризующие преобразования
|
№ п/п |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
2 |
|
1 |
0 |
|
|
|
|
|
|
|
3 |
|
1 |
–1 |
|
|
|
|
|
|
|
4 |
|
0 |
1 |
|
|
|
|
|
|
|
5 |
|
–1 |
1 |
|
|
|
|
|
|
|
6 |
|
0 |
0 |
|
|
|
|
|
|
|
7 |
|
–1 |
–1 |
|
|
|
|
|
|
|
8 |
|
–1 |
0 |
|
|
|
|
|
|
|
9 |
|
0 |
–1 |
|
|
|
|
|
|
|
10 |
|
2 |
1 |
|
|
|
|
|
|
|
11 |
|
2 |
0 |
|
|
|
|
|
|
|
12 |
|
2 |
–1 |
|
|
|
|
|
|
|
13 |
|
2 |
2 |
|
|
|
|
|
|
|
14 |
|
1 |
2 |
|
|
|
|
|
|
|
15 |
|
0 |
2 |
|
|
|
|
|
|
|
16 |
|
–1 |
2 |
|
|
|
|
|
|
В качестве эмпирической формулы искомой аналитической зависимости следует выбирать ту, которая соответствует ближайшей к графику точке пересечения прямых. Так, на рисунке 1 кривая проходит через точку пересечения прямых, соответствующую показательной функции ![]() (№ 2 в табл. 1).
(№ 2 в табл. 1).
Если таких точек пересечения прямых оказалось несколько, то надо дополнительно проверить, насколько удовлетворяют соответствующие им формулы априорным сведениям, а также теоретическим предпосылкам об искомой зависимости. Легко доказывается, что все представленные функции являются линеаризуемыми, поэтому для них методом наименьших квадратов можно найти значения параметров ![]() ,
, ![]() и общую погрешность измерений. Тогда в качестве лучшей следует выбирать функцию, отвечающую минимальной сумме мер отклонений.
и общую погрешность измерений. Тогда в качестве лучшей следует выбирать функцию, отвечающую минимальной сумме мер отклонений.
Аппроксимирующие аналитические выражения должны как можно более точно описывать реальные показатели. Однако повышение точности аппроксимации приводит, как правило, к усложнению аппроксимирующих функций, что затрудняет как определение значений входящих в эти формулы параметров, так и использование этих выражений для анализа явлений. Если вычисления по построенной модели значительно отличаются от имеющихся данных, то применяемые двупараметрические эмпирические формулы можно дополнить еще одним параметром. Его можно включить в формулу, используя дополнительные дифференциально-геометрические условия, предъявляемые к восстанавливаемой зависимости. В частности, в качестве третьего параметра можно использовать ![]() или
или ![]() .
.
Представленный набор двупараметрических формул может быть неограниченно увеличен путем придания ![]() и
и ![]() любых числовых значений. Решение вопроса о том, при каких
любых числовых значений. Решение вопроса о том, при каких ![]() и
и ![]() эмпирическая зависимость наилучшим образом будет аппроксимировать имеющиеся экспериментальные данные, зависит от спецификации исследуемой модели. Если же
эмпирическая зависимость наилучшим образом будет аппроксимировать имеющиеся экспериментальные данные, зависит от спецификации исследуемой модели. Если же ![]() или
или ![]() известно, то другой параметр можно определить приближенно графически или более точно, решая неявное уравнение.
известно, то другой параметр можно определить приближенно графически или более точно, решая неявное уравнение.
Результаты исследования и их обсуждение
Для успешного освоения эконометрики обучающиеся должны иметь запас знаний по основным понятиям и методам математической статистики: цели и методы сбора статистических данных, первичная обработка статистических данных, основные характеристики случайных величин, основные статистические распределения, таблицы распределений и их использование, получение доверительных интервалов, проверка статистических гипотез. Все темы должны быть закреплены решением практических задач, желательно на реальных статистических данных.
Вместе с разработкой соответствующего методического обеспечения [6–8] необходимо решать проблему внедрения информационных технологий в процесс обучения эконометрике, поскольку решение научно-практических задач обусловлено многочисленными расчетами, статистической обработкой и анализом данных. Поэтому овладение методологическими понятиями эконометрики на качественно новом уровне возможно только с применением информационных технологий [9–11].
Современные компьютерные программы обработки данных позволяют строить уравнения регрессий для отдельных функций рассмотренного класса и выбирать из них ту, для которой остаточная дисперсия и ошибка аппроксимации минимальны, а коэффициент детерминации максимален. Однако для получения обоснованно лучшего результата исследователю следует добавить отсутствующие двупараметрические формулы из указанного выше перечня в предлагаемый программой имеющийся комплект регрессионных моделей.
При этом важно донести до студентов тот факт, что каждая модель есть конгломерат объективной информации, субъективных сведений, практикуемых подходов, а также математических действий. В конце концов, любая математическая модель конкретного экономического объекта, даже построенная на базе общепризнанных положений экономической теории, содержит существенную долю субъективных решений. Поэтому и рекомендации, основанные на расчетах с использованием таких моделей, не могут быть вполне объективными.
Следует отметить, что в эконометрической литературе, а также в известных пакетах прикладных программ до сих пор отсутствует логически обоснованный набор эмпирических формул. Так, в справочнике [12] представлены 7 из 16 рассмотренных функций с алгоритмом выбора лучшей из них для аппроксимации данных. Но при этом не объясняется, каким образом был определен этот набор. Предложенная методика дает ответ на поставленный вопрос и позволяет более системно подходить к вопросам изучения разделов эконометрики и математического моделирования, связанных с использованием нелинейных моделей парной регрессии.
Заключение
Одной из основных задач регрессионного анализа является нахождение вида аналитической зависимости между переменными, когда известны отдельные значения эндогенной переменной при заданных значениях экзогенных признаков. Во многих методических пособиях по эконометрике для нахождения лучшего уравнения парной регрессии предлагается с учетом возросших возможностей компьютерной техники использовать некоторый набор аппроксимирующих функций, выбирая из них ту, для которой отклонение от имеющихся данных будет минимальным. Такой подход не всегда является оптимальным по причине того, что выбранная функция может и не удовлетворять экономическим или дифференциально-геометрическим требованиям к модели процесса (или просто отсутствовать в используемом в наборе).
В работе представлен методический подход, позволяющий выбрать лучшую аппроксимирующую функцию из класса монотонных двупараметрических функций, значение каждой из которых в точке, соответствующей обобщенному среднему по аргументу х, равно обобщенному среднему по переменной у. В отличие от других наборов эмпирических формул, традиционно предлагаемых в литературе по экономико-математическому моделированию для обработки результатов наблюдений, представленные функции объединены общим свойством, характеризующим логику их объединения для решения поставленной задачи. К тому же эта логика позволяет при необходимости неограниченно расширить предлагаемый перечень формул и показывает направление исследований по их модификации с целью внедрения третьего параметра. При этом учитывается не только статистическая, но и аналитическая информация об исследуемом явлении.
Реализация предложенной методики была успешно осуществлена авторами при подготовке магистров по дисциплинам «Математическое моделирование» в МГТУ им. Н.Э. Баумана и «Эконометрика (продвинутый уровень)» в РЭУ им. Г.В. Плеханова. С уверенностью можно заявить о необходимости внедрения представленной методики в учебный процесс и обновления соответствующих разделов многочисленных учебных пособий, в которых представлены материалы о выборе вида уравнения регрессии из класса гладких монотонных функций.