Динамическое развитие химических технологий предполагает повышение требований к подготовке будущих инженеров. Понимание этих требований и их реализация позволяют обеспечить качественную подготовку инженеров по всем учебным дисциплинам, в том числе и по математике.
Математический аппарат предусматривает раскрытие особенностей нелинейных природных явлений. В связи с этим приоритетными в обучении математике становятся методы математического анализа, направленные на описание и выявление сущности изучаемых процессов.
Одной из важнейших задач подготовки будущих инженеров является владение анализом и оценкой химико-технологического процесса, знание основных его особенностей и закономерностей.
Эти идеи зафиксированы в Федеральном государственном образовательном стандарте высшего образования по направлению 18.03.02 «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии» [1], где подчеркивается, что анализ и оценка технологической системы и отдельных ее узлов является одной из профессиональных задач, которые должен решать выпускник в результате освоения образовательной программы.
Инженерное образование предполагает и междисциплинарную интеграцию, позволяющую связать воедино различные области знаний, в частности общую химию, общую физику и классическую математику, в одну систему, которая является логической основой становления будущего инженера.
Осуществление подготовки будущих инженеров-технологов к анализу и оценке процессов химической технологии обеспечивается интеграцией следующих дисциплин: «Математика», «Процессы и аппараты химической технологии» и «Моделирование химико-технологических процессов» (рис. 1).
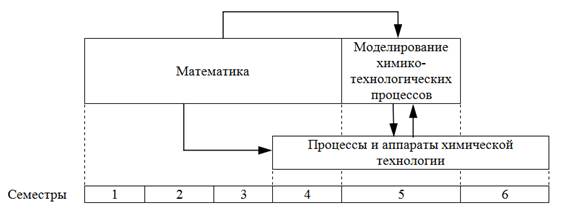
Рис. 1. Междисциплинарная интеграция
При изучении курса «Процессы и аппараты химической технологии» студенты овладевают основными закономерностями химико-технологических процессов (виды, особенности протекания, возможный результат) и проводят их анализ на основе фундаментальных законов физики, химии, физической химии, термодинамики и других наук. Освоение спецдисциплины «Моделирование химико-технологических процессов» способствует обучению студентов решению профессиональных задач, направленных на моделирование процессов химической технологии с учетом выбора определяющих факторов и оптимальных условий протекания процесса.
Следует заметить, что химико-технологический процесс достаточно сложный и представляет собой совокупность более простых физических, химических и физико-химических процессов.
По мнению А.Г. Касаткина, химико-технологические процессы следует классифицировать, основываясь на законах, которые определяют скорость протекания процессов [2]:
- гидромеханические процессы, скорость которых определяется законами гидродинамики;
- тепловые процессы, которые протекают со скоростью, определяемой законами теплопередачи;
- массообменные процессы, характеризующиеся переносом одного или нескольких компонентов исходной смеси из одной фазы в другую через поверхность раздела фаз;
- химические (реакционные) процессы, которые протекают со скоростью, определяемой законами химической кинетики.
Следовательно, при изучении химико-технологического процесса целесообразно: во-первых, рассмотреть особенности протекания отдельных процессов, входящих в его структуру; во-вторых, для каждого процесса научиться выбирать оптимальный режим; в-третьих, для управления процессом в условиях многофакторности его протекания необходимо уметь анализировать процесс, выделять значимые факторы и оценивать их воздействие на результат.
В.В. Кафаров [3] подчеркивает, что «внешний потенциал информации о химико-технологических процессах очень велик», поэтому изучение процесса возможно с помощью построения его модели.
Овладение методами моделирования химико-технологических процессов - от составления математической модели процесса, которая отражает его основные особенности и может быть решена либо аналитически, либо численно за разумное время, до составления алгоритма решения, выбора вычислительных средств, средств визуализации и анализа результатов моделирования - является основным требованием в подготовке «современного инженера» [4].
Существует множество различных подходов к определению понятия «моделирование» (В.Ф. Беккер [5], Е.Н. Коржов [6] и др.).
Вслед за Е.Н. Коржовым [6], под моделированием будем понимать исследование основных закономерностей и особенностей функционирования реальных объектов с помощью моделей в целях возможности предсказания их поведения в определенных условиях.
Различают физическое и математическое моделирование химико-технологических процессов.
Физическое моделирование предполагает построение новой модели для каждого изучаемого явления, что достаточно трудоемко и затруднительно. Для сложных процессов и систем создание такой модели бывает практически невозможным.
Трудности физического моделирования, согласно В.Ф. Беккеру [5], удается преодолеть с помощью математического моделирования. В связи с этим основным методом расчета сложных процессов химической технологии становится метод математического моделирования [3].
Обосновывая значимость математического моделирования для студентов инженерных специальностей, Т.И. Алиев [7] подчеркивает, что результаты математического моделирования позволяют определить значения показателей эффективности системы, обосновать её оптимальную структуру и составить рекомендации по совершенствованию исследуемых вариантов.
Применительно к химической технологии математическая модель представляет собой совокупность математических зависимостей, отражающих сущность химико-технологического процесса и связывающих его физические, режимные, физико-химические и конструктивные параметры [8]. При этом адекватное отображение моделируемых свойств химических веществ представлено в математической форме [9].
На основании вышесказанного можно сделать вывод, что подготовка студента к анализу и оценке химико-технологического процесса зависит от его умения проводить анализ и оценку математических моделей различных процессов химической технологии.
Инженерный анализ, в общем случае, представляет собой исследование, основанное на построении упрощенных моделей, учитывающих лишь основные аспекты поведения [10].
В связи с этим необходима оценка, которую следует рассматривать как категорию цели, позволяющей определять значение того или иного материала для решения конкретной профессиональной задачи [11], а применительно к математической модели химико-технологических процессов - как выбор факторов, оказывающих существенное влияние на протекание процесса.
На основе проведенного анализа описания этапов математического моделирования разными авторами (А.Н. Боголюбов [12], В.Ф. Беккер [5], Ю.Б. Мельников [13] и др.) можно выделить следующие этапы.
1. Математическое обоснование модели, которое включает в себя:
- определение цели моделирования;
- анализ содержания изучаемого материала;
- выделение существенных свойств и закономерностей, необходимых для исследования.
2. Математическое описание модели − перевод на математический язык закономерностей и зависимостей, выделенных на первом этапе.
3. Анализ и выбор возможных методов решения (аналитический, геометрический, численный) и их реализация.
4. Проверка и оценка адекватности модели.
5. Интерпретация полученных результатов.
6. Рассмотрение возможностей использования полученной модели.
Рассмотрим возможность подготовки к анализу и оценке математической модели теплового процесса в процессе обучения математике.
В первом семестре при изучении раздела «Дифференциальное исчисление функции одной переменной», как и сказано в работе Л.И. Львовой [14], целесообразно перечислить наиболее часто применимые механические, физические и другие прикладные значения производной и пояснить форму их записи. Например:
 скорость изменения температуры
скорость изменения температуры 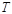 тела за единицу времени
тела за единицу времени 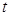 ;
;
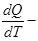 скорость изменения теплоты
скорость изменения теплоты 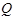 (теплоемкость тела) при изменении температуры
(теплоемкость тела) при изменении температуры 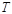 .
.
Во втором семестре, при изучении обыкновенных дифференциальных уравнений, следует рассмотреть задачи о переносе тепла, приводящие к дифференциальным уравнениям.
Для того чтобы студент смог провести анализ и оценку условия, перед задачей нужно пояснить студентам, что
- теплообмен − это процесс переноса тепла, происходящий между телами, имеющими различную температуру;
- разность температур является движущей силой данного процесса теплообмена, и в соответствии со вторым законом термодинамики тепло самопроизвольно будет переходить от более нагретого тела к менее нагретому.
Пример задачи. Тело, имеющее в начальный момент температуру 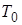 , поместили в среду, температура которой поддерживается неизменной и равна
, поместили в среду, температура которой поддерживается неизменной и равна 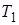 . Как будет изменяться с течением времени температура тела, если скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды?
. Как будет изменяться с течением времени температура тела, если скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды?
Решение. 1 этап (математическое обоснование модели).
Студент определяет цель моделирования − составление уравнения, которое будет описывать изменение температуры тела при заданных условиях и являться моделью данного процесса передачи тепла.
На основе анализа условия задачи и оценки факторов, влияющих на процесс, студент выделяет основные зависимости и закономерности:
- значение температуры зависит от времени, то есть является функцией;
- скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды, таким образом, необходимо учесть коэффициент пропорциональности.
2 этап (математическое описание модели).
Студент переводит выделенные зависимости и закономерности на математический язык: 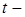 значение времени,
значение времени,  значение температуры в момент времени
значение температуры в момент времени 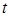 ;
; 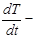 скорость изменения температуры за единицу времени;
скорость изменения температуры за единицу времени; 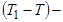 разность температур тела и среды;
разность температур тела и среды; 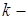 коэффициент пропорциональности.
коэффициент пропорциональности.
При составлении дифференциального уравнения, анализируя условие, что скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды, студент определяет, что для уравнивания величин необходимо умножить на коэффициент пропорциональности (оценка значения коэффициента пропорциональности):
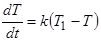 .
.
3 этап (анализ и выбор возможных методов решений). Проводя анализ вида уравнения, студент отмечает, что переменные можно разделить, то есть полученное уравнение является дифференциальным уравнением с разделяющимися переменными:
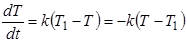 ;
; 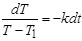 ;
;
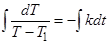 ;
; 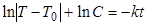 ;
;
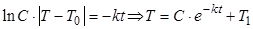 .
.
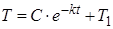 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Для нахождения параметра 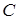 студент проводит анализ и оценку условий, позволяющих найти частное решение дифференциального уравнения, а именно, что в начальный момент времени
студент проводит анализ и оценку условий, позволяющих найти частное решение дифференциального уравнения, а именно, что в начальный момент времени 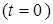 температура тела равна
температура тела равна 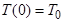 , тогда
, тогда
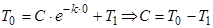 .
.
И частное решение дифференциального уравнения имеет вид: 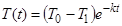
4 и 5 этапы (проверка и оценка модели, интерпретация результатов).
В результате студент делает вывод, что полученная функция 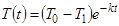 описывает изменение температуры тела с течением времени. Для интерпретации данной математической модели запишем функцию в виде:
описывает изменение температуры тела с течением времени. Для интерпретации данной математической модели запишем функцию в виде: 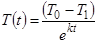 .
.
Проводя анализ и оценку данной модели, студент отмечает, что функция выражает обратную зависимость температуры от времени, то есть при увеличении времени температура тела будет снижаться.
6 этап (рассмотрение возможностей использования полученной модели).
В качестве примера использования модели можно рассмотреть задачу с конкретными числовыми значениями температуры и времени, а также построить графическое изображение полученной функциональной зависимости.
В третьем семестре при изучении темы «Функция нескольких переменных» в качестве примера следует рассмотреть температурное поле, которое как математический объект представляет собой функцию нескольких переменных 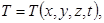 то есть каждой точке некоторого тела в каждый момент времени ставится в соответствие числовое значение температуры.
то есть каждой точке некоторого тела в каждый момент времени ставится в соответствие числовое значение температуры.
Если существенным является изменение только вдоль одной координаты, то температурное поле называется одномерным, если вдоль двух координат, то соответственно двумерным. Например, на рисунке изображено тело, имеющее начальную температуру (рис. 2).

Рис. 2. Изображение изменения температуры тела
Тело постепенно начинают нагревать или охлаждать путем подведения к левому концу источника тепла или холода. Температура данного тела в каждой точке будет зависеть от времени, прошедшего с начала процесса охлаждения или нагревания, и от расстояния данной точки. Таким образом, температура тела является функцией двух переменных 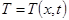 .
.
Далее при изучении раздела «Дифференциальное исчисление функции нескольких переменных» возможно провести анализ закона Фурье передачи тепла теплопроводностью для одномерного случая. Для этого следует сказать студенту о том, что частные производные 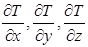 характеризуют изменения вдоль координатных осей скорость температуры тела в фиксированный момент времени. А градиент температуры - это есть вектор, направленный в сторону максимального возрастания температуры в пространстве и численно равный производной от температуры по этому направлению.
характеризуют изменения вдоль координатных осей скорость температуры тела в фиксированный момент времени. А градиент температуры - это есть вектор, направленный в сторону максимального возрастания температуры в пространстве и численно равный производной от температуры по этому направлению.
Также следует пояснить студенту, что, согласно закону Фурье о передаче тепла теплопроводностью, плотность теплового потока пропорциональна градиенту температуры:
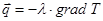 ,
,
где l − это коэффициент теплопроводности (характеризует способность тела проводить тепло путем теплопроводности, зависит от природы вещества, его структуры, температуры и других факторов).
Проводя анализ данной формулы для одномерного случая, студент делает вывод о том, что изменение температуры рассматривается только вдоль одной оси. В качестве рассматриваемой выбирает ось Ох, следовательно, 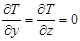 (оценка существенных факторов) и
(оценка существенных факторов) и 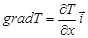 , а скалярная величина теплового потока будет равна
, а скалярная величина теплового потока будет равна 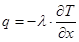 .
.
Анализируя полученную векторную формулу, студент отмечает, что знак минус в записи формулы означает, что вектор направления возрастания температуры 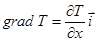 и вектор плотности теплового потока
и вектор плотности теплового потока 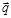 противоположно направлены. Проводя оценку данного фактора на математическом языке, студент делает вывод, о том, что если тепловой поток направлен в сторону увеличения переменной х, то
противоположно направлены. Проводя оценку данного фактора на математическом языке, студент делает вывод, о том, что если тепловой поток направлен в сторону увеличения переменной х, то 
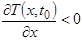 , а если же тепловой поток направлен в сторону уменьшения переменной х, тогда
, а если же тепловой поток направлен в сторону уменьшения переменной х, тогда 
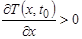 .
.
В завершение проведенного анализа и оценки целесообразно рассмотреть графическое изображение закона Фурье (рис. 3), представленное в пособии «Уравнения параболического типа и некоторые методы их решения» Е.Ф. Чупрова и Е.А. Каневой [15] с целью раскрытия взаимосвязи математической модели с реальным тепловым процессом.
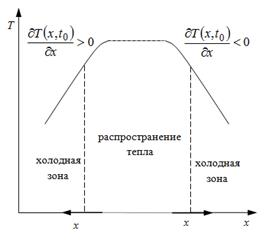
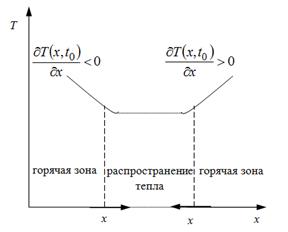
Рис. 3. Графическое изображение закона Фурье
Также на данном этапе следует записать студенту дифференциальное уравнение теплопроводности для одномерного случая, которое определяет температуру в любой точке тела и имеет вид:
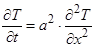 .
.
И пояснить, что 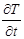 показывает скорость изменения температуры за единицу времени,
показывает скорость изменения температуры за единицу времени, 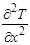 − показывает вогнутость температурного профиля
− показывает вогнутость температурного профиля 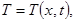
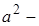 коэффициент пропорциональности, который характеризует теплоинерционные свойства тела.
коэффициент пропорциональности, который характеризует теплоинерционные свойства тела.
Затем представить графическую интерпретацию (рис. 4) данного закона [15].

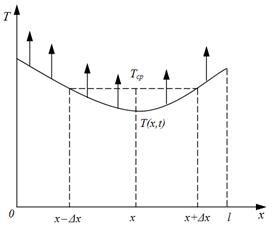
Рис. 4. Профиль температуры в момент времени t
Для того чтобы студент смог провести анализ и оценку вида температурного профиля, следует актуализировать знания о том, что выпуклость и вогнутость функции характеризует вторая производная данной функции.
Анализируя аналитическое и графическое представление данного закона, студент делает вывод о том, что если в точке с координатами 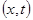 значение температуры
значение температуры 
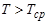 , то кривая выпукла вверх, и значит вторая производная данной функции отрицательна
, то кривая выпукла вверх, и значит вторая производная данной функции отрицательна 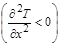 . Таким образом, температура в данной точке будет уменьшаться, следовательно, первая производная будет отрицательна
. Таким образом, температура в данной точке будет уменьшаться, следовательно, первая производная будет отрицательна 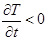 . Если же в точке с координатами
. Если же в точке с координатами 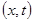 значение температуры
значение температуры 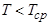 , следовательно, кривая выпукла вниз и вторая производная данной функции положительна
, следовательно, кривая выпукла вниз и вторая производная данной функции положительна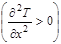 . Таким образом, температура в данной точке будет увеличиваться, следовательно, первая производная будет положительна
. Таким образом, температура в данной точке будет увеличиваться, следовательно, первая производная будет положительна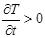 .
.
Предложенные изменения содержательной компоненты математического анализа будут способствовать подготовке студентов к анализу и оценке химико-технологических процессов в процессе обучения математике. Студенты смогут понимать математическую запись различных законов и процессов, анализировать, выделять и оценивать факторы, влияющие на процесс, что будет способствовать решению профессиональных задач.



