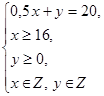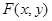В настоящее время основной идеей, положенной в основу модернизации отечественного образования, является адаптация ребенка к современным социокультурным условиям. Реализация этого тезиса в контексте ФГОС [1] предусматривает формирование универсальных учебных действий, представляющих собой метапредметные характеристики личности обучающегося, в процессе предметной подготовки. В этой связи достаточно актуальной является проблема обновления организационно-методического обеспечения предметной, в том числе и математической, подготовки обучающихся. Как показывают мониторинговые исследования, в настоящее время в образовательной практике достаточно бессистемно используются различные механизмы, направленные на формирование у обучающихся метапредметных образовательных результатов в процессе математической подготовки [2]. Для решения обозначенной проблемы целесообразно, на наш взгляд, использование игровых педагогических технологий, встроенных в процесс обучения математике.
Кроме решения обозначенной выше проблемы, использование игровых технологий [3] в процессе математической подготовки позволит повысить качество освоения тех модулей школьного курса математики, на изучение которых традиционно отводится не достаточное количество времени. Вместе с тем изучение таких разделов позволяет продемонстрировать школьникам практико-ориентированный характер математики как предметной области, показать ее связь с другими областями естествознания и обществознания. К таким модулям школьного курса математики мы относим элементы теории вероятностей, которые все шире представлены в его содержании.
Опишем некоторые организационно-методические возможности использования игровых технологий при изучении данного раздела школьного курса математики на примере урока, проводимого в виде квеста «Математика в экономике». Отметим, что игровая форма организации учебно-познавательной деятельности обучающихся позволит не только систематизировать и обобщить знания и способы деятельности по данному разделу школьного курса математики, но и будет способствовать формированию и развитию универсальных учебных действий (целеполагание, планирование, анализ, поиск и выделение необходимой информации, умение структурировать знания, участвовать в коллективном обсуждении проблем, аргументация своего мнения, учёт разных мнений учащихся и др.).
Квест проводится среди обучающихся старших классов с углублённым изучением математики (это может быть как один класс, так и несколько). Школьники случайным образом делятся на пять одинаковых по количеству человек, команд. Каждой из команд присваивается один из номеров 1, 2, …, 5, который соответствует номеру ее начальной станции. После прохождения первой из станций команда двигается по часовой стрелке (рис. 1). Шестая станция является заключительной для всех команд. Каждая команда, закончив круг из пяти станций, возвращается в свой первоначальный пункт, где из восьми предложенных заданий участники выбирают любые пять и отвечают на них по очереди (задания выбираются участниками случайным образом). Цель такой работы на заключительном этапе – выяснить, в какой степени школьники овладели теоретическим материалом, умеют ли математически грамотно и корректно формулировать определения и записывать формулы, давать математические объяснения фактам из повседневной жизни.
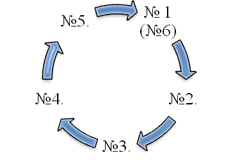
Рис. 1. Схема движения обучающихся по станциям в процессе проведения квеста
На каждой станции команде предлагается решить определенный кейс заданий [4; 5], за верное решение которого начисляется десять баллов. Команда на каждой станции может воспользоваться одной «элементарной подсказкой», которая оценивается в два балла, либо «набором подсказок» стоимостью в пять баллов. Иначе говоря, если команда воспользовалась «элементарной подсказкой», то при правильном ответе она получит только восемь баллов, если воспользуется «набором подсказок», при правильном ответе получит пять баллов. Команда, которая раньше других пройдет все станции и получит двадцать баллов, становится победителем на данной станции, вторая по времени команда, набравшая пятнадцать баллов, а также третья, имеющая в своей копилке десять баллов, становятся призерами. Система баллов начисляется таким образом, чтобы у всех обучающихся без исключения был шанс занять призовое место. При прохождении всех станций можно получить максимум семьдесят баллов.
На первой станции школьникам предлагается выполнить следующее задание: «Вы – менеджер оптового склада. Чтобы составить прогноз ближайших продаж, вам необходимо вычислить средний процент бракованной продукции. Какой будет этот процент, если доля бракованной продукции в первой партии изделий составила 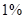 , во второй –
, во второй – 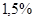 , в третьей –
, в третьей – 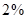 ? При этом первая партия составляет
? При этом первая партия составляет 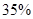 всей продукции, а вторая
всей продукции, а вторая 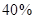 ». Ответ:
». Ответ:  . Подсказкой на данной станции может служить формула средней арифметической взвешенной, предназначенная для определения среднего процента бракованной продукции:
. Подсказкой на данной станции может служить формула средней арифметической взвешенной, предназначенная для определения среднего процента бракованной продукции:
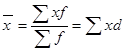 ,
,
здесь 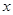 – доля бракованной продукции,
– доля бракованной продукции, 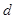 – удельный вес каждой партии в общем объеме продукции. Отметим, что элементарной подсказкой в данном задании может быть лишь название самой формулы (средняя арифметическая взвешенная), без ее написания.
– удельный вес каждой партии в общем объеме продукции. Отметим, что элементарной подсказкой в данном задании может быть лишь название самой формулы (средняя арифметическая взвешенная), без ее написания.
Для прохождения второй станции обучающимся необходимо решить задание бухгалтерского учета: «Работая бухгалтером на заводе по производству знаменитых спортивных марок одежды, Вы должны определить, как изменилось общее число отработанных чел/часов, если количество выработанной продукции увеличилось по сравнению с прошлым годом в полтора раза, а количество продукции, произведенной за 1 чел/час, повысилось на  ». Ответ на вопрос задачи: увеличилось в 1,364 раза. В наборе подсказок содержится формула
». Ответ на вопрос задачи: увеличилось в 1,364 раза. В наборе подсказок содержится формула 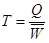 , где
, где 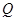 – общее количество произведенной продукции,
– общее количество произведенной продукции, 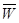 – количество продукции, произведенной за один чел/час,
– количество продукции, произведенной за один чел/час, 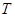 – общее число отработанное чел/часов. При этом
– общее число отработанное чел/часов. При этом 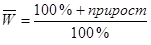 .
.
На третьей станции обучающиеся выступят в роли сотрудников центра маркетинговых исследований, которым поручили провести статистическую обработку данных по наличию работоспособного населения: «По трем населенным пунктам имеются данные, представленные в таблице 1. Необходимо определить среднее значение каждого признака».
Таблица 1
Данные о трудоспособном населении в трех населенных пунктах
|
Название населенных пунктов |
Общее число жителей (тыс. чел.) |
Лица старше 18 лет (в процентном соотношении) |
Лица старше 18 лет, занятые в общественном производстве (в процентном соотношении) |
|
|
|
|
|
|
Абакан |
180 |
60 |
70 |
|
Черногорск |
60 |
69 |
75 |
|
Саяногорск |
50 |
54 |
83 |
Ответ на вопрос задачи: 81,7; 60,1; 75,5. В наборе подсказок будут следующие формулы:
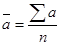 (простая средняя арифметическая),
(простая средняя арифметическая),
где 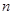 – число населенных пунктов.
– число населенных пунктов.
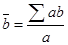 (взвешенная средняя арифметическая).
(взвешенная средняя арифметическая).
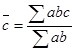 (взвешенная средняя арифметическая).
(взвешенная средняя арифметическая).
В качестве элементарной подсказки может выступать, соответственно, одна из формул.
На следующей станции предлагается сюжетная задача: «Вам необходимо заказать 5 упаковок по 6 л яблочного сока в бар. Необходимо принять решение, продолжать сотрудничать с прежним поставщиком 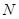 либо найти нового, если при анализе себестоимости единицы продукции Вы получили среднюю себестоимость
либо найти нового, если при анализе себестоимости единицы продукции Вы получили среднюю себестоимость 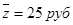 ,
, 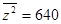 . Определите коэффициент вариации себестоимости. Поменяете ли Вы поставщика, если нормальный коэффициент вариации себестоимости равен
. Определите коэффициент вариации себестоимости. Поменяете ли Вы поставщика, если нормальный коэффициент вариации себестоимости равен 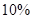 ?». Ответ: коэффициент вариации себестоимости поставщика
?». Ответ: коэффициент вариации себестоимости поставщика 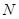 равен
равен 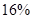 , следовательно, меняем поставщика. В наборе подсказок будут формулы коэффициента вариации себестоимости и среднего квадратичного отклонения:
, следовательно, меняем поставщика. В наборе подсказок будут формулы коэффициента вариации себестоимости и среднего квадратичного отклонения:
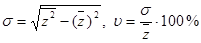 ,
,
здесь 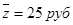 – средняя себестоимость единицы продукции;
– средняя себестоимость единицы продукции; 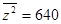 – среднее из квадратов индивидуальных значений.
– среднее из квадратов индивидуальных значений.
Пятую станцию обучающимся предлагается пройти, воспользовавшись персональным компьютером с использованием Microsoft Excel [6]. Задача звучит следующим образом: «Вам предлагается рассчитать самый дешевый рацион кормления сельскохозяйственных животных, если предполагается, что рацион коров состоит из двух видов кормов: сена и концентратов. Суточное потребление кормов на одну корову равно 20 кормовых единиц. В таблице 2 приведены числовые данные о себестоимости кормов в данном хозяйстве.
Таблица 2
Себестоимость кормов
|
Виды кормов |
Содержание кормовых единиц в 1 кг кормов |
Себестоимость кормов, в коп. |
|
Сено |
0,5 |
1,5 |
|
Концентраты |
1,0 |
2,5 |
Заметим, что ежедневный рацион кормления сельскохозяйственных животных должен включать не менее 16 кг сена. Бланк для выполнения задания на бумажном носителе представлен в таблице 3.
Таблица 3
Бланк для выполнения задания
|
|
|
|
Система ограничений |
|
|
Целевая функция |
|
Оценивание ответа на поставленный вопрос на данной станции зависит от правильности прохождения следующих этапов решения задачи.
1. Правильно составлена система ограничений (2 балла).
2. Правильно задана целевая функция (2 балла):
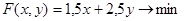 .
.
3. Правильно занесены формулы в таблицу (рис. 2) (3 балла):
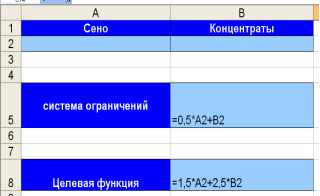
Рис. 2. Оформление формул с использованием электронной таблицы
4. Правильно заполнено диалоговое окно «Поиск решения» (рис. 3) (3 балла):
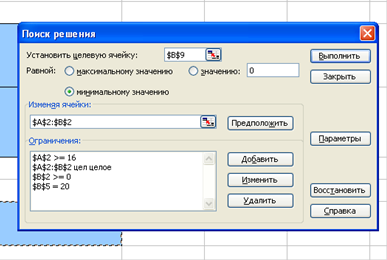
Рис. 3. Окно «Поиск решений» в электронной таблице
Набором подсказок будет служить инструкция с действиями на каждом этапе.
Шестая станция является заключительной для каждой из команд. Команда, закончив круг из пяти станций, возвращается в свой первоначальный пункт, где из восьми предложенных вопросов (рис. 4) участники выбирают любые пять, как это было описано выше.

Рис. 4. Карточки с вопросами
Никаких подсказок на станции нет, за каждый правильный ответ команда получает 2 балла, за неполный ответ – 1 балл, за неверный ответ или отсутствие ответа – 0 баллов.
В конце игры подводятся итоги и награждение победителей.
В заключение стоит добавить, что данная форма организации учебно-познавательной деятельности учащихся может применяться на уроках при изучении различных тем школьного курса математики. Главное условие ее использования – наличие сюжетной линии, чтобы после прохождения квеста обучающиеся имели представление, в какой сфере жизни и в каких конкретно ситуациях они могли бы применить полученные математические знания, умения и способы деятельности метапредметного характера.
Помимо описанного выше квеста, нами были также реализованы в образовательной практике некоторых школ региона такие квесты, как «Функция и области ее использования» и «Геометрический и физический смысл производной». Не стоит забывать, что применение ИКТ, в частности интерактивной графики, таких сервисов, как Prezi.com, Zoom презентаций, и т.п., не только будет способствовать реализации принципа наглядности, но и повысит интерес обучающихся к математике при описанной форме организации учебно-познавательной деятельности обучающихся.





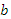
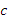
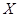 (кг) – масса сена в день,
(кг) – масса сена в день,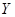 (кг) – масса концентратов в день
(кг) – масса концентратов в день