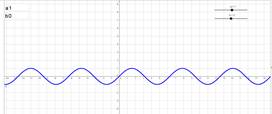
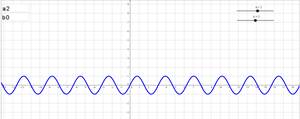
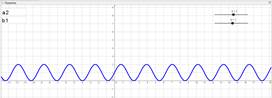
Информационные технологии позволяют переосмыслить применение Интернета в учебном процессе: от получения доступа к образовательным материалам различного вида (текстовым, визуальным, мультимедийным) до выполнения работы совместно с преподавателем или группой [1]. Быстро развивающиеся сервисы облачных вычислений предоставляют широкий спектр полезных приложений в обучении. Использование облачных сервисов и программы динамической геометрии рассмотрим на примере изучения темы «Простейшие преобразования графиков», которая предполагает следующие этапы обучения:
- Изучение новой темы с использованием программы GeoGebra.
- Тестирование, после которого проводится диагностика усвоения материала обучающимися, что позволяет подобрать каждому из них индивидуальные задания, направленные на устранение недостаточно изученных разделов темы. Это позволяет индивидуализировать самостоятельную деятельность, что способствует более эффективному овладению материалом.
- На основе результатов тестирования составляются совместно со обучающимися индивидуальные практические задания. Обучающимся предлагаются индивидуальные самостоятельные работы, формой контроля может служить web-проект, выполненный в среде GeoGebra и размещенный на персональной странице.
Знакомство с простейшими преобразованиями графиков начинается в 7 классе при изучении темы «Взаимное расположение графиков линейных функций». В 8 классе рассматриваются функции 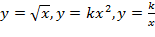 , построение и преобразование их графиков функций. С помощью преобразований строятся функции вида
, построение и преобразование их графиков функций. С помощью преобразований строятся функции вида 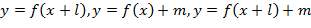 . При этом каждое преобразование изучается отдельной темой, в результате чего у обучаемых не формируется целостное представление о преобразованиях. А в 9 классе к этому списку добавляются и числовые функции, на примере степенных функций и функции вида
. При этом каждое преобразование изучается отдельной темой, в результате чего у обучаемых не формируется целостное представление о преобразованиях. А в 9 классе к этому списку добавляются и числовые функции, на примере степенных функций и функции вида 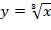 , что окончательно запутывает обучаемых. В то же время выполнение простейших преобразований графиков необходимо при решении различных задач, в частности при нахождении области определения или множества значения функции, а также при решении уравнений и систем уравнений графическим методом [2].
, что окончательно запутывает обучаемых. В то же время выполнение простейших преобразований графиков необходимо при решении различных задач, в частности при нахождении области определения или множества значения функции, а также при решении уравнений и систем уравнений графическим методом [2].
Целесообразнее всего будет изучать все возможные преобразования графиков одновременно. Для этих целей наиболее эффективным средством изучения являются программы динамической геометрии.
Возможности применения программ динамической геометрии многочисленны. При помощи данных программ можно создавать заготовки с заданиями и высылать на электронные адреса учащихся или публиковать на сайте с разграничением доступа обучающихся. Также можно использовать апплеты при рассмотрении темы, создавая динамические построения геометрических объектов. Программа имеет возможность просмотра хода построений и выполнения задания, что позволяет выявить правильность выполнения учащимися построения или решения задачи и определить, чему из пройденного материала следует больше уделить внимание. Эффективнее всего будет создание коллекции апплетов на каждую из тем, причем в создании данной коллекции могут принимать участие и сами обучающиеся [3].
Для наших задач наиболее подходящим решением является свободно распространяемая программа GeoGebra.
У программы GeoGebra:
- хорошо продуманный интерфейс;
- совмещает в себе возможности выполнения построений и аналитическую геометрию;
- встроенный язык, при помощи которого можно задавать построения и производить математические расчеты;
- активное сообщество пользователей по всему миру (190 стран), институты GeoGebra [4].
Перечислим основные возможности программ динамической геометрии:
- строить точки, прямые, лучи, отрезки, окружности;
- построение комбинаций базовых фигур: углы, многоугольники, части круга и пр.;
- построение отрезков и углов заданной величины;
- предоставление инструментов для построения перпендикулярных и параллельных прямых, а также биссектрисы угла;
- выполнение параллельного переноса, симметрии, поворота и гомотетии фигур;
- деформирование фигуры или отдельных её частей;
- вычисление длины отрезка, величины угла, периметра и площади многоугольников, длины окружности и площади круга;
- осуществление анимации фигуры или отдельных её точек;
- выполнение итерации с геометрическими и алгебраическими объектами [4].
Рассмотрим возможности применения программы GeoGebra при изучении темы «Простейшие преобразования графиков».
Для того чтобы правильно построить график какой-либо функции, нужно сначала распознать заданные в формуле преобразования. Каждое отдельно взятое математическое действие в формуле задаёт отдельный вид преобразований. Поэтому сколько в формуле действий, столько и преобразований нужно будет выполнить над графиком элементарной функции. GeoGebra позволяет моментально изобразить преобразования графика при изменении параметров преобразования.
Например, дана функция: y=(x+2)2–3 [5].
Для того чтобы построить график этой функции, надо сначала построить график функции y=x2, затем переместить ее на 2 единицы влево по оси абсцисс и на 3 единицы вниз по оси ординат, следовательно, для наглядности построения нужно построить три графика, что перегружает чертеж и путает учащихся. А в том случае, когда поменяется хотя бы один из параметров, приходится перечертить весь график, что весьма не эффективно и отнимает массу времени. Все эти проблемы можно решить, используя программу GeoGebra. Для того чтобы изобразить преобразования графика функции y=(x+2)2–3 в GeoGebra, нужно всего лишь построить график y=(x+a)2–b при начальных значениях a=0 и b=0, затем, изменяя значения параметров a и b, следить за преобразованиями графика данной функции, при этом если построить график функции y=(x+a)n–b, можно менять еще и значение показателя данной функции, что еще больше углубит знания о преобразованиях функции при изменении различных параметров (рис. 1).
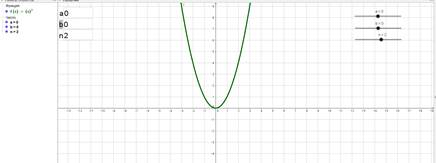
Функция y=(x+a)n+b при n=2, a=0, b=0
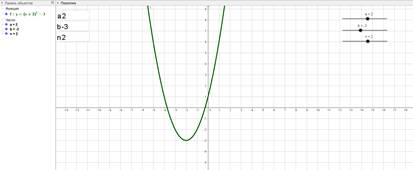
Функция y=(x+a)n+b при n=2, a=2, b=3
Рис. 1. Преобразование графика функции y=x2
Для того чтобы изменить параметры, следует всего лишь ввести значение параметра и нажать клавишу «Enter» или передвинуть ползунок в соответствующее положение, при этом график моментально отображает заданное преобразование. Это позволяет наглядно и оперативно показывать преобразования графика, не тратя время на лишние построения. Преимуществами применения GeoGebra при построении данного графика являются: точность построения, чего невозможно добиться при изображении графика на обычной доске, а также возможность моментального изменения функции (например, квадратной на кубической или четвертой степени и т.д.), не тратя время на новые построения (рис. 2) [6].
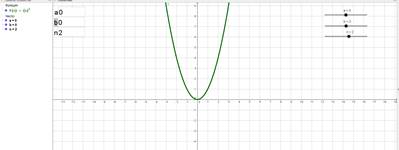
Функция y=(x+a)n+b при n=2, a=0, b=0
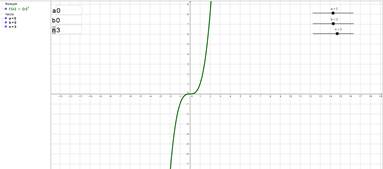
Функция y=(x+a)n–b при n=3, a=0, b=0
Рис. 2. Преобразование графика функции y=xn
Соответственно тут же можно показать преобразования данного графика при изменении соответствующих параметров.
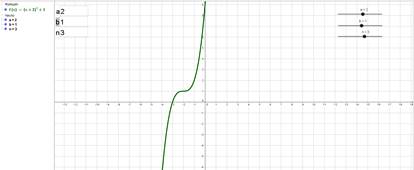
Рис. 3. Функция y=(x+a)n–b при n=3, a=2, b=1
Так же можно изобразить график любой функции. Например, нужно показать преобразование функции y=sinx. Выполним преобразование вида y=sin2x+1. Для того чтобы построить график этой функции, надо сначала построить график функции y=sinx, затем переместить ее на 1 единицу вверх по оси ординат, а умножение аргумента на 2 сжимает синусоиду в два раза. Для построения данного графика необходимо построить график функции y=sinax+b при начальных значениях a=0 и b=0, затем, изменяя значения параметров a и b, следить за преобразованиями графика данной функции. Пошаговое изменение параметров позволяет выявить как ведет себя график при том или ином значении параметра, что способствует усвоению влияния параметров преобразования на графике и свойствах самой функции. Таким образом, становится понятно, что для получения графика y=sin2x+1 необходимо сделать два преобразования (рис. 4):
- умножение на 2 – сжимает синусоиду в два раза;
- прибавление 1 – поднимает синусоиду на одну единицу.
Проделав данные преобразования, получаем график искомой функции, попутно рассмотрев свойства и графики промежуточных функций. Данную заготовку также можно использовать для рассмотрения других преобразований, не тратя время на дополнительные построения, что экономит время на занятии и при подготовке к нему. Использование GeogGebra придает красочность и точность чертежу.
Рассматривая данные примеры, учащиеся сами могут прийти к выводу, что все преобразования можно разделить на:
- растяжение от оси Ox или сжатие к оси Ox;
- преобразование симметрии относительно оси Ox;
- параллельный перенос вдоль оси Ox;
- растяжение от оси Oy или сжатие к оси Oy;
- преобразование симметрии относительно оси Oy;
- параллельный перенос вдоль оси Oy.
Таким образом, рассмотрение данных примеров сходится к нахождению основной функции и выявлению преобразований, произведенных над ней [7].
|
Функция y=sinax+b, при a=1, b=0 |
Функция y=sinax+b, при a=2, b=0 |
|
Функция y=sinax+b, при a=2, b=1 |
|
Рис. 4. Преобразование графика функции y=sinx
Построив таким образом несколько графиков, можно скрывать с чертежа и возвращать назад на экран сразу несколько изображений посредством панели объектов, которая находится в левой части окна программы.
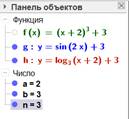
Рис. 5. Панель объектов программы GeoGebra
Данная функции программы GeoGebra позволяет сравнить график логарифмической функции с другими, например с показательной. И учащиеся наглядно видят, что логарифмическая и показательная функции являются взаимно обратными (рис. 6).
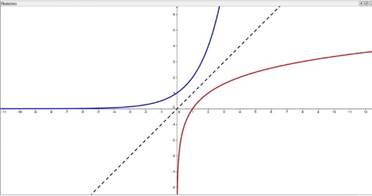
Рис. 6. Взаимно обратные функции
Очевидно, что подобным образом можно рассматривать и другие функции. При этом на полотно графики удобно выводить по одному, чтобы учащиеся сами приходили к выводу [8].
Знакомство с новым материалом, таким образом, становится более увлекательным и наглядным, учащиеся с удовольствием участвуют в проведении урока и отмечают изменившиеся свойства функции.
Использование программы GeoGebra ускоряет процесс обучения, позволяет точно и наглядно изображать преобразования графиков различных функций и дает возможность учащимся участвовать в процессе обучения, при этом экономя время на лишние построения. Также следует отметить, что данная методика развивает не только математические познания, но и навыки использования новых информационных технологий, что является важным критерием для современного выпускника. Использование GeoGebra не следует ограничивать только при проведении лекции, можно дать домашнее задание: построение различных графиков функции и их преобразований в программе GeoGebra, что будет способствовать закреплению изученного материала.
После изучения новой темы обучающиеся переходят ко второму этапу тестирования с применением сервиса UzTest (рис. 7), имеющего средства диагностики решений, которые позволяют оценить уровень усвоения нового материала и подобрать соответствующие индивидуальные задания (рис. 8).
Выполнение индивидуальных заданий позволяет оценить результаты самостоятельной деятельности обучающегося и определить уровень освоения новой темы и сформированности самостоятельной деятельности.

Рис. 7. Пример теста в среде UzTest
Измерение эффективности обучения осуществлялось:
- на основе балльно-рейтинговой системы оценивания знаний;
- по результатам процентного соотношения правильно решённых задач к общему числу предложенных задач [9].
При этом сравнивались два класса учащихся, один из которых пользовался облачными технологиями и программой GeoGebra в обучении, а второй – нет.
Оценка эффективности методов обучения с применением перечисленных технологий происходила в сравнении с традиционными методами и заключалась в измерении результатов обучения, учитывая и затраты времени учащихся.
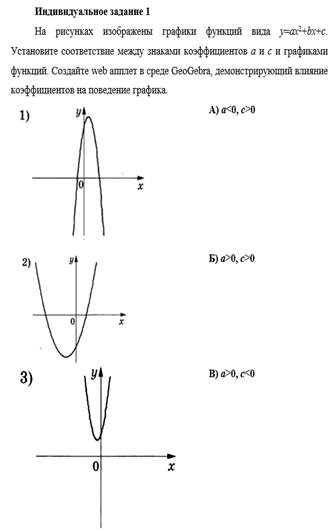
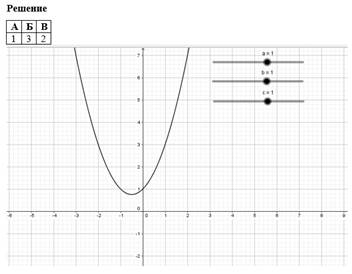
Рис. 8. Пример индивидуального задания
Результаты проведенного эксперимента показали, что применение облачных технологий и возможностей программы GeoGebra позволяет повысить объективность контроля знаний учащихся — на 20-25%, а эффективность практических занятий по математическим дисциплинам не менее чем на 30%. Успеваемость в экспериментальных классах, применяющих в обучении данные технологии, выше в среднем на 15-20%.
Таким образом, применение возможностей программы GeoGebra облегчает организацию самостоятельной деятельности обучающихся и контроль над ее результатами, а также повышает усвоение материала и наглядность построения графиков, что способствует повышению уровня образования. При этом созданный сайт и заготовки можно использовать неоднократно на протяжении всего учебного года и с различными группами учащихся, добавляя новые страницы на сайт со ссылками на файлы заданий. Следовательно, описанная методика является эффективной и мощной педагогической технологией для всего учебного процесса.