Модернизация образования в России определяет новые подходы к обновлению и развитию всей образовательной системы, в том числе и математическому образованию, его содержанию, методам и организации его освоения учеником, созданию условий для развития личности ученика.
В современных образовательных стандартах именно личностные и метапредметные результаты, связанные с развитием личности ученика, занимают важное место в образовательных результатах. Но, несмотря на развивающую направленность школьного образования, как показал проведенный нами анализ кандидатских и докторских диссертаций за последние 30 лет, в исследованиях по методике обучения математике меньше всего работ, посвященных именно развитию учащихся.
Для сравнения на рисунке 1 представлены графики, отражающие направленность методических диссертаций: диссертации, приоритетной целью исследования которых является развитие мышления и других психических процессов; диссертации, основная цель исследования которых – улучшение процесса освоения учениками математики; диссертации, направленные на развитие личностных качеств (для краткости цели обозначены как воспитательные).
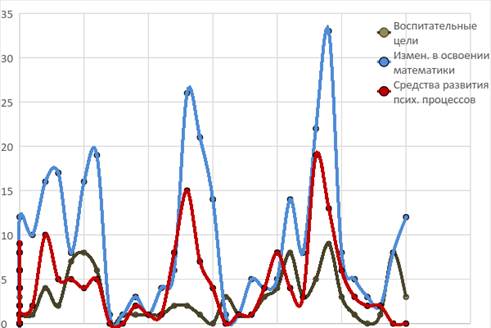
Рис.1. Графики, отражающие направленность методических диссертаций
Но, как показывает история развития математического школьного образования, внимание именно к развивающему аспекту обучения дает значимые результаты. Так, в 1932 г. школы в очередной раз переходят на новые программы. В них предлагалось отразить «точно очерченный круг систематизированных знаний». Главной целью стало «всестороннее гармоническое развитие личности» [1, с. 156], которая оставалась основной до 1951 г., когда появилась цель подготовки учащихся к поступлению в вуз. Как результат реализации постановления и программы – повсеместное резкое повышение качества образования, в частности уровня математической (и не только) грамотности. Престиж науки и образования в это время был высок, профессия учителя – значима. За 1950–1960-е гг. (а это ученики, осваивавшие учебные предметы по этой программе) было сделано 80% научных открытий периода 1950–1990 гг. Запуск первого спутника и полет человека в космос заставили американцев обратиться к русскому феномену. Они сделали вывод: «русские выиграли космос за ученической партой».
Таким образом, направленность на всестороннее развитие учащихся способствует решению социальных задач, которые ставят перед школой государство и общество. Но согласно ФГОС ОО проблема развития учащихся должна решаться через освоение универсальных учебных действий и межпредметных понятий, которые заданы метапредметными результатами. При этом в качестве средства их достижения образовательные стандарты предлагают рассматривать учебно-познавательные и учебно-практические задачи. Анализ литературы показал, что нет описания четких характеристик учебно-познавательной задачи (УПЗ). В данной статье мы попытались выделить критерии таких УПЗ, которые направлены на развитие учеников и могут быть использованы при обучении математике. Анализ УПЗ, встречающихся в методических публикациях, позволяет разделить их на задачи, которые рассматриваются внутри учебного предмета, и те, решение которых требует привлечения знаний и умений из других учебных предметов или жизненного опыта [5].
Развитие предполагает решение проблем, поэтому рассматриваемые задачи должны содержать проблему. Но решение проблемы возможно при наличии желания ученика ее решать, его смотивированности. Как показал нейрофизиолог Д. Соуза [4], наибольшую мотивацию обеспечивает связь нового материала с окружающим ребенка миром, с другими учебными предметами. Это отмечали и сами ученики в проведенном НИИ общего образования РГПУ им. А.И. Герцена анонимном опроснике [2]. Поэтому в качестве средства развития учащихся были выбраны метапредметные учебные задачи и задания, в содержании которых заложено требование или предписание учащимся решить проблему, с которой они могут столкнуться в реальном мире или на стыке разных учебных предметов. Это характеризует задачу как метапредметную («выходящую» за пределы учебного предмета). В ходе решения учащиеся открывают ранее не известное для них знание, и не только в пределах математики, а также овладевают обобщенными методами и приемами, т.е. решение задач дает новый личностный прирост в познавательном аспекте.
Одним из значимых для учеников качеств личности является успешность в социуме. Как необходимое условие успешности психологи выделяют владение коммуникативными умениями, поэтому рассматриваемые задачи должны позволять обсуждать возможные решения и ответы и активизировать процесс «думания», что возможно при рассмотрении разных точек зрения. Значит, задачи должны содержать проблему и отличаться неоднозначностью рассматриваемой ситуации, ответа или решения.
Таким образом, основными критериями рассматриваемых нами задач, способствующими развитию ученика, являются:
1) метапредметность;
2) проблемность;
3) познавательность (или новизна информации);
4) неоднозначность, создающая «коммуникативное поле» для обсуждения.
Рассмотрим одну из таких задач [3].
Задача. Перед вами два рисунка. Из каких произведений герои на них? Кто авторы?

Чем отличаются жертва Черномора и Дюймовочка от обычных людей?
Почему нет людей таких размеров, как вы думаете?
Ученики предлагают разные варианты. Учитель наводит их на научный вывод, предложив подсказки.
1. Подумайте, почему ноги слона имеют такую толщину.
2. Масса, которую может выдержать кость человека, зависит от ее прочности. Найдите информацию в интернете.
3. От чего зависит масса человека? Что произойдет с ней при увеличении в a раз?
Или учитель может предложить информацию (дана ниже со вспомогательными задачами на листках).
Известно, что прочность кости человека 170 Н/мм2. Чтобы найти массу, которую может выдержать кость, надо прочность умножить на площадь поперечного сечения и разделить на g (g = 9,8 Н/кг). Кость голени человека имеет площадь поперечного сечения 2,8 см2. Какую массу она может выдержать? (Ответ: 4760 кг)
Допустим, мы увеличиваем рост человека в 10 раз. При увеличении роста и сохранении пропорций масса тела увеличивается пропорционально объему тела, который возрастает в кубической зависимости от линейных размеров тела. Масса увеличится в 1000 раз. Что касается прочности кости, то она увеличивается пропорционально площади ее поперечного сечения, которая от линейных размеров зависит квадратично. Так, при увеличении роста человека в 10 раз площадь поперечного сечения кости голени увеличится только в 100, т.е. есть прочность кости станет в 10 раз меньше. Гигант просто не сможет стоять на ногах, они сломаются. Чтобы не сломались, их площадь поперечного сечения нужно увеличить в 10 раз.
Это задание можно предложить ученикам как мотивационное на этапе введения новой темы, а именно при ознакомлении учащихся с новым видом функциональной зависимости – квадратичной или кубической.
После работы с информацией ученикам целесообразно предложить нарисовать человека с увеличенным ростом, но держащего свое тело на ногах.

Вот так будет выглядеть этот человек.
Что касается личностных результатов, то во ФГОС ОО указано, что личностные результаты должны отражать формирование учебно-исследовательской, творческой и иной деятельности. Такая деятельность подразумевает развитие исследовательской компетенции.
Исследовательская компетентность школьника – это способность и готовность учащегося самостоятельно осваивать и получать новые знания, выдвигать идеи, гипотезы в результате выделения проблемы, работы с различными источниками знаний, исследования темы, проведения наблюдения (опыта, эксперимента и т.д.), предложение путей решения проблемы и поиска наиболее рациональных вариантов решения вопросов, проектов. Для ее формирования часто используются исследовательские задачи. Необходимо отметить, что не всегда можно четко разграничить исследовательские задачи и учебно-познавательные задачи, так как некоторые исследовательские задачи будут удовлетворять критериям учебно-познавательных.
При традиционном подходе ученики решают отдельные задачи, их оценивает учитель, и учитель же предлагает новую задачу. При этом задачи рассматриваются однозначные (с однозначным восприятием задачной ситуации и одним ответом). Но реализация ФГОС ОО требует иного подхода. При исследовательском же подходе ученик сам ставит вопросы и ищет на них ответы, выдвигает гипотезы, доказывает и опровергает их. Всякий полученный ответ может стать основанием для новых вопросов. Результат может быть не известен и самому учителю заранее. Ученик учится, размышляя и исследуя.
При работе с исследовательскими задачами ученикам неизбежно приходится иметь дело с математическими методами, поэтому исследовательские задачи могут стать частью обучения математике.
К основным характеристикам исследовательских задач, направленных на развитие ученика, можно отнести следующие.
1. Направлены на:
1) поиск обобщающего способа решения;
2) определение методов решения проблемы;
3) нахождение достаточных условий;
4) нахождение достаточных и необходимых условий для выполнения определенных действий или существования объекта, или определенного количества ответов, и т.п.
2. Предполагают рассмотрение неоднозначных ситуаций и, как следствие, наличие более одного ответа.
Исследовательский характер заданий позволяет переработать изученный материал, применить его в новых условиях, а, значит, раскрыть в полной мере смыслы изучаемых понятий. Добавление требования использовать в тексте задачи и при решении разные способы представления информации будет способствовать ее пониманию. Задачи исследовательского характера могут быть предметными и метапредметными. Именно метапредметные задачи позволяют реализовать связь с окружающим ребенка миром, с другими учебными предметами, а значит, будут «работать» на обеспечение мотивации, что необходимо и для развития ученика, и для усвоения математики. Ведь связь с окружающим миром, с опытом ребенка является одним из необходимых условий демонстрации значимости изучаемого материала. Именно практикоориентированность нейрофизиологи относят к основному механизму демонстрации значимости учебного материала, а значит, и обеспечения мотивации (Д. Соуза).
Задания исследовательского характера существенно отличаются от традиционных заданий уже своей формулировкой. В их формулировках нет явного ответа, его необходимо найти самим ученикам и обосновать.
При решении исследовательских задач у учащихся часто возникают затруднения, поэтому учителю следует задавать наталкивающие вопросы и учить этому учеников. Уметь задавать вопросы – одно из важнейших умений, так как умело заданный вопрос создает условия для правильного и конкретного ответа.
После решения задач исследовательского характера необходимо, чтобы учащиеся осуществляли исследование ответа, вывода (т.е. ставили вопрос о существовании решения, о числе решений, об особых случаях, какие могут представиться) при рассмотрении каждой задачи, особенно такой, которая предлагается в общем виде.
Для развития творческого мышления нужно постепенно формировать у учащихся умение определять, какие частные случаи необходимо выделить впоследствии.
Приведем пример исследовательской задачи, в которой практикоориентированность, связь с окружающим миром предлагается через использование исторической справки задачи.
Задача. Историческая справка.
Время появления крепостных башен относится к самой глубокой древности; по дошедшим до нас изображениям башни строили древние египтяне, ассиро-вавилоняне и финикийцы.

В письменных памятниках Древней Греции и Древнего Рима встречается не только упоминание, но довольно подробное описание подобных башен. Римляне начали располагать свои башни не только на крепостной ограде, но и вне крепостей, в виде передовых укреплений в горных проходах, у переправ через реки, а также на границах, как сторожевые посты. Они же ввели полевое применение башен как опорных пунктов своих лагерей и как наблюдательных вышек на полях сражений.
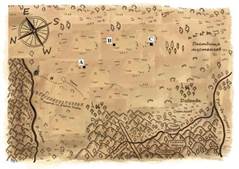
Задача.
В средние века оборонительные крепостные башни получили большое развитие в Западной Европе при укреплении замков. Рыцарю, во владениях которого были три оборонительные башни, потребовалось построить еще одну башню для защиты своей территории. Он приказал своим работникам найти подходящее место для башни. При этом должно выполняться одно условие: все четыре башни в ансамбле должны образовывать параллелограмм. Выполните построение требуемого объекта на карте.
(Ученикам предлагается рассмотреть план местности, на котором необходимо выполнить построение).
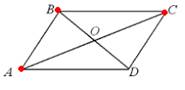
Рассмотри первый и второй этап решения задачи, в которых закладываются эта неоднозначность и направления этапа исследования, что отличает предлагаемые исследовательские задачи от традиционных задач на построение.
I. Анализ
|
Вопросы к ученикам (в скобках даны ответы на вопросы) |
Содержание этапа |
|
1) Что нам нужно построить, чтобы получился параллелограмм? (4-ю вершину и стороны) 2) Какие элементы параллелограмма уже имеются? (3 вершины) 3) Какие еще элементы можно сразу построить? (2 стороны) Какие? (АВ, ВС) 4) Почему не АС и ВС? (Исследование!) 5) Как мы можем получить 4-ю вершину? 6) Какие элементы параллелограмма еще не указаны на рисунке? (диагонали) |
Пусть задача решена, тогда имеем параллелограмм с вершинами в точках A, B, C, D
АВ||СD; BC||AD; АВ=СD; BC=AD; (исследование!) BD и AC – диагонали AO=OC и BO=OD |
В начале работы на данном этапе учащиеся абстрагируются от реальных объектов и моделируют ситуацию с помощью геометрических фигур на вспомогательном чертеже, что способствует развитию такого исследовательского умения, как моделирование. С помощью вопросов учителя или самостоятельно с помощью тех свойств, которые были выписаны на доске в задании 2) на этапе актуализации, учащиеся формулируют гипотезу и конструктивные свойства точки, которую надо построить. При решении этой задачи уже на этапе анализа могут быть выделены три варианта решения.
|
Этап |
Вариант 1 |
Вариант 2 |
Вариант 3 |
|
Анализ |
D=l1 |
D= |
BD и AC – диагонали BO=OD и AO=OC |
Учителю следует обратить внимание учащихся на то, что от выбора пути решения задачи уже на этапе анализа зависит способ решение на остальных этапах. Как только у учеников появляются разные версии по поводу решения задачи, необходимо дать им свободу выбора, чтобы они реализовали то решение, которое они считают наиболее целесообразным. На уроке может быть выбран один путь решения задачи, а остальные даны на самостоятельное решение в качестве домашнего задания.
На этом этапе особое внимание уделяется развитию таких исследовательских умений, как: моделирование; абстрагирование; выдвижение гипотезы; анализ и развитие вариативности мышления.
II. Построение
Цель этапа:
- написание алгоритма построения искомой фигуры;
- ее непосредственное построение.
Суть этапа
В содержании второго этапа решения задач на построение мы выделили две части:
1) перечисление в определенном порядке всех элементарных построений, которые нужно выполнить согласно анализу для решения задачи;
2) непосредственное выполнение этих построений на чертеже при помощи чертежных инструментов.
Действительно, решить задачу с помощью тех или иных инструментов — значит указать конечную совокупность элементарных, допустимых для данных инструментов построений, выполнение которых в определенной последовательности позволяет дать ответ на вопрос задачи.
Ознакомление с данным этапом осуществляется при решении самой первой задачи на построение, которой обычно является задача о построении отрезка, равного данному, на данном луче с концом в начале этого луча. В беседе, сопровождающей введение этапа, необходимо отметить, в чем состоит решение любой задачи на построение, и указать, что осуществление этого этапа как раз и состоит в перечислении конечного числа операций построения искомой фигуры.
Результат этапа построения:
- чертеж искомой фигуры;
- описание алгоритма ее построения.
Поиск различных способов решения задачи и доказательства теорем является основным приемом, способствующим развитию вариативного мышления школьников. В процессе поиска учащиеся наглядно убеждаются, что при решении той или иной задачи можно устанавливать различные связи и отношения между компонентами и в зависимости от этого получать различные способы решения. Эти способы могут быть как более, так и менее эффективными. Сопоставляя и сравнивая их, можно выбирать наиболее рациональный подход к решению задачи. Это способствует развитию такого исследовательского умения, как планирование. При этом эффективно формируется такое умение, как систематизация, так как необходимо оценить выбор того или иного способа построения с точки зрения разных оснований, т.е. выгодно ли выполнять построение из-за простоты шагов построения или потому, что в этом случае доказательство будет содержать меньше шагов.
Оба эти вида задач и заданий способствуют развитию поисковых умений ученика и логических УУД и в конечном счете «работают» на развитие ученика.