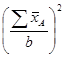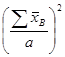Млекопитающие являются практически значимой группой животных, представленной во всех биотопах, природных зонах и подзонах всего поволжского региона. Являясь консументами в цепях питания, они занимают почти все трофические уровни, кроме первого. В пределах Нижегородского региона к консументам первого порядка (растительноядные) относится 29 видов млекопитающих (41,4 %), среди которых преобладают наиболее многочисленные и широко распространенные виды. К консументам второго порядка (смешанный тип питания) относятся 16 видов (22,9 %), которые малочисленны и распространены локально. Консументы третьего порядка (плотоядные) насчитывают на территории области 25 видов (35,7 %), численность которых, как правило, невелика, и распределены они по территории достаточно равномерно [10].
Немаловажным практическим аспектом млекопитающих является их участие в поддержании зоонозных инфекционных болезней. Особенно это характерно для мелких млекопитающих, доля которых составляет более 60 %. Большинство из них в той или иной степени являются носителями целого ряда инфекционных болезней, в которые может вовлекаться и человек. В частности, из группы протозойных болезней отмечаются пироплазмозы, нутталиозы, анаплазмозы, кокцидозы и саркоспоридиозы. Из группы бактериальных болезней обычны лептоспирозы, сальмонеллезы, риккетсиозы, туляремия, сапронозы и токсоплазмозы. Из группы вирусных болезней отмечены бешенство, ГЛПС, клещевой энцефалит и некоторые другие. И, наконец, практически все млекопитающие являются носителями обширной группы гельминтозов, вызываемых плоскими и круглыми червями.
Териофауна Нижегородской области включает 76 видов млекопитающих из 6 отрядов. Наименьшим числом представителей характеризуются отряды зайцеобразных (2 вид) и парнопалых (4 вида); несколько шире представлены насекомоядные (11 видов), рукокрылые (12 видов) и хищные (16 видов). Наибольшим видовым разнообразием выделяется отряд грызунов (31 вид). Такое соотношение видов и довольно высокое разнообразие териофауны в целом, согласуется с положением региона в двух природных зонах: лесной и степной, а также отражает специфику хозяйственного освоения природных ресурсов [3]. В Нижегородской области представлены две природные зоны (лесная и степная) и три подзоны (южнотаежная, смешанных лесов и лесостепная) [1].
Цель исследования
Цель настоящей работы заключается в развитии методологии дисперсионного подхода к анализу различных жизненных проявлений живых организмов и специфике воздействий на них факторов окружающей среды.
Материалы и методы исследования
Материал по мелким млекопитающим, в упомянутых выше подзонах, был собран и обработан на протяжении 1990–2008 гг. В состав южнотаежной подзоны входит северное Заволжье Нижегородской области на юг до линии: Варнавино – Урень – Шаранга. Здесь распространен таежный фаунистический комплекс млекопитающих из 11 видов. Лесостепная подзона, в значительной степени трансформированная антропогенной деятельностью, включает в свой состав юг и юго-восток Предволжья на север до линии: Дивеево – Арзамас – Лысково. Здесь представлен лесостепной фаунистический комплекс млекопитающих из 8 видов. Остальная территория области представлена подзоной смешанных лесов, в пределах которой распространен соответствующий фаунистический комплекс, насчитывающий 34 вида.
Следует отметить, что во всех трех рассматриваемых подзонах, в той или иной степени представлены широколиственные леса, сильно измененные антропогенной деятельностью с соответствующим фаунистическим комплексом из 9 видов. На примере двухфакторного неравномерного дисперсионного комплекса проанализирована относительная численность сообществ мелких млекопитающих по четырем основным биотопам представленных в трех подзонах Нижегородской области. Отработано около 20 000 ловушко/суток и выловлено 4 000 особей мелких млекопитающих. Численность зверьков определялась по общепринятым методикам [5].
Результаты исследования и их обсуждение
Дисперсионный анализ дает количественную оценку силы воздействия фактора и ее достоверность. При необходимости дисперсионный анализ позволяет в значительной степени расширить и углубить методику корреляционного анализа, выявляя воздействие одного признака на другой [7, 8]. Основная особенность всех приемов дисперсионного анализа заключается в выявлении соотношения между тремя видами разнообразия: внутригрупповым, межгрупповым и общим. При этом межгрупповая (факториальная) дисперсия выявляет сумму взвешенных квадратов центральных отклонений частных средних от общей средней. Внутригрупповая (случайная) дисперсия выявляет сумму квадратов центральных отклонений признаков от частных средних. Общая дисперсия выявляет сумму квадратов центральных отклонений признаков от общей средней величины. Поэтому в любом дисперсионном комплексе имеется возможность определить силу влияния фактора на признак, рассчитав на его основе корреляционное отношение, и, наоборот, любое корреляционное отношение является отношением элементов соответствующего дисперсионного комплекса. Ранее нами было показано применение дисперсионного анализа при оценке специфики размножения, численности и распределения животных и влиянии на них как антропогенного, так и природных факторов окружающей среды [2, 4, 6, 9].
В данном случае основной задачей явилась оценка силы воздействия факторов среды на численность (хi) сообществ мелких млекопитающих (в % на 100 ловушко/суток) в трех подзонах среднего Поволжья. Количество учетных единиц по биотопам и подзонам различно, поэтому дисперсионный комплекс получился двухфакторный (подзоны и биотопы) неравномерный (разное число учетных единиц). Наиболее простой схемой расчета является анализ однофакторного равномерного дисперсионного комплекса [4]. Так как, в нашем случае, комплекс двухфакторный (три географические подзоны: А1 – южнотаежная, А2 – смешанный лес, А3 – лесостепная; и четыре биотопа: В1 – сосновый бор, В2 – смешанный лес, В3 – пойма, В4 - дубрава, представленные в каждой из них) и неравномерный (количество проб в биотопах и подзонах неодинаково), мы приводим достаточно подробный алгоритм расчета. Основная информация для расчета дисперсионного комплекса представлена в таблице 1.
Таблица 1
Схема дисперсионного анализа двухфакторного неравномерного комплекса
|
А,В х |
А1 |
А2 |
А3 |
Сумма |
|||||||||
|
В1 |
В2 |
В3 |
В4 |
В1 |
В2 |
В3 |
В4 |
В1 |
В2 |
В3 |
В4 |
||
|
хi |
3,1 - 2,2 - 2,8 - 2,4 - 3,6 |
3,1 - 5,4 - 25,2 - 28,0 - 14,7 |
5,4 - 9,2 - 4,0 - 5,0 - 4,9 |
10,2 - 8,9 - 7,9 - 12,0 - 9,6 |
5,3 - 12,9 - 14,2 - 6,2 - 4,8 - 9,1 - 5,2 - 3,9 - 2,7 - 6,6 |
18,5 - 29,8 - 28,0 - 19,2 - 11,3 - 24,0 - 9,3 - 15,5 - 14,0 - 12,5 - 10,7 - 38,0 - 21,0 - 12,7 - 21,6 |
10,9 - 8,6 - 12,5 - 14,5 - 13,2 - 12,9 - 10,6 - 16,5 - 13,6 - 14,9 |
16,5 - 14,7 - 7,3 - 8,3 - 10,5 - 14,2 - 15,8 - 10,1 - 9,9 - 12,6 |
5,3 - 6,2 - 2,9 - 3,5 - 4,4 - 5,1 - 2,8 - 5,5 - 3,6 - 4,9 |
30,1 - 14,2 - 12,8 - 9,6 - 9,5 - 10,6 - 12,4 - 13,8 - 16,4 - 10,5 - 12,3 - 10,6 - 10,7 - 12,4 - 10,9 |
32,7 - 22,5 - 20,2 - 19,9 - 28,9 - 23,4 - 19,9 - 26,6 - 28,8 - 24,5 |
10,7 - 46,5 - 57,0 - 84,5 - 57,0 - 30,0 - 20,0 - 26,7 |
а=3 b=4 |
|
n |
5 |
5 |
5 |
5 |
10 |
15 |
10 |
10 |
10 |
15 |
10 |
8 |
108 |
|
|
14 |
76 |
27 |
50 |
71 |
288 |
131 |
121 |
45 |
198 |
249 |
334 |
1604 |
|
|
3 |
15 |
5 |
10 |
7 |
19 |
13 |
12 |
5 |
13 |
25 |
42 |
169 |
|
|
8 |
231 |
29 |
100 |
50 |
369 |
172 |
146 |
20 |
174 |
620 |
1747 |
3666 |
|
|
39 |
1155 |
146 |
500 |
504 |
5530 |
1716 |
1464 |
203 |
2614 |
6200 |
13945 |
34016 |
|
|
42 |
1668 |
172 |
489 |
631 |
6464 |
1793 |
1569 |
181 |
2954 |
6424 |
18082 |
40469 |
|
|
33 |
52 |
84 |
169 |
|||||||||
|
|
68 |
169 |
441 |
678 |
|||||||||
|
|
14 |
48 |
43 |
64 |
169 |
||||||||
|
|
22 |
256 |
205 |
454 |
937 |
||||||||
На результативный признак, в данном случае численность мелких млекопитающих (хi), влияют фактор А (специфика условий существования в анализируемых подзонах), фактор В (специфика условий существования в биотопах), фактор АВ (совместное действие вышеупомянутых факторов) и фактор Z (действие прочих случайных факторов). При этом общая девиата (Dy) суммы квадратов отклонений содержит четыре компонента варьирования: Dy=DА+DВ+DАВ+Dz (а не два, как при однофакторном комплексе). Факториальная девиата (Dx) состоит из трех компонентов: Dx=DА+DВ+DАВ. В расчете дисперсионного комплекса выделяется два основных этапа.
На первом этапе находим общую девиату суммы квадратов отклонений:
![]() (1)
(1)
Затем определяем общую факториальную девиату:
![]() (2)
(2)
Далее находим остаточную девиату суммы квадратов отклонений:
![]()
![]() (3)
(3)
В этих расчетах величина (Н) определяется по формуле:
![]() (4)
(4)
Следует помнить, что если в градациях комплекса (табл. 1) разное число вариант, то n рассчитывается по формуле:
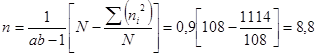 (5)
(5)
Затем переходим к выявлению числа степеней свободы:
![]()
![]()
![]()
![]()
![]() (6)
(6)
Учитывая, что комплексы неравномерные, анализ их имеет свои особенности, связанные с диспропорциональностью в распределении вариант в градациях факторов (А) и (В), что нарушает равенства Dx=DА+DВ+DАВ и DАВ=Dх-(DА+DВ), сохраняя только равенство Dy=Dx+Dz. Поэтому при обработке таких комплексов вычисляются некорректированные суммы девиат (D'x DA' DB' DAB') квадратов отклонений:
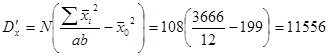 (7)
(7)
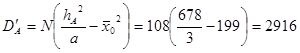 (8)
(8)
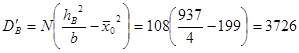 (9)
(9)
![]() (10)
(10)
В этих формулах величины ![]() и
и ![]() определяются соответственно:
определяются соответственно:
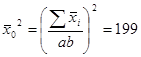
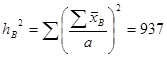 (11)
(11)
Затем находим коэффициент поправки и определяем исправленные девиаты сумм квадратов отклонений:
![]() (12)
(12)
![]()
![]()
![]()
![]() . При этом, можно проверить правильность расчетов: Dx=DА+DВ+DАВ= 2624+3353+4423=10400.
. При этом, можно проверить правильность расчетов: Dx=DА+DВ+DАВ= 2624+3353+4423=10400.
На втором этапе анализа дисперсионного комплекса рассчитываем дисперсию (s2):
![]()
![]()
![]() (13)
(13)
![]()
![]()
Затем переходим к расчету «исправленных» дисперсий (при n=8,8):
![]()
![]()
![]() (14)
(14)
![]()
![]()
После этого составляем дисперсионное отношение, т.е. фактическое воздействие факторов на численность мелких млекопитающих:
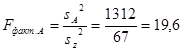
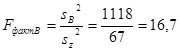
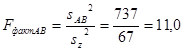 (15)
(15)
И наконец, определяем силу влияния факторов на численность мелких млекопитающих в зависимости от типов биотопов (фактор В) и природных подзон (фактор А):
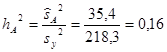
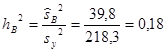
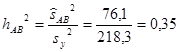 (16)
(16)
В результате проведенного исследования (табл. 2) установлено, что такой экологически значимый показатель, как численность сообществ мелких млекопитающих, определяется действием всех трех составляющих: их приуроченность к разным биотопам, разным природным подзонам и совместное влияние этих факторов. Воздействие этих факторов достаточно велико и достоверно при однопроцентном уровне значимости (табл. 2).
Показатель силы воздействия фактора А (зональность) составил 0,16, и достоверность его оказалась максимальной.
Таблица 2
Результаты дисперсионного анализа сообществ мелких млекопитающих среднего Поволжья
|
Вариация |
Степень свободы |
Девиата |
Дисперсия |
Fфакт. |
Fst. |
|
|
5% |
1% |
|||||
|
Фактор А |
2 |
2624 |
1312 |
19,6 |
3,1 |
4,8 |
|
Фактор В |
3 |
3353 |
1118 |
16,7 |
2,7 |
3,9 |
|
Совместная АВ |
6 |
4423 |
737 |
11,0 |
2,2 |
3,0 |
|
Остаточная |
96 |
6453 |
67 |
- |
- |
- |
|
Общая |
107 |
16647 |
- |
- |
- |
- |
Сила воздействия фактора В (биотопическая приуроченность) была еще выше (0,18) и также достоверна при однопроцентном уровне значимости. Максимальной силой воздействия (0,35) на численность сообществ мелких млекопитающих является совместное действие рассматриваемых факторов.
Кроме того, были рассчитаны экологические индексы, характеризующие структуру сообществ мелких млекопитающих среднего Поволжья на примере Нижегородской области (табл. 3). Максимальным биоразнообразием отличались сообщества мелких млекопитающих смешанных лесов, минимальным – лесостепной зоны. В лесных биотопах доминировала рыжая полевка, содоминантом являлась малая лесная мышь. В лугово-степных биотопах доминантом являлась обыкновенная полевка, а содоминантом – полевая мышь [3].
Таблица 3
Экологические индексы сообществ мелких млекопитающих среднего Поволжья
|
Подзона Показатели |
Природная подзона |
||
|
Южнотаежная |
Смешанный лес |
Лесостепная |
|
|
Индекс разнообразия Шеннона – Уивера |
2,217 |
2,417 |
1,793 |
|
Индекс видового богатства Маргалефа |
1,880 |
1,773 |
1,466 |
|
Индекс выровненности Пиелу |
0,840 |
0,892 |
0,748 |
|
Индекс доминирования |
0,274 |
0,220 |
0,433 |
|
Индекс полидоминантности |
3,653 |
4,554 |
2,309 |
|
Индекс разнообразия Животовского |
6,715 |
7,212 |
5,329 |
|
Индекс редких видов Животовского |
0,520 |
0,519 |
0,516 |
|
Доминант лесных сообществ |
Clethrionomys glareolus |
Clethrionomys glareolus |
Clethrionomys glareolus |
Сходство сообществ мелких млекопитающих южной тайги и лесостепи (S=0,720) конвергентное: обеднённая в видовом отношении лесостепь и заселённая в основном эвритопными видами мелких млекопитающих сходна с тайгой более чем подзоны тайги и смешанных лесов в пределах одной – лесной зоны (S=0,690). Это связано с незначительным присутствием представителей аборигенных фаун: таёжной в подзоне тайги и ещё в большей степени степной в лесостепи. Контактирующая с лесостепью подзона смешанных лесов обладает с лесостепью наибольшим сходством (S=0,769). В свою очередь подзона тайги обладает своеобразными представителями таёжного фаунистического комплекса – красной и красно-серой полёвками, а также встречалась лесная мышовка и садовая соня, подзона смешанных лесов характеризовалась наличием малой белозубки, водяной куторы, мыши-малютки, тёмной полёвки и полёвки-экономки. Кроме того, взаимодействию этих подзон препятствует такой мощный изоляционный барьер, как река Волга, что привело к наименьшему совпадению видовых спектров (S=0,690). Сходную картину дают и другие индексы общности сообществ мелких млекопитающих Нижегородской области.
Выводы
Таким образом, может быть интерпретирована и использована при экологических исследованиях сообществ позвоночных животных, составлении прогнозов численности и планировании санитарно-профилактических мероприятий в природных очагах зоонозных инфекций.