Одной из ключевых задач современной системы образования является разностороннее развитие личности обучающегося.
За годы обучения школьнику предстоит не только освоить программный материал, но и научиться способам самостоятельного приобретения знаний и приращения способностей. В связи с этим способы организации учебной деятельности обучающихся играют немаловажное значение.
На сегодняшний день проблеме формирования «универсальных учебных действий» посвящено много научных исследований и разработан целый пакет образовательных технологий. Но до сих пор многие учителя начальной школы испытывают трудности в освоении системно-деятельностного подхода.
Актуализация идей системно-деятельностного подхода обусловлена тем, что современному педагогу необходимо полностью пересмотреть алгоритм выстраивания образовательного процесса согласно новым требованиям. В первую очередь учителю требуется организовать деятельность учащихся по освоению предметных, личностных и метапредметных результатов усвоения основной образовательной программы.
Концепция развития универсальных учебных действий разработана на основе системно-деятельностного подхода, который использует предметное содержание для формирования метапредметных умений.
Понятие системно-деятельностного подхода было введено в 1985 г. как особое понятие, с помощью которого старались снять противоречие между системным подходом и деятельностным подходом, который всегда был системным. Системно-деятельностный подход является результатом объединения этих подходов [1, с.18].
Идея соединения системного и деятельностного подходов принадлежала в основном отечественным учёным и рассматривалась, в первую очередь, в трудах философов и в разных гуманитарных дисциплинах.
Первая группа ученых (Л. В. Занков, А. Г. Асмолов) рассматривает системно-деятельностный подход как метод обучения, при котором ребёнок не получает знания в готовом виде, а добывает их сам в процессе собственной учебно-познавательной деятельности.
Другие ученые считают, что системно-деятельностный подход – это такая организация учебного процесса, в которой главное место отводится активной и разносторонней, в максимальной степени самостоятельной познавательной деятельности школьника. Суть деятельностного подхода заключается в переходе от информационного репродуктивного знания к знанию действия.
Третья группа ученых (Л. С. Выготский, А. Н. Леонтьев, Д. Б. Эльконин, П. Я. Гальперин, В. В. Давыдов, Г. И. Щукина и др.) интерпретирует системно-деятельностный подход как способ организации учебно-познавательной деятельности обучаемых, при котором они являются не пассивными «приёмниками» информации, а сами активно участвуют в учебном процессе. Они считают, что деятельностный подход в обучении состоит в направлении «всех педагогических мер на организацию интенсивной, постоянно усложняющейся деятельности, ибо только через собственную деятельность человек усваивает науку и культуру, способы познания и преобразования мира, формирует и совершенствует личностные качества» [4, с.6].
В своем исследовании мы придерживаемся следующего определения системно-деятельностного подхода – это способ организации учебно-познавательной деятельности, в ходе которой у школьника происходит переход от информационно-репродуктивного знания к знанию действия.
Содержание учебного предмета выступает как система научных понятий, конституирующих определенную предметную область. В основе усвоения системы научных понятий лежит организация системы учебных действий. Как указывал В.В. Давыдов, первичная форма существования теоретического знания – это способ действия.
Именно математика занимает одну из лидирующих позиций в формировании познавательных универсальных учебных действий школьников. Ведь она способствует развитию строгого логического мышления, учит дедуктивному рассуждению, абстрагированию, умению обобщать, анализировать, критиковать. Младший школьный возраст характеризуется развитием важнейших познавательных процессов – внимания, памяти, воображения. Именно в этом возрасте данные познавательные процессы приобретают самостоятельность.
Таким образом, данные мыслительные операции могут успешно развиваться у младших школьников в результате овладения познавательными универсальными учебными действиями.
Практический опыт показывает, что особую трудность в овладении познавательными универсальными учебными действиями составляют знаково-символические действия. В частности, действие моделирование, так как оно является инструментальным базисом на уроках, позволяет упорядочить и систематизировать имеющиеся знания, вывести и конструировать новые знания.
Существует несколько подходов к определению понятия «моделирование»:
Моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическую или знаково-символическую) [5, с.30].
Моделирование в справочной литературе определяется как «метод исследования объектов и явлений при помощи их условных образов, аналогов» [6, с.15].
В педагогике выделяются два аспекта моделирования в обучении:
- Моделирование как содержание, которое учащиеся должны усвоить;
- Моделирование как учебное действие, средство обучения.
Возрастные психологические особенности младших школьников позволяют формировать универсальное учебное действие моделирование. Для математики это действие представляется наиболее важным, так как создаёт инструментарий для развития у детей познавательных универсальных действий: сравнения, классификация, анализ, и т.д., которые мы рассматривали ранее [7]. Поэтому возникает необходимость более подробно рассмотреть особенности формирования моделирования как универсального учебного действия.
Учебное моделирование – компонент содержательного анализа объекта. Несомненным достоинством учебного моделирования является то, что оно позволяет преодолеть элементы механического усвоения знаний в обучении, активизировать мыслительную деятельность учащихся. Содержание и форма моделирования зависят от того, что именно моделируется, что является предметом моделирования на конкретном этапе обучения [6, с.39].
Теория учебного моделирования берет свое начало в работах Д. Б. Давыдова и А. Ч. Варданяна, З. Д. Гольдина. Научное обоснование этой теории дано в трудах П. Я. Гальперина, которое опирается на принципы и закономерности поэтапного формирования деятельности ребенка. Такие важные положения, как требование создания полной ориентировочной основы действия, состав и последовательность этапов освоения изучаемого действия, три типа ориентировки в задании, применимы и в решении задач начального обучения. В теории планомерно-поэтапного формирования умственных действий и понятий важен каждый шаг, но один из них приобретает в нашем случае особое значение: речь идет о создании материальной и материализованной формы изучаемого действия.
Решение учебных задач, по В. В. Давыдову, представляет собой выполнение системы учебных действий (моделирование, контроль, оценка и др.), направленных на то, чтобы помочь учащимся выявить условия происхождения знаний и умений [3, с.210].
При формировании универсального учебного действия – моделирования мы опираемся на этапы, предложенные С. П. Барановым: замещение, кодирование, декодирование.
При формировании у младших школьников действия моделирования этап замещения является основополагающим, так как ребенку необходимо хорошо усвоить механизм замещения оригинала на модель с помощью знаково-символических средств. В конечном результате у учащихся получится образ-заменитель реального объекта или явления. В математике существует несколько видов таких образов-заменителей, которые можно объединить в следующие группы:
1) Заместители – точки, фигуры, цифры;
2) Знаки, которые обозначают свойства предметов.
Цвет обозначается фишкой (красной, желтой);
Форма – контур фигур (круглый, квадратный, треугольный);
Толщина – условное изображение человеческой фигуры (толстый, тонкий);
3) Символы, которые используются для замещения отношений:
равенство/неравенство (=, =);/
больше/меньше (>, <);
порядок следования (=>).
После того, как учащиеся усвоили основные образы-заменители, можно переходить ко второму этапу – кодирование.
На данном этапе осуществляется перевод текстовой, словесной информации на язык знаков, который включает два направления: графический уровень и вещественный уровень.
Результатом деятельности детей на данном этапе будет создание образа-модели оригинала с помощью знаково-символических действий.
Например, создайте образ-модель следующей информации «Шесть яблок больше, чем три яблока» на графическом и вещественном уровне.
На графическом уровне дети проиллюстрируют образ-модель таким образом: 6 > 3;
Для демонстрации на вещественном уровне детям потребуются, например, фишки, с помощью которых они кодируют данную информацию.
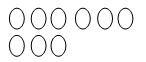
Для успешного освоения действия кодирования целесообразно использовать в педагогической деятельности разноплановые операции, которые учат детей пошаговому усвоению действий на этом этапе.
Первым шагом является преобразование модели. Данная операция включает в себя:
А) Достраивание модели
Например, при изучении геометрических фигур в 1 классе предлагаем детям достроить модель квадрата.

Основываясь на знании, что квадрат – это прямоугольник, у которого все стороны и углы равны между собой, учащиеся измеряют самую длинную сторону и достраивают фигуру до квадрата.
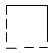
Б) Удаление лишних элементов модели
При обучении решению задачи детям предлагается исправить ошибки, допущенные в графической модели задачи: «Миша нашел 5 грибов, а дедушка – на 2 гриба больше. Сколько всего грибов нашли Миша и дедушка?»

Анализируя условие задачи, дети приходят к выводу, что модель не соответствует тексту задачи. Количество квадратов, изображенных на схеме, которые заменяют грибы, найденные Мишей, не соответствуют количеству грибов, поэтому необходимо зачеркнуть лишний.
Вторым шагом в освоении действия кодирования является работа по расшифровке модели.
При изучении площади фигуры во втором классе предлагаем детям составить все возможные равенства по модели. Таким образом, учащиеся расшифровывают графическую модель в символическую модель.

Опираясь на знания о взаимосвязи целого и части, учащиеся с помощью образов заменителей (знаков умножения, деления и равенства) расшифровывают данную модель и получают следующие равенства: 30·6=180, 6·30=180, 180:30=6, 180:6=30.
Третьим шагом является видоизменение модели.
После того, как учащиеся освоили краткую запись к задаче, предлагаем преобразовать ее в схематическую модель:

Учащиеся ложки и вилки изображают отрезками. Обобщающей скобкой обозначают вопрос задачи. Таким образом, получается следующая схема:
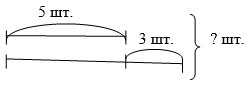
Четвертым этапом является усложнение модели:
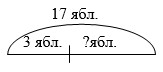
Преобразуйте схему задачи так, чтобы она соответствовала следующему выражению: (17-3)-3.
В ходе анализа схемы учащиеся приходят к выводу, что теперь необходимо найти, насколько количество яблок в первой тарелке больше, чем во второй.
Получают:
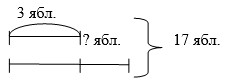
Самым сложным этапом формирования универсального учебного действия моделирования является третий этап – декодирование, так как в практике обучения он недостаточно реализуется. Декодирование – это приближение модели к оригиналу. Здесь используются следующие приемы:
А) Применение модели на практике.
При изучении площади многоугольников детям предлагается ответить на вопрос: Сколько квадратных сантиметров содержит каждая фигура?
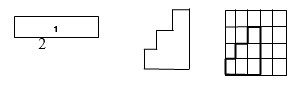
Измерив длину и ширину прямоугольника, учащиеся приходят к выводу, что площадь первой фигуры равна 5 кв. см, то есть в фигуре содержится 5 квадратов со стороной 1 см. Трудность возникает в определении площади второй фигуры, так как она представляет собой неправильный многоугольник, поэтому возникает необходимость изготовить модель квадратных сантиметров – палетку. Наложить палетку необходимо таким образом, чтобы стороны квадратов на палетке совпадали со сторонами фигуры. Далее считаем количество получившихся квадратов. Таким образом, получается, что площадь фигуры равна 6 см².
Б) Рассмотрение использования модели для описания различных предметов и явлений в реальных условиях существования (оригинала).
При изучении объемных геометрических фигур (параллелепипед, конус, пирамида, шар) учащимся предлагается задание подготовить модели геометрических фигур и с их помощью описать существенные свойства геометрических фигур. Например, аквариум – модель параллелепипеда, у него противоположные грани равны и параллельны, сигнальный конус – модель конуса, так как в основании – круг, поверхность конуса состоит из основания и боковой поверхности. Терка – модель усеченной пирамиды, так как это многогранник, основанием которого служит многоугольник, а боковыми гранями являются четырехугольники, имеющие общую сторону.
В) Соотнесение результатов, полученных в процессе моделирования, с реальностью.
Детям предлагается смоделировать три четырехугольника с площадью 12 квадратных сантиметров.
Первоначально учащимся необходимо на основе знаний о площади прямоугольника вычислить значение длины и ширины.
Таким образом, получается:

Г) Сравнение оригинала и модели как его заменителя – репрезентанта.
Учащимся предлагается выбрать текст задачи, соответствующий данной таблице:
|
|
Было |
Всего |
|
Маша |
14 шар |
? шариков |
|
Степа |
на 6 шар. больше |
- У Маши было 14 шариков, а у Степы 6 шариков. Сколько всего шариков было у детей?
- У Маши было 14 шариков, а у Степы на 6 шариков больше. Сколько всего шариков было у детей?
- У Маши было 14 шариков, а у Степы на 6 шариков больше. Сколько шариков было у Степы?
Реализация системно-деятельностного подхода на всех рассмотренных этапах системы «Оригинал – модель – оригинал» способствует эффективному формированию у младших школьников универсального учебного действия моделирования и познавательных универсальных учебных действий в целом.



