Специфика вузовского обучения приводит к тому, что студент оказывается в новых социальных и психофизиологических условиях, а часто и в новой климатической среде. К комплексу новых факторов неизбежно подключаются сложные механизмы адаптации организма. В данном случае – это сложный многоуровневый педагогический, психологический, физиологический, гигиенический и социальный комплексный процесс, определяющий здоровье и успешность обучения студентов [1]. Необходимо выявить те критические условия, которые создают психоэмоциональное перенапряжение человека, а также оптимальный режим деятельности. В этом случае необходимо использование различных математических методов исследования, которые позволяют выбрать наиболее информативный комплекс психофизиологических показателей, уменьшить случайную составляющую и оценить степень связи выделенных параметров с характеристиками жизнедеятельности человека, наметить пути повышения эффективности труда [2].
Цель работы – дать математическую оценку функционального напряжения организма студентов-медиков в процессе обучения.
Материалы и методы исследования. Объектом исследования явились студенты Карагандинского государственного медицинского университета. Всего обследовано 82 студента.
Физиологические и психометрические исследования включали: 1) измерение роста, массы тела, вычисление индексов массы тела (ИМТ) и физического состояния (ИФС); 2) определение личностной (ЛТ) и реактивной (РТ) тревожности (по методике Ч.Д. Спилбергера, Ю.Л. Ханина; 3) субъективная оценка с помощью теста САН самочувствия, активности и настроения; 4) измерение систолического (САД) и диастолического (ДАД) артериального давления, частоты пульса (ЧП), подсчет индекса Руфье – Диксона; 5) математический анализ сердечного ритма по P.M. Баевскому; 6) измерение показателей функционального состояния умственной работоспособности (корректурная таблица В.Я. Анфимова) с вычислением количества просмотренных (КПЗ) и найденных (КНЗ) знаков, число допущенных ошибок.
Статистическая обработка проводилась с помощью пакета программ Statistica 6. Для нахождения более адекватных корреляционных зависимостей были использованы интегральные уравнения, выражающие тенденции в виде полиномов третьей степени, позволяющие находить S-образные зависимости с двумя и более перегибами [3].
Доля влияния входных факторов (возраст, курс, ЛТ, ИМТ и т.д.) на физиологические показатели оценивались по методике [4]. Полученные коэффициенты парной корреляции оценивались на статистическую значимость (достоверными считались коэффициенты корреляции при Р<0.05).
Результаты и их обсуждение
Как показал анализ результатов, выявлены существенные различия в адаптации студентов к образовательной деятельности в зависимости от пола. Об этом свидетельствует вклад комплекса факторов в общую дисперсию наблюдаемых факторов (ее весомость). А поскольку, общая дисперсия есть сумма квадратов коэффициентов корреляций между аргументами (воздействующими факторами) и наблюдаемыми функциями (физиологическими показателями), это и есть своеобразная величина, определяющая весомость комплексного воздействия факторов, их значимость в формировании уровня функционального напряжения организма. У юношей общая дисперсия составляла 8,88 и девушек 14,2 усл. ед. (рисунок 1). Несмотря на выраженное отличие по вкладам комплекса факторов в общую дисперсию у юношей и девушек, существенных различий в зависимости от половой принадлежности во вкладе каждого фактора не выявлено. Так, корреляционный анализ показал (рис. 2), что основным фактором, влияющим на уровень функционального состояния организма, у студентов является индекс физического состояния, дисперсия которого составляла у юношей – 2,57 усл. ед., у девушек – 3,0 усл. ед. Следовательно, у студентов уровень функционального напряжения в процессе обучения в большей степени обусловлен физическим компонентом.
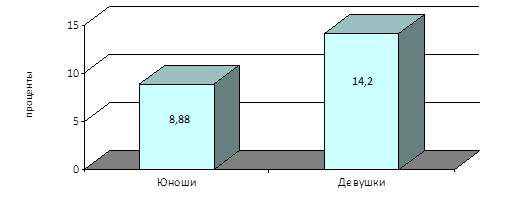
Рис.1. Показатель общей дисперсии в зависимости от пола студентов
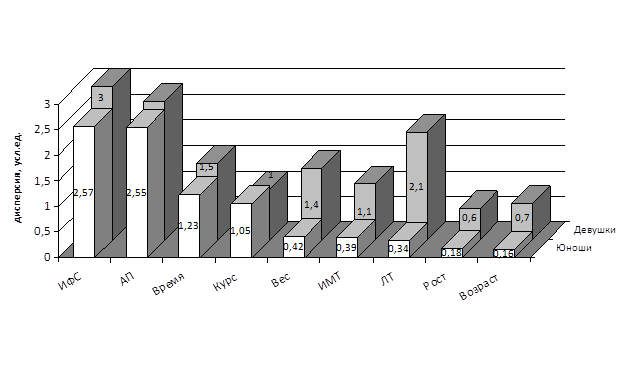
Рис. 2. Абсолютные значения дисперсии факторов и процент вклада каждого из них в общую дисперсию в зависимости от пола студентов
Вторым по значимости был фактор – адаптационный потенциал (2,55 и 2,7 усл. ед., соответственно). Это свидетельствует, что у студентов, после физического компонента, уровень функционирования организма и отдельных его систем обусловлен степенью адаптированности к среде обитания, в том числе и к образовательной среде, т.е. учебному процессу. На третьем месте выступает фактор – «время», характеризующий уровень функционирования систем организма в динамике учебного дня (1,23 и 1,5 усл. ед.). Далее шел фактор «курс», характеризующий продолжительность обучения студентов в вузе (1,05 и 1,0 усл. ед.).
У остальных факторов дисперсия была ниже единицы, вследствие чего статистическая значимость данных факторов существенно снижалась, за исключением фактора личностная тревожность (ЛТ). Здесь отмечались существенные различия во вкладе данного фактора в общую дисперсию в зависимости от половой принадлежности. Так, если у юношей дисперсия составляла 0,63 усл. ед., то у девушек она составляла 2,1 усл. ед. и выходила третьим в градации факторов по значимости их вклада. А поскольку под личностной тревожностью понимается устойчивая склонность воспринимать большой круг ситуаций (в том числе и учебный процесс) как угрожающие, то девушки выраженнее реагируют на такие ситуации состоянием тревоги, чем юноши.
В таблице 1 представлены корреляционные зависимости между воздействующими факторами (аргументами) и ответной реакцией организма в виде изменений отдельных физиологических показателей (функцией).
Таблица 1
Корреляционная зависимость между физиологическими показателями и входными факторами
|
Юноши |
ИФС |
АП |
Время |
Курс |
Вес |
ИМТ |
ЛТ |
Рост |
Воз-раст |
|
|
Юноши |
||||||||||
|
Реактивная тревожность |
0,33 |
0,49 |
0,6 |
0,31 |
0,42 |
0,31 |
||||
|
Самочувствие |
0,3 |
0,4 |
||||||||
|
Активность |
0,3 |
0,31 |
0,35 |
|||||||
|
Настроение |
0,39 |
0,43 |
||||||||
|
КПЗ |
0,29 |
0,43 |
0,33 |
0,29 |
||||||
|
КНЗ |
0,45 |
0,32 |
0,29 |
|||||||
|
Число ошибок |
0,39 |
0,39 |
0,29 |
|||||||
|
Индекс внимания |
0,29 |
0,43 |
0,33 |
0,29 |
||||||
|
САД |
0,68 |
0,87 |
||||||||
|
ДАД |
0,69 |
0,86 |
0,3 |
0,31 |
||||||
|
ЧП |
0,87 |
0,57 |
0,35 |
|||||||
|
Индекс Руфье |
0,29 |
0,38 |
0,34 |
0,29 |
||||||
|
CV |
0,28 |
|||||||||
|
AMo50 |
0,36 |
|||||||||
|
SI |
0,48 |
0,42 |
||||||||
|
PHF |
||||||||||
|
PLF |
0,29 |
0,29 |
||||||||
|
PVLF |
0,29 |
0,29 |
||||||||
|
ПАРС |
||||||||||
|
Девушки |
||||||||||
|
Реактивная тревожность |
0,37 |
0,52 |
0,41 |
0,42 |
0,58 |
|||||
|
Самочувствие |
0,28 |
0,4 |
0,53 |
0,3 |
||||||
|
Активность |
0,44 |
0,28 |
||||||||
|
Настроение |
0,28 |
0,31 |
0,42 |
0,49 |
0,4 |
|||||
|
КПЗ |
0,32 |
0,32 |
0,4 |
0,29 |
||||||
|
КНЗ |
0,35 |
0,37 |
0,43 |
0,32 |
||||||
|
Число ошибок |
||||||||||
|
Индекс внимания |
0,31 |
0,32 |
0,4 |
0,29 |
||||||
|
САД |
0,68 |
0,87 |
0,4 |
0,29 |
0,37 |
|||||
|
ДАД |
0,69 |
0,82 |
0,49 |
0,4 |
||||||
|
ЧП |
0,88 |
0,68 |
0,3 |
0,33 |
0,34 |
0,45 |
0,37 |
|||
|
Индекс Руфье |
0,54 |
0,46 |
0,28 |
0,32 |
0,51 |
|||||
|
CV |
0,38 |
|||||||||
|
AMo50 |
0,37 |
0,39 |
0,43 |
0,39 |
||||||
|
SI |
0,46 |
0,37 |
0,29 |
0,44 |
0,35 |
|||||
|
PHF |
0,36 |
0,41 |
0,29 |
0,45 |
0,5 |
0,29 |
||||
|
PLF |
0,4 |
0,31 |
0,47 |
0,39 |
0,31 |
0,33 |
0,28 |
|||
|
PVLF |
0,3 |
0,28 |
0,31 |
|||||||
|
ПАРС |
0,29 |
0,31 |
0,49 |
|||||||
|
Примечание: в таблице указаны только достоверные коэффициенты корреляции (Р<0,05); 0,38 – коэффициент линейной корреляции; 0,51 – коэффициент нелинейной корреляции (полином 3 степени). |
||||||||||
Анализ соотношения полученного числа линейных и нелинейных коэффициентов корреляций показал (рисунок 3), что высокая активность функциональных систем организма студентов в большей степени проявлялась нелинейными реакциями физиологических показателей в ответ на воздействие факторов учебного процесса, о чем свидетельствует преобладание числа нелинейных коэффициентов корреляций над линейными. Причем в количественном отношении превалировали девушки. Отмечающиеся преимущественно нелинейные зависимости свидетельствуют о менее активном прямом воздействии конкретного фактора, скорее речь идет о комбинированном и сочетанном влиянии дополнительных, сопутствующих факторов, выявление которых возможно с помощью более сложных математических методов [5].
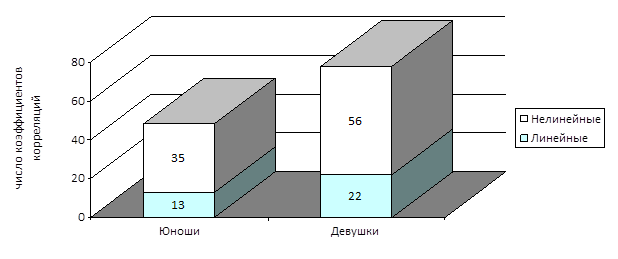
Рис. 3. Соотношение линейных и нелинейных коэффициентов корреляций у студентов
Проведенный в дальнейшем многофакторный регрессионный анализ полученных результатов физиологических исследований позволил описать выявленные корреляционные зависимости в виде уравнений регрессий.
Для юношей ведущими факторами были: коэффициент вариации полного массива кардиоинтервалов (CV), доминирующий период сверх низкочастотного компонента спектра вариабельности сердечного ритма (VLFt), мощность спектра высокочастотного компонента вариабельности в % от суммарной мощности колебаний – (HF, %), мощность спектра сверх низкочастотного компонента вариабельности в % от суммарной мощности колебаний (VLF, %). Полученное уравнения регрессии имело вид:
Y = 3.85 +0,647 * CV - 0,25 * TVLF - 0,36 * PHF - 0,67 * PVLF (1)
Оценка достоверности полученного уравнения показала высокую ее степень достоверности (коэффициент множественной корреляции = 0,836, P<0.01, критерий Фишера F =17,02, более 99,9 %).
Для девушек ведущими факторами были: коэффициент вариации полного массива кардиоинтервалов (CV), степень напряжения регуляторных систем (SI – Стресс индекс), мощность спектра высокочастотного компонента вариабельности в % от суммарной мощности колебаний (HF, %), мощность спектра низкочастотного компонента вариабельности в % от суммарной мощности колебаний (LF, %). Полученное уравнение регрессии имело вид:
Y = -10,0 + 0,533 * CV + 0,377 * SI + 0,808 * PHF + 1,22 * PLF (2)
(r= 0,811, F = 9,64, P<0.0017, более 99,9%).
В таблице 2 показаны примеры расчета значений интегрального показателя уровня функционального напряжения студентов, в процессе реальной образовательной деятельности. Подставляя значения показателей, входящих в формулу уравнения регрессии, проведя несложные арифметические операции, получаем значение расчетного показателя. Так, при использовании у девушек уравнения 2, если расчетный показатель был меньше 110 усл. ед., то уровень напряженности соответствует норме и оценивается как оптимальный, если в пределах 110–140 усл. ед. – напряжение, и если больше 140 усл. ед., то перенапряжение (неудовлетворительная). Как видно из таблицы 2, полученные количественные значения позволяют количественно оценить напряженность труда студентов в зависимости от исходных значений физиологических показателей и дать его оценку.
Таблица 2
Пример расчета уровня напряженности по уравнению 3 для девушек
|
ФИО |
CV |
SI |
PHF |
PLF |
Yрасч |
Оценка ФС |
|
Те-с Л. |
8,89 |
54,3 |
36,3 |
34,2 |
86,3 |
Норма |
|
Нед-ва Т. |
5,41 |
146,8 |
31,7 |
32,9 |
114,1 |
Напряжение |
|
Чун-ва В. |
5,69 |
246,7 |
13,2 |
67,9 |
179,6 |
Перенапряжение |
Таким образом, использование метода многофакторного корреляционно-регрессионного анализа позволило оценить влияние факторов образовательного процесса на организм студентов.
Выводы
1. Использование метода многофакторного корреляционно-регрессионного анализа позволило расчетным методом получить интегральные показатели, характеризующие уровень функционального напряжения организма студентов в процессе образовательной деятельности.
2. Проведенный линейный и нелинейный корреляционный анализ (полином 3-й степени) позволил выявить как прямые, так и S-образные корреляционные зависимости, а с помощью количественных оценок его внутренних структур выявить скрытые, объективно существующие закономерности.
3. Полученные уравнения регрессии позволяют оперативно оценить и дать прогноз уровня работоспособности студентов, как на момент обследования, так и тех или иных предполагаемых значений.



