Педагогическая теория и подходы к обучению постоянно обновляются. Это связано с необходимостью регулярного пересмотра процессов формулирования и решения задач как одной из основополагающих педагогических категорий. В данной публикации мы рассмотрим вопрос об обобщенном методе решения экспериментальных задач, являющемся частью надпредметного инструментария, согласно положениям системы согласованного обучения в контексте формирования ключевых методологических компетентностей [1].
Необходимость получения обобщённого метода связана с выявлением надпредметной его структуры соответствующего уровня обобщенности. Основными условиями полученного метода должны быть, с нашей точки зрения, независимость метода от содержания предмета и ориентированность на аудиторию различного возраста и профиля образовательного учреждения. Соблюдение неких условий, связанных с независимостью к определенным критериям или преобразованиям, принято называть термином «инвариантность». Инвариантность является одной из характеристик структуры метода.
Как известно, решение любой задачи достигается использованием частного метода. Содержание каждого частного метода составляет операционная система, через которую он реализуется. Сама система – многоуровневая и многогранная. Соответственно, можно сделать различные обобщения частных методов, получая, тем самым, методы разных уровней обобщенности, отвечающие разным признакам, которые служат критерием для определения типовых задач.
Таким образом, типовыми являются те задачи, при решении которых используется один метод (операционная система) и которые можно наименовать, используя структурные особенности метода. Число задач, входящих в один тип, определяет уровень обобщенности метода. Чем больше это число, тем метод более обобщенный.
Как правило, обобщенные методы не гарантируют ни самого решения, ни его правильности. Правильность решения гарантируют частные методы решения. Ценность обобщенных методов заключается в том, что они ориентируют действия человека, решающего задачу, поскольку в них вложена логика объекта, о котором говорится в задаче.
По отношению к выявлению структуры обобщенного метода решения экспериментальных задач, в научной литературе можно наблюдать две тенденции: непосредственное применение экспериментального метода научного исследования для решения учебных экспериментальных задач и использование экспериментальных задач для формирования творческих способностей учащихся. Поскольку познавательные процессы в научном исследовании и в обучении не идентичны, то первую тенденцию нельзя считать удачной, хотя надо учесть, что оба процесса имеют общие гносеологические закономерности. Вторая тенденция предлагает использование экспериментальных задач для формирования творческих способностей. Эта тенденция направлена больше на самостоятельное изыскание решения учащимися, чем на выявление каких-либо закономерностей самой деятельности.
Поэтому цель нашего исследования состояла в выявлении инвариантной структуры эвристического метода решения количественных экспериментальных задач. Логика, которая вложена в эту структуру, отражает особенности экспериментальной задачи как типовой в связи с методом ее решения.
Решение количественной экспериментальной задачи начинается с представления о том, что нужно измерить некоторые величины. Процесс решения при этом ведет к получению аналитического уравнения. До этого момента решение экспериментальной и теоретической задачи сходны, поэтому можно сказать, что решение экспериментальной задачи начинается с решения теоретической с экспериментальной преднамеренностью. Будем придерживаться условной классификации задач, согласно которой они делятся на теоретические и экспериментальные; считаем теоретическими те данные, для решения которых можно найти в формулировке самой задачи или в любом другом источнике, не связанном с экспериментом или измерением. То есть экспериментальные задачи требуют для их решения проведения эксперимента и получения при этом, по меньшей мере, одного данного. Такая преднамеренность состоит в том, что решение проводится не с имеющимися данными, а с теми, которые считается возможным получить в результате спроектированного в дальнейшем эксперимента.
Одним из основоположников изучения инструментария для решения теоретических задач можно считать Дьёрдя Пойа. В многочисленных последующих работах были сформированы эвристические методы, которые повышали эффективность решения таких задач. Структуры таких методов, судя по нашим поискам, получены эмпирический путем; то есть структура метода является результатом многочисленных наблюдений за действиями тех, кто решает эти задачи, включая самого исследователя. Исследования эмпирического характера следует считать весьма важными, ибо они являются основой многих успешных результатов в обучении. Для развития теории обучения полученные методы во многом являются ориентиром, но в связи с их многочисленностью затрудняют построение теории.
Считаем весьма значимыми работы кубинского психолога, специализирующегося, в частности, в области сопровождения процесса обучения А. Лабаррере, в которых он сформировал структуру метода решения теоретических задач, опираясь на три основные функции действия, выделенные Н.Ф. Талызиной: ориентировочную, исполнительную и контрольно-корректировочную (см. рис. 1) [3]. Опора на функции действия – это теоретический подход к выявлению структуры метода решения теоретических задач.
Первое, на чем следует остановиться, это на восприятии задачи. Нужно учесть, что с психологической точки зрения, «отражение мира обладает способностью идти от восприятия формы проявления действительности к пониманию сущностных особенности вещей и явлений мира» [2]. Это значит, что с самого начала процесса решения учителем должна быть обеспечена доступность к правильному и полному восприятию формулировки задачи учащимися с учетом возможностей каждого. Первые действия для понимания задачи, соответствующие ориентировочной функции, имеют место только, если возможно полное восприятие формулировки задачи.
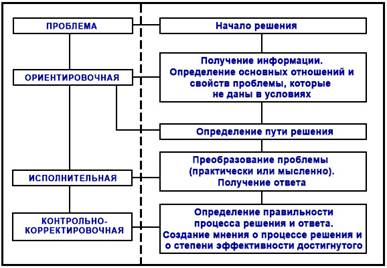
Рис. 1. Структура метода решения теоретических задач и ее соответствие с функциями действия, предложенная А. Лабаррере [5]
Проанализировав структуру рисунка 1, мы находим, что проблема – не функция действия, а форма восприятия задачи человеком, который ее решает, и начало решения – не процесс, а его начальное состояние. Поэтому, на наш взгляд, они не являются частью структуры. Еще в структуре (рис. 1) автор использует термин «ответ». Надо сказать, что ответ – форма выражения содержания конечного результата и что числовой результат – не единственный. Уравнение, имеющее в левой части величину, которую требуется найти, и в правой – величины, которые даны в условиях задачи, тоже результат. Такое уравнение представляет собой решение задачи в более общей форме, в нем содержатся все частные решения, которые удовлетворяют уравнению и сохраняют научный смысл явления, о котором толкует задача. Поэтому вместо ответа считаем более точным использовать термин «результат».
Даже поверхностный сравнительный анализ теоретической и экспериментальной задач позволяет вывести в качестве критериев для теоретического определения структуры метода решения экспериментальных задач, следующие положения:
1. Метод теоретического моделирования деятельности [3].
2. Соответствие функциям действия [6].
3. Утверждение о том, что структура метода решения теоретических задач является наименьшей структурной единицей метода решения задач, присутствующей в остальных методах решений всех других типов задач.
4. Каждая структурная составляющая метода решения задач внесет некоторый результат (промежуточный или окончательный) значимый для решения задачи.
Изучение процесса решения экспериментальных задач, основанное на отмеченных положениях, позволяет определить структуру решения экспериментальных задач (рис. 2).
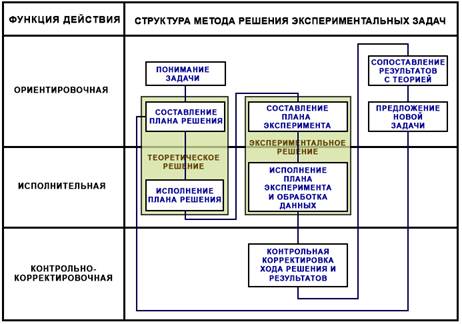
Рис. 2. Структура метода решения экспериментальных задач и ее соответствие с функциями действия (указаны теоретическое и экспериментальное решение)
Первый значимый результат для решения задачи – это ее понимание. Считается, что такой результат достигается, когда обучающийся может пересказать содержание задачи или передать информацию иными средствами. При этом не важен характер препятствия, который он должен преодолеть (языковой, знаковый и т.д.). В литературе существует ряд приемов, которыми может воспользоваться обучающийся для достижения данного результата.
Анализ рисунка 2 показывает, что при решении задачи и ориентировочная, и исполнительная функции встречаются два раза. В первый раз результатом действия ориентировочной и исполнительной функций становится аналитическое уравнение, а во второй раз, действия сфокусированы на эксперименте и ведут к конечному численному результату задачи, что позволяет нам разделить решение задачи на две части, которые, соответственно, будем называть: Теоретическое решение и Экспериментальное решение (см. рис. 2).
Несмотря на то, что этапы ориентировочной функции не следуют друг за другом, между ними существует тесная взаимосвязь. Экспериментальная преднамеренность Составления плана решения определяет некие аспекты плана эксперимента, которые на этом этапе фиксируются, чтобы получить теоретический результат (аналитическое уравнение). В свою очередь, на этапе Составления плана эксперимента завершается определение остальных аспектов эксперимента в соответствии с выбранным путем теоретического решения.
Необходимо подчеркнуть, что в процессе решения задачи субъект, выполняющей это действие, двигается нелинейно, как показано на рис. 2, а может вернуться на начальные или промежуточные этапы, особенно когда сделанные ошибки заставляют его искать новые стратегии решения.
Заметим, что в предложенной структуре есть еще два этапа, которые, как правило, не признают другие авторы: Сопоставление результатов с теорией и Предложение новой задачи. Рассмотрим их отдельно.
Можно предположить, что существование Сопоставления результатов с теорией, как этапа, связано с сопоставлением реальности и физической модели, что присуще экспериментальной задаче как таковой. Это верно и по другим причинам. Дело в том, что во многих случаях формулировка задачи представляется упрощенной ситуацией по отношению к реальности. В данной формулировке не сказано, откуда такая задача берется, почему решить ее важно в школе и в жизни. В этих случаях учащемуся непонятно, почему он такую задачу должен решить. Он допускает, что это полезно для его образования, но не находит объяснения ее пользы для жизненных или другого рода ситуаций, например, найти удельную теплоемкость сгорания этилового спирта, керосина и парафина. Такое упрощение ведет к отклонению педагогической практики от признаков познавательного процесса, а именно, к ослаблению мотивов деятельности. И это не проходит бесследно, а приводит к отсутствию этапа Сопоставления результатов с теорией при решении задач.
Следовательно, чтобы процесс обучения при решении задач соответствовал закономерности процесса познания, нужно, чтобы формулировка задачи включала ответ на вопрос: почему важно такую задачу решить, какая от нее польза, и это приведет к объективному и самопроизвольному прохождению этапа Сопоставление результатов с теорией, например:
Вы собираетесь в поход, и вам надо выбирать топливо для приготовления еды. На выбор у вас есть этиловый спирт, керосин и парафин. Решите с помощью эксперимента, что лучше взять, чтобы потратить меньше времени на приготовление еды.
На данном этапе, как правило, появляются новые вопросы по отношению к результатам решенной задачи, которые приводят к постановке самим учащимся новых задач, что и обусловливает существование этапа Предложение новой задачи. Значит, структура метода решения количественных экспериментальных задач представляется цикличной, как цепь задач, следующих одна за другой и тесно связанных друг с другом.
Процесс обучения можно построить как последовательность циклично связанных задач. Польза от такой организации процесса обучения оказывается в следующем:
1. Пониманию задачи (новой) предшествует ранее решенная задача, что подразумевает лучшее понимание новой задачи и создает лучшие возможности для Составления плана решения. В целом происходит экономия времени.
2. Поскольку постановка новой задачи возникла в результате собственных рассуждений учащихся, действия этапа могут служить повышению их мотивации.
3. Процесс решения новой задачи способствует более глубокому изучению объекта.
Детальное наблюдение за развертыванием решения экспериментальных задач позволило нам подтвердить, что ход решения происходит по указанной структуре (см. рис. 2). Однако обучающиеся поступают по-разному, применяя те или иные приемы, на которые расчленяется структура метода при решении конкретной задачи. Именно поэтому структура обобщенного метода (рис. 2) только указывает на то, что нужно получить в результате каждого этапа решения, а не дает конкретные приемы (алгоритм). Это значит, что тот, кто решает задачу, может свободно выбрать приемы, соответствующие его знаниям и опыту, то есть его собственным характеристикам.
Такая специфика хода решения задачи создает возможности для самоидентификации учащегося, что тоже является надпредметным приемом согласованного обучения, соответствующим компетентностному подходу. При возможности выбора приемов решения, измерительных инструментов и оборудования, постройки экспериментальной установки и т.д. учащийся оказывается в такой ситуации, которая дает ему возможность осознавать, какой путь познания для него эффективнее.
Нельзя сказать, что в результате исполняются все требования к самоидентификации учащегося, поскольку это происходит только в результате многочисленных и разнообразных воздействий всего обучающего процесса в целом. Поэтому важно, чтобы учитель (преподаватель) в процессе обучения выявил у учащихся признаки их собственной самоидентификации при прямом взаимодействии с ними и добился, чтобы самоидентификация стала для них осознанным действием.
Ссылаясь на то, что предложенная структура эвристического метода решения количественных экспериментальных задач самая обобщенная для такого рода деятельности, можем обозначить ее термином «макроструктура» (термин предложен Л.М. Фридманом в 1979 году [5]). Условимся называть данный метод «макроструктура решения количественных экспериментальных задач».
С позиции современного восприятия педагогической науки обучение обусловлено соответствующей целью и ориентировано на нее. Здесь сделана попытка изложить наш подход к поиску и реализации технологии обучения решению задач на обобщенном уровне в соответствии с образовательной целью – сформировать умения и навыки решения количественных экспериментальных задач на продуктивном уровне. Это значит, что в курсах физики или других естественнонаучных предметов, в которых поставлены аналогичные цели, необходимо, чтобы учащиеся освоили механизм самостоятельного решения количественных экспериментальных задач, используя макроструктуру (общий план и механизм) решения задач рассматриваемого типа.



