Данная работа является продолжением и развитием работы [7], поэтому представленные здесь результаты будут частично повторять результаты из этой работы.
Матричная модель для описания динамики численности популяций, структурированных по возрастным группам, была предложена Лесли (Leslie) в работах [9], [10]. Суть модели Лесли состоит в следующем. Пусть популяция разделена на n возрастных групп. Тогда в каждый фиксированный момент времени (например, t0) популяцию можно охарактеризовать вектор-столбцом,
![]() (t
(t![]() ) =
) =![]() ,
,
где xi(t0) – численность(t0) i-й возрастной группы (1![]() i
i![]() n). Вектор-столбец X(t1), характеризующий популяцию в следующий момент времени t1, связан с вектором X(t0) через матрицу перехода L: X(t1)=L X(t0) следующего вида
n). Вектор-столбец X(t1), характеризующий популяцию в следующий момент времени t1, связан с вектором X(t0) через матрицу перехода L: X(t1)=L X(t0) следующего вида
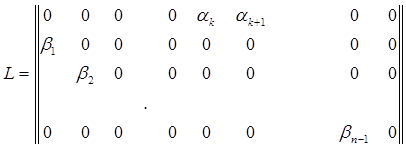 .
.
В первой строке у этой матрицы стоят коэффициенты рождаемости для i-го возраста (k≤i≤k+p), под диагональю – коэффициенты выживаемости для j-го возраста (1≤j≤n-1), а остальные элементы равны нулю.
Такой вид матрицы базируется на предположении, что за единичный промежуток времени особи j-й возрастной группы переходят в j+1-ю, при этом часть из них погибает, а у особей i-й группы рождается за этот период потомство. Тогда первая компонента вектора X(t1) будет равна
![]() ,
,
где αixi(t0) (k≤i≤k+p) – число особей, родившихся от i-й возрастной группы, а вторая и последующие – xl(t1)=βl-1xl-1(t0) (2≤l≤n, 0≤βl-1≤1), где βl-1 – коэффициент выживаемости при переходе от l-1-го возраста ко l-му.
Таким образом, зная структуру матрицы L и начальное состояние популяции – вектор-столбец X(t0), – можно прогнозировать состояние популяции в любой наперед заданный момент времени ti
X(t1)=L X(t0); X(t2)=L X(t1)= L2 X(t0); X(ti)=L X(ti-1)= Li X(t0).
Согласно теореме Перрона – Фробениуса, матрица Лесли имеет единственное положительное собственное значение λ такое, что для любого другого собственного значения r этой же матрицы выполняется условие |r|≤λ. Это собственное значение называется доминирующим, старшим или главным и характеризует скорость размножения популяции. Если все элементы матрицы являются константами, то, в зависимости от значения λ, возможен один из трех сценариев развития популяции. Если λ<1, то численность популяции будет стремиться к нулю, ecли λ>1, то будет постоянно возрастать. Наконец, если λ=1, то численность популяции, начиная с некоторого момента времени, станет постоянной, при этом соотношение между различными возрастами в ней стабилизируется. В реальности коэффициенты рождаемости и смертности могут сложным образом зависеть от общей численности популяции, соотношения ее компонент, а также от изменения условий среды обитания.
Объектом для моделирования был выбран амурский (уссурийский) тигр (Panthera tigris altacia), обитающий на юге Дальнего Востока России, а также, в Китае и, возможно, в Корее.
Начиная с 50-х годов XX века в Российской Федерации проводятся регулярные учеты численности амурских тигров, последняя из которых прошла в 2015 году. Данные этих учетов сведены в нижеследующую таблицу (по [5], [2] и [6]).
Таблица 1
Распределение и численность амурских тигров на Дальнем Востоке России
|
Год |
Приморский край |
Хабаровский край |
Всего особей |
|
1959 |
55-65 |
35 |
90-100 |
|
1965 |
70 |
- |
- |
|
1970 |
129-131 |
20 |
149-151 |
|
1976 |
- |
- |
160-170 |
|
1979 |
172-195 |
34 |
206-229 |
|
1985 |
210-220 |
- |
240-250 |
|
1990 |
338-350 |
- |
- |
|
1996 |
351-405 |
64-71 |
415-476 |
|
2005 |
357-425 |
71-77 |
428-502 |
|
2015 |
380-415 |
100-125 |
480-540 |
На основании данных учетов 1959–2005 гг., а также сведений о рождаемости и смертности в популяции, почерпнутых нами в различных источниках ([2], [4], [8]), была построена модель Лесли [7].
За единицу времени был выбран один год. Поскольку в природе продолжительность жизни амурского тигра не превышает 15 лет, то. n вектора-столбца X и матрицы L была положена равной 15. Начиная с трехлетнего возраста, самка тигра способна рожать и сохраняет эту способность до конца жизни. Раз в 2–3 года она рожает в среднем 2–3 котёнка. Считая, что плодовитость тигриц от возраста не зависит и, принимая соотношение полов в популяции равным 1:1, для коэффициентов рождаемости были установлены значения α1= α2=0, αi=0,5 (3≤i≤15).
Согласно источникам, смертность котят до 3-х лет равна примерно 50 %, что соответствует коэффициентам выживаемости β1=β2=0,71. Поскольку данных по смертности взрослых тигров в доступных источниках найти не удалось, решено было подобрать для них коэффициенты выживаемости таким образом, чтобы значения для численности популяции, полученные путем вычислений, максимально соответствовали данным учетов (на тот момент 1959–2005 гг.). Для этого с помощью программы Excel была создана матричная модель Лесли, и проведены необходимые численные эксперименты, в результате которых для коэффициентов β3=…=β14 было выбрано значение 0,815.
В итоге, матрица Лесли приобрела вид
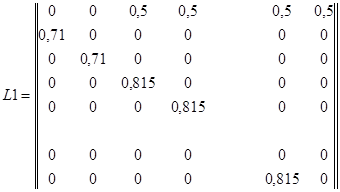 .
.
Старшее собственное число матрицы λ1=1,0387, что означает возрастание численности популяции в каждый последующий момент времени, а соответствующий ему собственный вектор V1T= (0,7011; 0,4793; 0,3276; 0,2571; 0,2017; 0,1583; 0,1242; 0,0975; 0,0765; 0,0600; 0,0471; 0,0369; 0,0290; 0,0227; 0,0178) с течением времени формирует устойчивую возрастную структуру популяции (соотношение возрастных групп внутри популяции).
Для вектор-столбца X(t0), соответствующему состоянию популяции амурского тигра в 1959 году, была выбрана структура этого собственного вектора. Общее число тигров мы положили равным 90. Полученные в результате вычислений значения численности всегда округлялись до целых чисел. Результаты вычислений представлены на приведенном ниже графике. Как можно из него видеть, применение модели Лесли для расчета динамики популяции амурского тигра дало хорошие результаты для периода с 1959 по 1996 год: полученные в результате вычислений значения либо соответствовали данным наблюдений, либо незначительно от них отличались, фиксируя увеличение численности примерно в 1,5 раза каждые 10 лет. Картина изменилась для последнего периода наблюдений. Модель дала очередное увеличение численности за 9 лет в 1,4 раза, тогда как данные обследований показали тенденцию к стабилизации численности популяции.
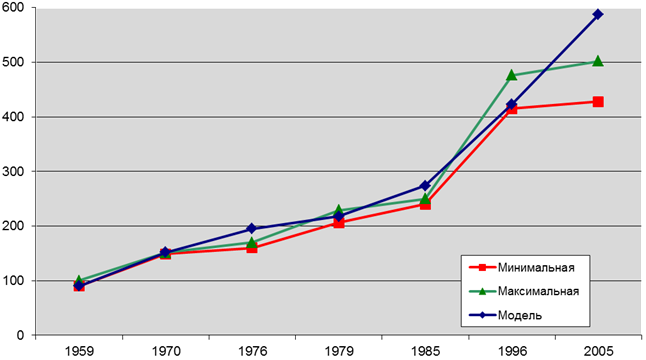
Рис.1. Оценки численности популяции амурского тигра в 1959–2005 гг. по данным учетов и c помощью одноматричной модели Лесли
Этот факт нашел следующее объяснение. За годы освоения русскими территории обитания амурского тигра, начиная с 60-х годов XIX века, происходило непрерывное уничтожение этих животных. Так продолжалось вплоть до введения запрета охоты на них в 1947 году, после чего началось постепенное восстановление численности популяции. Поскольку, по оценкам ученых, за годы интенсивной охоты первоначальная численность популяции сократилась примерно в 20 раз – с 1000 до 50 особей ([5], [3]) – увеличение её в первые десятилетия происходило в условиях избытка кормовых и пространственных ресурсов. В конце XX – начале XXI века этот процесс завершился – численность популяция достигла своего естественного предела. Почему это произошло при вдвое меньшей численности, чем в XIX веке, также находит разумное объяснение: за годы интенсивной хозяйственной деятельности человека площадь территорий, пригодных для обитания амурских тигров, значительно сократилась.
Таким образом, предложенная нами матрица Лесли L1 с постоянными коэффициентами может быть использована для моделирования динамики популяции Амурского тигра в период с 1959 (или даже с 1947) по 1996 год. Для описания динамики популяции этого животного в последующий период, в связи с изменившимися внешними условиями, необходимо построить матрицу Лесли с другими значениями коэффициентов, перейдя в результате к модифицированной двухматричной модели, аналогично тому, как это предложено в [1]. Для этого мы предположили, что, поскольку динамика численности популяции находится в фазе стабилизации, старшее собственное значение λ у описывающей ее матрицы Лесли должно быть приблизительно равно 1. Поскольку никаких данных об изменении уровня рождаемости за последние годы не было обнаружено, решено было получить искомую матрицу путем уменьшения коэффициентов выживаемости для котят β1 и β2. Коэффициенты выживаемости для старших возрастов остались неизменными. С помощью численных экспериментов были получены новые значения коэффициентов выживаемости β1=β2=0,635, а матрица Лесли приобрела вид
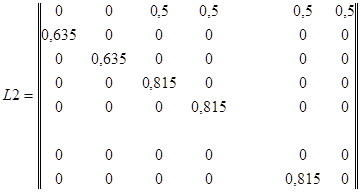 .
.
Старшее собственное число матрицы λ2=1,0021, а соответствующий ему собственный вектор V2T = (0,7302; 0,4627; 0,2932; 0,2385; 0,1939; 0,1577; 0,1283; 0,1043; 0,0849; 0,0690; 0,0561; 0,0456; 0,0371; 0,0302; 0,0246).
При моделировании динамики популяции с помощью двухматричной модели переход с матрицы L1 на матрицу L2 был осуществлен после 1999 года, когда численность достигла 475 особей. Результаты вычислений представлены на рисунке 2.
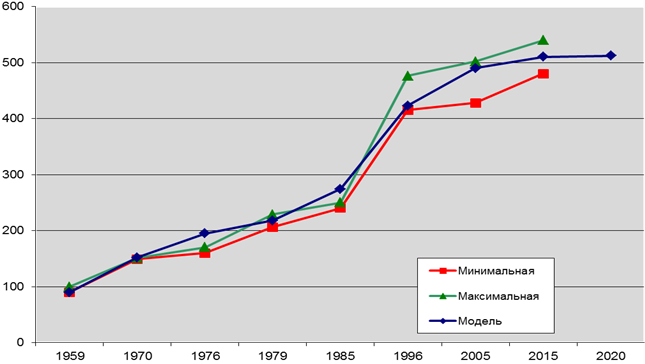
Рис. 2. Оценки численности популяции амурского тигра в 1959–2015 гг. по данным учетов и c помощью двухматричной модели Лесли
Как видно из приведенного выше графика, после 1999 года некоторое время продолжается незначительный рост численности популяции. Так, в 2015 году она составляет 510 особей, что хорошо согласуется с последними данными учетов (см. Таблицу 1). Начиная с 2017 года, согласно модели, численность популяции стабилизируется на уровне 512 особей.
Таким образом, нами была построена двухматричная модель Лесли, описывающая динамику популяции Амурского тигра на территориях Приморского и Хабаровского краев, согласующаяся с результатами учетов животного в 1959–2015 гг. Первая матрица предназначена для моделирования динамики популяции в фазе роста численности, вторая – в фазе стабилизации. Переход при моделировании с первой матрицы на вторую происходит при достижении численности популяции значения порядка 475 особей, что обусловлено ограниченным объемом кормовых и пространственных ресурсов, необходимых для существования популяции на данных территориях.
Описанная модель является достаточно грубой, что обусловлено, в первую очередь, недоступностью или отсутствием более полной информации по особенностям биологии и темпам воспроизводства вида. При ее наличии могут быть уточнены значения коэффициентов рождаемости и выживаемости, возрастная структура популяции, но общая численность популяции, рассчитываемая с помощью модели, существенно не изменится.
В заключение добавим несколько замечаний.
Во-первых, модель не описывает численность популяции на других территориях, кроме Приморского и Хабаровского краев, по причине отсутствия по ним достоверных данных. Стабилизация численности популяции на описываемых территориях не означает, что на других территориях не может происходить ее рост, как незначительный (Амурская и Еврейская Автономная области Российской Федерации), так и существенный (провинции Хэйлунцзян и Цзилинь Китайской Народной Республики).
Во-вторых, всякая популяция может переживать не только фазы роста и стабилизации, но и фазу падения численности. В нашей модели последняя фаза отсутствует, так как в современных условиях реализации межгосударственной стратегии, направленной на сохранение популяции амурского тигра, падение его численности может быть только кратковременным и обусловленным одной из следующих причин: инфекционные заболевания, резкое сокращение кормовой базы вследствие неурожая, болезней или суровой зимы, и, наконец, антропогенной катастрофы (пожар, техногенная авария). Все эти события не могут быть спрогнозированы заранее, а по их завершении популяция, скорее всего, опять окажется в фазе роста.
В-третьих, матрица L2, которая соответствует фазе стабилизации численности популяции, пригодна для моделирования именно в современных условиях и ресурсах, необходимых для существования вида. Их изменение в будущем возможно в двух направлениях, причем одновременно. В сторону уменьшения – вследствие уменьшения территорий для обитания из-за антропогенного воздействия (вырубка лесов, истребление копытных). В сторону увеличения – вследствие искусственного увеличения кормовой базы в рамках реализации программы по сохранению вида.



