Основным направлением совершенствования современного российского высшего образования в условиях его модернизации является повышение качества обучения [3, 8] и контроля знаний в рамках системного мониторинга качества этапов образовательного процесса и его результатов [2, 6, 7, 10]. Создание информационных баз данных о поэтапной системе образования, многообразие показателей мониторинговой оценки знаний предполагает использование дисперсионного анализа и позволяет делать выводы об эффективности образовательного процесса и составляющих его этапов [1, 5, 9, 10].
Цель исследования
Провести моделирование (гистограммное, среднее динамическое и трендовое) мониторинга показателей обучения студентов на примере динамики результатов первого года обучения по высшей математике студентов очной формы обучения Физико-технического института Томского политехнического университета. Оценить достоинство и недостатки предложенных 3-х моделей образовательного мониторинга на разных уровнях (институтском, направлений подготовки и групповом) в рамках дисперсионного анализа с повторными измерениями.
Материал и методы исследования
В данной работе проведен дисперсионный анализ результатов педагогических измерений знаний по высшей математике (линейная алгебра и аналитическая геометрия, дифференциальное и интегральное исчисление, дифференциальные уравнения) студентов 12-ти учебных групп очной формы обучения Физико-технического института Томского политехнического университета (выборка ФТИ объема n =144) [7] по направлениям подготовки (НП): «Физика» (Ф), «Техническая физика» (ТФ), «Прикладная математика и информатика» (ПМ), «Химическая технология материалов современной энергетики» (2 группы ХТ1 и ХТ2), «Электроника и автоматика физических установок» (2 группы ЭА1 и ЭА2) и «Ядерные физика и технологии» (5 групп ЯФ1, ЯФ2, ЯФ3, ЯФ4, ЯФ5).
Основной задачей проделанной работы являлся не одномоментный срез результатов обучения на одном из этапов учебного процесса, а прослеживание проведенных измерений от входного до рубежного контроля знаний на протяжении всего учебного года на примере одной из основных дисциплин, изучаемых студентами первого курса технического Вуза. Такой комплексный подход должен способствовать более объективной оценке полученных студентами знаний, навыков, а главное – выявлению возникающих проблем. Согласно соответствующей программе унифицированной дисциплины «Математика 1.1 и 2.1» предполагается проведение 3-х форм контроля (входного, текущего и рубежного семестрового). Для этого были использованы следующие показатели: ВИ – результаты вступительных испытаний на базе ЕГЭ (по 100 балльной шкале); ВТ – результаты входного тестирования (по 20-ти балльной шкале); АТТ1 – результаты текущей аттестации в середине 1-го семестра (по 20-30-ти балльной шкале); АТТ2 – результаты текущей аттестации в конце 1-го семестра(по 60-ти балльной шкале); ЭКЗ1 – результат классического экзамена в конце 1-го семестра (по 40-а балльной шкале) с учетом результатов ликвидации задолженностей; АТТ3 – результаты текущей аттестации в середине 2-го семестра (по 20-30-ти балльной шкале); АТТ4 – результаты текущей аттестации в конце 2-го семестра (по 60-ти балльной шкале); ЭКЗ2 – результат классического экзамена в конце 2-го семестра (по 40-а балльной шкале) с учетом результатов ликвидации задолженностей; СЕМ1 – суммарные (АТТ2+ЭКЗ1) результаты 1-го семестра (по 100 балльной шкале); СЕМ2 – суммарные (АТТ4+ЭКЗ2) результаты 2-го семестра (по 100 балльной шкале). После деления числовых результатов на соответствующий максимально возможный результат и умножения на пять все результаты были приведены к единой 5-балльной шкале. Созданная таким образом в MS Excel база данных (ФТИ) использовалась затем в пакете Statistica [4] для статистического моделирования мониторинга качества обучения студентов в рамках дисперсионного анализа с повторными измерениями.
Результаты исследования и их обсуждение
Простейшей наглядной моделью такого мониторинга является гистограммная динамика результатов основных образовательных показателей (рис.1), позволяющая оценить успеваемость студентов по категориям (троечники, хорошисты, отличники).
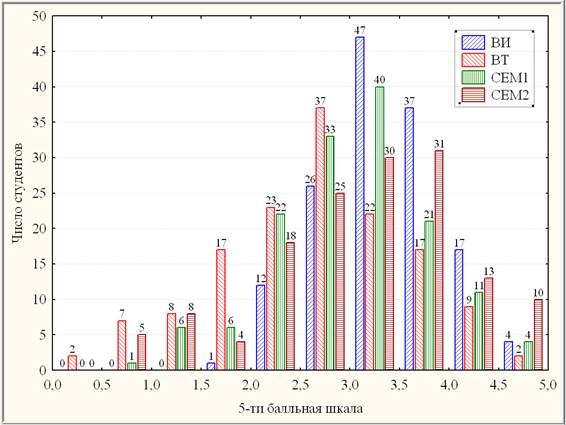
Рис. 1. Составная гистограмма ФТИ (институтская гистограммная модель)
Согласно рис. 1, наиболее контрастным является интервал сильных троечников [3; 3,5). Данная категория характеризуется сильной отрицательной динамикой входного контроля (обвал ВТ (15 %) на фоне ВИ (33 %)), положительной динамикой в 1-ом семестре (рост СЕМ1 до 28 % в сравнении с ВТ) и отрицательной динамикой во 2-ом семестре (снижение СЕМ2 до 21 % в сравнении с СЕМ1). Категория слабых хорошистов [3,5; 4) характеризуется также сильной отрицательной динамикой входного контроля (обвал ВТ (12 %) на фоне ВИ (26 %)), но дальнейшей положительной динамикой (рост СЕМ1 до 15 % в сравнении с ВТ, а затем рост СЕМ2 до 22 % в сравнении с СЕМ1). Подобная динамика характерна для категорий сильных хорошистов [4; 4,5) и отличников [4,5; 5]. Заметим, что отмеченным обвалам ВТ соответствуют доминирующие позиции ВТ в составной категории двоечников [0; 2,5).
Наряду с моделью гистограммной динамики результатов основных образовательных показателей (рис.1) возможна статистически более строгая динамическая модель числовых характеристик (параметрических и непараметрических) этих показателей, позволяющая оценить значимость их различий. При этом следует учитывать, что согласно теории измерительных шкал балльная шкала измерения образовательных показателей относится к типу порядковых шкал, позволяющих ранжировать (упорядочить) результаты оценивания качества усвоения знаний студентов. Поэтому для сравнения рассматриваемых выборок предлагается использовать прежде всего более корректные непараметрические (медианы, квартильный размах, полный размах) характеристики (рис. 2, слева), а также привычные параметрические (средние, границы доверительных интервалов) (рис. 2, справа).
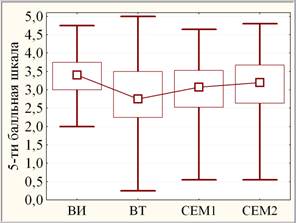
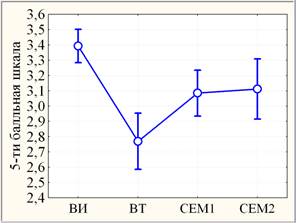
Рис. 2. Медианные диаграммы размаха (слева: квадрат – медианы; ящик – квартильный размах; усы – полный размах) и линейные графики средних (справа: круг – средние; усики – 95 % границы доверительных интервалов) ФТИ
Согласно ранговому дисперсионному анализу Фридмана с повторными измерениями динамика ФТИ (рис. 2, слева) оценивается как высоко значимая (на уровне значимости р< 0,0005) по совокупности 4-х основных образовательных показателей. При этом, согласно ранговому парному критерию Вилкоксона, ВИ отличается от ВТ высоко значимо (р< 0,0005), СЕМ1 и СЕМ2 различаются незначимо (р> 0,1), но отличаются от ВИ и ВТ сильно значимо (0,0005<р< 0,005). Данные результаты подтверждаются параметрическим дисперсионным анализом с повторными измерениями (рис. 2, справа).
Выборки СЕМ1 и СЕМ2 являются составными, что позволяет построить более детальную динамическую модель, например, параметрических числовых характеристик (рис. 3, слева) образовательных показателей ФТИ. Выборка ФТИ также является составной (6 НП), что позволяет построить еще более детальную динамическую модель параметрических числовых характеристик (рис. 3, справа) образовательных показателей НП ФТИ.
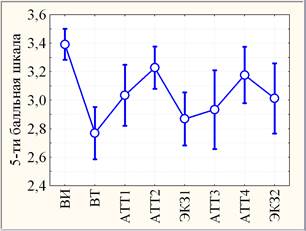
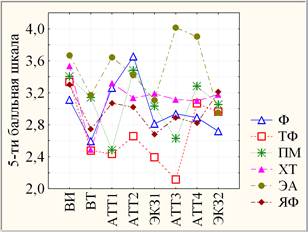
Рис. 3. Динамическая модель средних с 95 % границами доверительных интервалов образовательных показателей ФТИ (институтская – слева, на уровне НП – справа)
По параметрическому дисперсионному анализу с повторными измерениями динамика средних образовательных показателей ФТИ (рис. 3, слева) кроме уже оцененного высоко значимого (р< 0,0005) отличия ВТ от ВИ можно отметить незначимую (р> 0,1) динамику во 2-ом семестре (незначимое различие средних АТТ3, АТТ4 и ЭКЗ2), а также незначимую текущую динамику в 1-ом семестре (незначимое различие средних АТТ1 и АТТ2) при сильно значимом (0,0005<р< 0,005) отличие ЭКЗ1 от АТТ2 и статистически значимом (0,005<р< 0,05) отличие ЭКЗ1 от АТТ1. При этом АТТ1 и АТТ3 или АТТ2 и АТТ4 различаются незначимо, а ЭКЗ1 и ЭКЗ2 – статистически значимо. Заметим также, что в данном случае ЭКЗ1 незначимо отличается от ВТ и высоко значимого от ВИ, а ЭКЗ2 – статистически значимо от ВТ и – сильно значимо от ВИ. Данный анализ также позволяет выделить значимые особенности динамики средних показателей каждого НП (рис. 3, справа). Например, в случае Ф результаты ВТ отличается от ВИ слабо значимо (0,05<р< 0,10), от АТТ1 – статистически значимо, от АТТ2 – высоко значимо.
С другой стороны, в рамках однофакторного дисперсионного анализа независимых выборок с помощью параметрического F-критерия выборки показателей входного, текущего и экзаменационного контроля успеваемости оценены на однородность, то есть на различия между результатами 6-и НП (рис. 3, справа): незначимую в случае ЭКЗ2; слабо значимую – ВИ, ВТ, ЭКЗ1; статистически значимую – АТТ1, АТТ2, АТТ3, АТТ4. Данные результаты подтверждаются непараметрическим критерием Краскела – Уоллиса.
Выборка, например, ЯФ в свою очередь является составной (5 учебных групп), что позволяет построить еще более детальную динамическую модель числовых характеристик (рис. 4) образовательных показателей учебных групп НП ЯФ и их трендовую линейную модель (рис. 5).
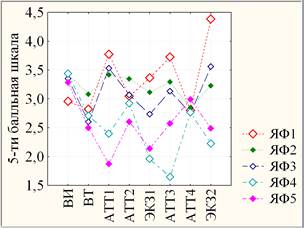
Рис. 4. Линейные графики средних образовательных показателей групп НП ЯФ (динамическая модель групповых средних)
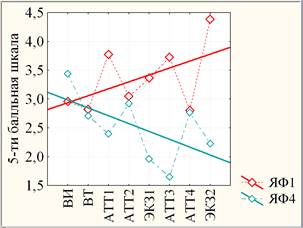
Рис. 5. Линейные тренды средних образовательных показателей групп НП ЯФ (трендовая линейная модель групповых средних)
На основании параметрического дисперсионного анализа повторных испытаний (рис. 4) можно выделить значимые особенности динамики средних показателей каждой группы НП ЯФ. Например, ЯФ1 характеризуется сильно значимой нестабильной динамикой, так что ВИ, ВТ, АТТ2, АТТ4 отличаются статистически значимо от АТТ1, АТТ3 и высоко значимо от ЭКЗ2, а ЯФ2 характеризуется слабо значимой динамикой так, что АТТ4 отличается слабо значимо от ВИ и АТТ1.
Аналогично рис. 3 (справа) в случае рис. 4 можно оценить показатели успеваемости на однородность, то есть на различия между результатами успеваемости 5-и учебных групп НП ЯФ. Согласно параметрическому F-критерию и непараметрическому критерию Краскела – Уоллиса эти различия оцениваются как незначимые в случае ВИ, ВТ, АТТ2, АТТ4 и как статистически значимые для АТТ1, ЭКЗ1, АТТ3, ЭКЗ2.
Согласно рис.5значимую нестабильную динамику средних образовательных показателей групп НП ЯФ можно наглядно характеризовать соответствующими линейными трендами, например, роста в случае ЯФ1 и спада в случае ЯФ4 с помощью уравнений линейной регрессии:
yЯФ1 = 2,82+0,120х (r = 0,52; p = 0,18) и yЯФ4 = 3,12 – 0,136х(r = -0,58; p = 0,13),
построенных по точкам (xk, yk), где xk =k – порядковый номер образовательного показателя (1-ВИ, 2-ВТ, 3-АТТ1, 4-АТТ2, 5-ЭКЗ1, 6-АТТ3, 7-АТТ4, 8-ЭКЗ2), а yk-среднее k-го образовательного показателя. В круглых скобках указаны коэффициент корреляции r и его уровень значимости p.
Результаты мониторинга ФТИ можно объяснить следующими факторами:
1) Резкое различие результатов ВТ и ВИ обусловлено несколькими причинами:
а) к ЕГЭ школьники готовятся в течение довольно длительного периода времени, структура заданий им заранее известна, происходит своего рода натаскивание именно на эти задания. В итоге результаты ЕГЭ завышены. Входное тестирование проводится в первые дни начала семестра, возможно, психологически студенты к нему не готовы, задания заранее им неизвестны;
б) задания в ЕГЭ и входном тестировании несколько отличаются. Задания в входном тестировании даются из программы школьной математики, которые нацелены на проверку именно тех знаний, которые необходимы в изучении высшей математики. И, как показывает опыт многолетнего проведения ВТ, именно этих знаний и не хватает студентам. Таким образом, можно считать, что ЕГЭ не дает объективной картины уровня знаний школьников по математике. Большой процент абитуриентов просто не готов к обучению в техническом вузе.
2) Более низкие результаты ЭКЗ по отношению к итоговой АТТ обусловлены несколькими обстоятельствами:
а) баллы аттестаций складываются из результатов контрольных работ (КР) и индивидуальных заданий (ИДЗ) по нескольким отдельным темам, а экзамен оценивает все темы семестра сразу. Многие студенты не могут сдавать большие объемы материала за весь семестр на экзамене. Большой вклад в суммарные АТТ вносят баллы за ИДЗ, которые выполняются вне аудитории в течение одной-двух недель каждое. Поэтому нельзя гарантировать, что студент выполнил ИДЗ самостоятельно;
б) большую проблему у студентов вызывают и ответы по теории на ЭКЗ, а система ЕГЭ не способствует умению думать, формулировать и доказывать теоремы, мыслить логически.
В данной работе результаты экзамена анализировались с учетом пересдач в течение нескольких недель после начала нового семестра, при первом срезе они были еще хуже. Во многих группах из-за того, что студентам приходилось пересдавать экзамен за первый семестр, очень низкими были результаты АТТ3, затем ситуация выравнивалась.
По результатам образовательного мониторинга ФТИ сформулированы предложения по повышению качества успеваемости студентов:
1) максимально приблизить условия написания КР к сдаче ЭКЗ, уменьшить вклад баллов за ИДЗ по сравнению с КР;
2) увеличить количества часов на изучение высшей математики, что помогло бы (вместе с адаптивным курсом по программе элементарной математики для слабых студентов) повысить качество знаний студентов и улучшить показатели успеваемости;
3) активно использовать электронные курсы, в том числе и на платформе Moodle, включающие в себя необходимые теоретические и практические материалы для проработки всех разделов дисциплины, а также тесты для контроля знаний. Достоинством таких электронных курсов несомненно является доступность всех материалов в любое свободное для студента время и возможность многократной проработки предлагаемых заданий.
Результаты проведенного анализа оценивания математических знаний студентов первого курса ФТИ могут быть учтены при принятии управленческих решений в организации обучения для обеспечения качества образования и контроля знаний в рамках проходящей реформы высшего образования.
Выводы:
1. Рассмотрены 3 модели мониторинга (гистограммная, динамика средних и трендовая) показателей обучения студентов по высшей математикена разных уровнях (институтском, НП и групповом).
2. Согласно дисперсионному анализу с повторными измерениями динамика образовательных показателей ФТИ оценивается как высоко значимая нестабильная на всех уровнях. При этом все независимые выборки показателей входного, текущего и экзаменационного контроля успеваемости оценены на однородность на разных уровнях.
3. На групповом уровне рассмотрена трендовая модель на основе уравнений линейной регрессии, соответствующих коэффициентов корреляции и уровней значимости отличия их от нуля.
4. По результатам образовательного мониторинга сформулированы предложения по повышению качества успеваемости студентов на основе программы адаптационного курса, а также с использованием электронных курсов.
Работа выполнена при поддержке Российского научного фонда.



