Понятие «понимание» используется в различных областях наукознания. В современной теории познания «понимание» – это метазнание, не существующее вне знания, но являющееся определённой формой знания.
Понимание рассматривается многими исследователями (Смирнов А. А, Соколов А. Н., Костюк Г. С. и др.) как опосредствованный аналитико-синтетический процесс, который включает в себя выделение «смысловых вех» и объединение их в единое целое. Понимание рассматривается как «процесс мышления, направленный на разрешение стоящих перед личностью задач. Нет оснований рассматривать понимание как какой-то особый, отдельный от мышления процесс» [5, с. 41]. Понимание подготавливается анализом, но в самый момент его возникновения оно есть всегда синтез, объединение частей в целое. Доблаев Л. П. определяет понимание как осмысление продуктов опосредствованного и обобщенного отражения связей и предлагает различать две стороны понимания: понимание как процесс и как эффект познавательных процессов [6].
Бершадский М. Е. в [1] приходит к следующим выводам: «К началу XXI в. педагогическая наука не рассматривала понимание как обязательный этап в процессе присвоения учащимися учебной информации», поскольку понимание не определено ни как педагогическая категория (не выделены существенные признаки и не определено его место в структуре учебного познания), ни как объект наблюдения (не выделена система действий учащегося, которые служат объективными индикаторами понимания ими учебной информации) [1, с. 33-34].
Брейтигам Э. К. рассматривает понимание с педагогической точки зрения как процесс, сопровождающий усвоение учебного материала обучающимися, но не совпадающий с ним. Понимание, вслед за Бершадским М. Е. и Зинченко В. П., она рассматривает как процесс и результат раскрытия, постижения основной идеи, сущности явления, события, установление взаимосвязей с уже имеющимися знаниями, включение нового содержания в смысловую сферу личности. Таким образом, понимание рассматривается как осмысление объекта познания, формирование смысла знания в процессе действия с ним, включения его в личностный опыт [2].
Мы будем рассматривать понимание как осмысление объекта познания, формирование смысла знания в процессе действия с ним. Понимание – это процесс, сопровождающий усвоение, идущий с ним параллельно.
Дифференцируя уровни усвоения учебного материала Беспалько В. П., Блум Б., Симонов В. П., Максимова В. Н. используют термин «понимание». Беспалько В. П. рассматривает «понимание» лишь как способность к восприятию (нулевой уровень усвоения); Блум Б. определяет «понимание» – как второй уровень усвоения учебного материала из шести возможных; Симонов В. П. считает, что «понимание» – это средний уровень усвоения, следующий за «запоминанием» и до «применения»; Максимова В. Н. определяет «понимание» – как третий из четырёх возможных уровней усвоения учебного материала. Каждый из перечисленных исследователей в термин «понимание» вкладывает различный смысл. Поскольку мы рассматриваем понимание как процесс, сопровождающий усвоение – нам ближе точка зрения Бершадского М. Е., который выделяет четыре уровня понимания. Считаем, что достижение обучающимся определённого уровня понимания положительно влияет на уровень усвоения обучающимся учебного материала. Рассмотрим возможные уровни понимания учебного материала.
Бершадский М. Е. выделяет четыре уровня понимания: предпонимание, генетическое понимание, структурное понимание и системное понимание. Остановимся подробнее на характеристике каждого уровня. Первый уровень – это так называемое предпонимание, готовность к восприятию определенной информации (это означает, что обучаемый уже владеет некоторой суммой понятий, которые необходимы, чтобы начать или продолжить изучение конкретной темы, и видит логические связи между разными понятиями). Отметим, что Блум Б. вкладывает в термин «понимание» характеристики данного уровня понимания.
Второй уровень – генетическое понимание, т.е. понимание процесса возникновения и развития нового знания, диагностика включает: перекодирование информации, определение типа связей между разными понятиями. Позиция Симонова В. П. в определении термина «понимание» ближе к данному уровню.
Третий уровень: структурное понимание. Понимание того, что это не просто отдельные сведения, а взаимосвязанные факты, которые объединяются в целостную структуру. Последним, четвертым по счету, можно выделить уровень систематического, или системного понимания. На этом этапе относительно изолированные системы понятий, отдельные методы, должны объединиться в общую, присущую данной науке систему.
Считаем рациональным использование четырёхуровневой дифференциации понимания Бершадского М. Е. для исследования уровней понимания студентов среднего профессионального образования, поскольку предложенные уровни:
1) позволяют анализировать понимание как процесс;
2) достаточно диагностируемы, в том числе на учебном материале по математике;
3) позволяют повысить качество овладения учебного материала.
В июне 2015 года в Рубцовском аграрно-промышленном техникуме был проведён поисковый этап эксперимента на выявление уровней понимания учебного материала по математике студентами среднего профессионального образования, в нём приняли участие студенты первого курса (количество студентов, а также специальности обучения указаны в таблице).
Контингент участников поискового эксперимента
|
Группа |
Специальность |
Количество студентов |
|
ЛП-14 |
Литейное производство чёрных и цветных металлов |
20 |
|
МСХ-14 |
Механизация сельского хозяйства |
22 |
|
ЭСХ-14 |
Электрификация сельского хозяйства |
23 |
|
МЭП-14 |
Монтаж наладка и эксплуатация электрооборудования |
20 |
|
Итого: |
95 |
Необходимым условием овладения студентами учебного материала является умение работать с задачей. С целью выявления уровней понимания у студентов среднего профессионального образования нами были подобраны задачи и разработана система вопросов к каждой из них. Система вопросов составлена так, чтобы выявить, на каком уровне понимание студентами учебного материала по математике в соответствии с уровневой дифференциацией понимания по Бершадскому М. Е.
В качестве примера приведём задачи и системы вопросов к ним:
«Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба».
1. Какие стереометрические фигуры описываются в задаче?
2. Как расположены стереометрические фигуры?
3. Какая из представленных фигур имеет больший объём?
4. Что является гранью куба?
5. Что является основанием пирамиды?
6. Какое требование в задаче?
7. Какую часть от высоты куба составляет высота пирамиды?
8. Какой многоугольник является общим для пирамиды и куба?
9. Какую часть объёма куба составляет объём призмы, основанием которой является грань куба, а высота в два раза меньше высоты куба?
10. Какую часть объёма призмы составляет объём вписанной пирамиды?
11. Во сколько раз объём пирамиды меньше объёма куба?
Часть вопросов позволяет диагностировать первый уровень понимания студентами учебного материала – предпонимание, поскольку вопросы направлены на выявление понимания студентами основных понятий и наличия связей между описываемыми понятиями – это вопрос № 1: «Какие стереометрические фигуры описываются в задаче?», и вопрос № 6: «Какое требование в задаче?» Второй блок вопросов направлен на выявление типа связи между понятиями и позволяет диагностировать генетическое понимание студентов – это вопрос № 2: «Как расположены стереометрические фигуры?», вопрос № 3: «Какая из представленных фигур имеет больший объём?», вопрос № 4: «Что является гранью куба?», и вопрос № 5: «Что является основанием пирамиды?»
Третья часть вопросов направлена на диагностирование структурного понимания, поскольку вопросы выявляют понимание студентами целостной структуры понятий и их взаимосвязей – это вопрос № 7 «Какую часть от высоты куба составляет высота пирамиды?», вопрос № 8 «Какой многоугольник является общим для пирамиды и куба?», вопрос № 9 «Какую часть объёма куба составляет объём призмы, основанием которой является грань куба, а высота в два раза меньше высоты куба?», вопрос № 10 «Какую часть объёма призмы составляет объём вписанной пирамиды?», вопрос № 11 «Во сколько раз объём пирамиды меньше объёма куба?»
Диагностирование системного понимания учебного материала студентов целесообразно с помощью анализа возможностей использования общей модели решения данной задачи или её частей при решении новых задач.
Среди предложенных студентам задач присутствовала квазипрофессиональная задача (для студентов электротехнических специальностей), вопросы к которой также направлены на выявление уровней понимания учебного материала по М. Е. Бершадскому. Приведём пример такой задачи:
«Медный шток масляного выключателя (напряжением 6-10 кВ) имеет длину 0,5 м найти диаметр сечения данного штока, если его объём ![]()
![]() ».
».
Вопросы:
1. Какую форму имеет шток масляного выключателя?
2. Какая фигура является сечением штока масляного выключателя?
3. Какие значения измерений цилиндра известны в задаче?
4. Какую величину цилиндра характеризует значение 0,5 м?
5. Какую величину цилиндра характеризует значение ![]()
![]() ?
?
6. Какое требование в задаче?
7. В каких единицах рациональнее выполнять вычисления при заданных условиях?
8. Какова формула вычисления объёма цилиндра?
9. Как найти диаметр основания цилиндра, если известна высота цилиндра и его объём?
При решении квазипрофессиональных задач диагностика предпонимания студентов выявляет не только уровень готовности к восприятию определённого рода информации, но и степень понимания студентами понятий, связанных с профессиональной деятельностью:
Вопрос № 1 «Какую форму имеет шток масляного выключателя?»;
Вопрос № 3 «Какие значения измерений цилиндра известны в задаче?»;
Вопрос № 6 «Какое требование в задаче?».
Следующие вопросы позволяют диагностировать генетическое понимание, т.к. выявляют уровень понимания учебного материала при определении типов связи между понятиями:
Вопрос № 2 «Какая фигура является сечением штока масляного выключателя?»;
Вопрос № 4 «Какую величину цилиндра характеризует значение 0,5 м?»;
Вопрос № 5 «Какую величину цилиндра характеризует значение ![]()
![]() ?»;
?»;
Вопрос № 8 «Какова формула вычисления объёма цилиндра?».
Структурное понимание выявляется в данной задаче с помощью вопросов:
Вопрос № 7 «В каких единицах рациональнее выполнять вычисления при заданных условиях?»;
Вопрос № 9 «Как найти диаметр основания цилиндра, если известна высота цилиндра и его объём?».
При ответах на вопросы студенты испытывали затруднения, задавали вопросы уточняющего характера. Следует отметить, что при первичном восприятии текста квазипрофессиональной задачи, студенты электротехнических специальностей оживлялись и с интересом приступали к ответам на вопросы по данной задаче.
На диаграмме представлены результаты диагностики понимания учебного материала по Бершадскому М. Е.:
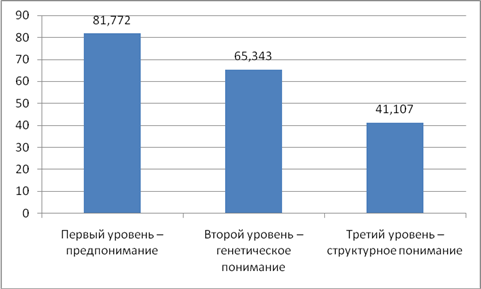
Диаграмма
В ходе проведения поискового этапа эксперимента получены следующие результаты: готовность студентов к восприятию учебной информации (предпонимание) сформировано у 81, 8 % участников эксперимента, следовательно, 18,2 % участников эксперимента не смогли дать верного ответа на вопросы, выявляющие сформированность первого уровня понимания. Возможно, у студентов возникли сложности с пониманием текста задачи и предложенных вопросов. Второй уровень понимания, который включает перекодировку информации, определение типа связей между различными понятиями (генетическое понимание) характерен для большей части опрошенных – 63,5 %. Для решения задачи необходимо понимание того, что представленные в ней данные – не отдельные сведения, а взаимосвязанные факты, объединяемые в целостную структуру (структурное понимание). Данный уровень понимания характерен для 41,1 % участников эксперимента, следовательно, 58,9 % опрошенных будут испытывать серьёзные затруднения при решении задач.
Представленные задачи и система вопросов к ним позволили выявить, для какого количества студентов (в относительных величинах от общего числа участников эксперимента) характерен первый уровень понимания (предпонимание), второй уровень понимания (генетическое понимание) и третий уровень понимания (структурное понимание). Данное исследование позволило выявить направления для дальнейшего исследования: изучить трудности, с которыми сталкиваются студенты при восприятии текста (в том числе текста задачи), исследовать возможности повышения уровня понимания студентов при использовании задач (в частности, квазипрофессиональных задач) в учебном процессе при изучении математики.



