В аналитической химии широко используются нелинейно-оптические методы диагностики материалов, основанные на различных механизмах светоиндуцированной модуляции оптических констант среды [1-3]. В этих материалах существуют концентрационные механизмы оптической нелинейности, основанные на термодиффузионном [6-7] и электрострикционном [8-9] эффектах. Светоиндуцированное изменение концентрации полимерных наночастиц приводит к соответствующей модуляции оптических свойств среды. Это позволяет реализовывать различные модификации оптического бесконтактного контроля параметров наночастиц практически в реальном времени.
Наиболее известные методы (тепловая линза, динамическая голография) успешно применяются для исследования жидких наносуспензий [3-9]. Гораздо реже используется метод псевдо-призмы, в котором в качестве измеряемого сигнала используют угол отклонения сигнального луча в слое среды с градиентом показателя преломления (метод псевдо-призмы) [10]. В частности, термоиндуцированная псевдо-призма в наносуспензии использовалась для исследования термодиффузии наночастиц [10].
В данной работе впервые предлагается использовать светоиндуцированную псевдо-призму для диагностики наногетерогенной жидкофазной среды. При этом для создания призмы в прозрачной наносуспензии используются силы светового давления.
Целью данной работы является теоретический анализ отклонения луча в светоиндуцированной псевдо-призме.
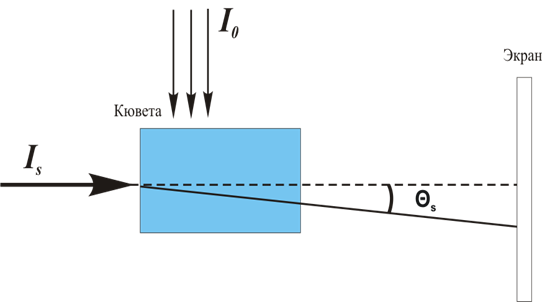
Рассмотрим жидкофазную среду с наночастицами (дисперсная фаза), находящуюся под воздействием опорного лазерного излучения с равномерным профилем интенсивности ![]() (Рис.1). Под действием сил светового давления в кювете создается градиент концентрации частиц и, соответственно, показателя преломления. Сигнальный луч
(Рис.1). Под действием сил светового давления в кювете создается градиент концентрации частиц и, соответственно, показателя преломления. Сигнальный луч ![]() распространяется перпендикулярно опорному и отклоняется в образованной псевдо-призме на угол θs.
распространяется перпендикулярно опорному и отклоняется в образованной псевдо-призме на угол θs.
|
|
|
Рис. 1. Оптическая схема псевдо-призмы. |
Для расчета угла отклонения луча в псевдо-призме используем выражение [10]:
![]() , (1)
, (1)
где ![]() -длина кюветы вдоль распространения сигнального луча,
-длина кюветы вдоль распространения сигнального луча, ![]() - показатель преломления среды.
- показатель преломления среды.
Для малой концентрации частиц с радиусом, много меньшим длины волны излучения l, показатель преломления среды пропорционален концентрации частиц [1]:
![]() , (2)
, (2)
где ![]() ;
; ![]() - показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно,
- показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно, ![]() - объемная концентрация дисперсных частиц,
- объемная концентрация дисперсных частиц, ![]() - объемная доля дисперсной среды,
- объемная доля дисперсной среды, ![]() - объем одной наночастицы.
- объем одной наночастицы.
Отсюда
![]() . (3)
. (3)
Сила светового давления, действующая на наночастицу со стороны мощного опорного луча равна[8]:
![]() , (4)
, (4)
где
 , (5)
, (5)
![]() ;
; ![]() - показатели преломления веществ дисперсионной среды и дисперсной фазы соответственно;
- показатели преломления веществ дисперсионной среды и дисперсной фазы соответственно; ![]() - радиус частицы,
- радиус частицы, ![]() - длина волны излучения,
- длина волны излучения, ![]() - скорость света.
- скорость света.
Балансное одномерное уравнение, описывающее динамику концентрации наночастиц в жидкофазной среде с учётом диффузии [8]:
![]() . (6)
. (6)
Здесь приняты следующие обозначения: ![]() - объемная концентрация дисперсных частиц, ось
- объемная концентрация дисперсных частиц, ось ![]() направлена вдоль опорного пучка
направлена вдоль опорного пучка ![]() ,
, ![]() - коэффициент диффузии. Скорость частицы
- коэффициент диффузии. Скорость частицы ![]() , где
, где ![]() - коэффициент подвижности частиц,
- коэффициент подвижности частиц, ![]() - вязкость жидкости.
- вязкость жидкости.
Соответствующие граничные условия:
![]() , при
, при ![]() и
и ![]() , (7)
, (7)
где ![]() - высота кюветы вдоль распространения опорного луча.
- высота кюветы вдоль распространения опорного луча.
Начальные условия:
![]() , при
, при ![]() , (8)
, (8)
где ![]() - начальная концентрация наночастиц.
- начальная концентрация наночастиц.
Уравнения (6)-(8) являются третьей краевой задачей нестационарного массопереноса в сплошной среде, решение которой имеет вид:
 , (9)
, (9)
где ![]() – соответствующая функция Грина:
– соответствующая функция Грина:
 , (10)
, (10)
где введены обозначения:
![]() , (11)
, (11)
 . (12)
. (12)
Здесь ![]() – корни уравнения
– корни уравнения ![]() .
.
Точное решение уравнения (3)-(5):
 (13)
(13)
Решение уравнения (10) в приближении малых изменений концентрации дает:
![]() . (14)
. (14)
Из (14) получаем для градиента концентрации наночастиц:
![]() , (15)
, (15)
Пусть зондирующий луч распространяется точно по середине кюветы. Тогда для угла отклонения такого луча получаем:
![]() . (16)
. (16)
где введены времена релаксации пространственных решеток:
![]() . (17)
. (17)
Введем безразмерный угол отклонения (нормированный на установившееся стационарное значение угла):
![]() . (18)
. (18)
Рассчитанная по формулам (16-18) зависимость угла от времени приведена на рис.2. Характерной особенностью полученной зависимости является «задержка» нелинейного отклика на малых временах.
Полученное в рамках данной модели выражение позволяет определять характеристики дисперсных наночастиц, что значительно расширяет возможности метода. Предложенная схема светоиндуцированной псевдо-призмы не требует наличия поглощения среды и поэтому свободна от обычно мешающего влияния тепловой конвекции [8-10].
Таким образом, в работе получено выражение для угла отклонения луча в светоиндуцированной псевдо-призме в прозрачной дисперсной среде (наножидкости). Полученные результаты актуальны для аналитической химии полимеров [1-5], а также для оптической диагностики дисперсных жидкофазных сред [6-10].
|
|
|
Рис. 2. Зависимость угла отклонения в псевдо-призме от времени |
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика» ФГОУ ВПО Дальневосточный государственный университет путей сообщения, г. Хабаровск;
Жуков Е.А., д.ф.-м.н., профессор, профессор кафедры "Электротехника и электроника" ФГОУ ВПО Тихоокеанский государственный университет, г. Хабаровск.