Важным фактором, влияющим на надежность эксплуатации подземных магистральных трубопроводов, является изменение геометрической формы трубопровода, то есть отклонение его положения от проектного. Всплытие и образование изгибов трубопроводов является одним из факторов, влияющих на их напряженно-деформированное состояние, которое, как известно, существенно влияет на прочностные свойства труб.
По мнению многих авторов [1, 3, 6, 8], важнейшим элементом этой проблемы является взаимодействие подземного трубопровода с окружающим грунтом. Это взаимодействие происходит как со стороны грунта за счет тепловых процессов, влажности, сил сцепления, так и со стороны трубопровода на грунт за счет действующих нагрузок, обусловленных температурой и давлением.
При строительстве трубопровода его устойчивое положение достигается за счет использования утяжелителей, в качестве средств балластировки, или непосредственного закрепления анкерами. Однако, на многих участках, особенно в северных районах, не смотря на действие утяжелителей, магистральные трубопроводы оказываются выше проектного уровня вплоть до образования вертикальных и горизонтальных изгибов.
Из анализа приведенных моделей можно выделить следующие общие закономерности. В моделях рассматривается продольное перемещение линейного участка трубопровода с низким сопротивлением грунта в перпендикулярном направлении. Такой участок можно определить, как опасный с точки зрения образования арки. Если стенка трубопровода находится в сжатом состоянии, при увеличении продольной силы (в происхождении которой модели расходятся) на рассматриваемом участке выше критического значения происходит потеря устойчивости прямолинейной формы. Значение критической силы зависит от коэффициента постели грунта и изгибной жесткости трубы [5]. Коэффициент постели резко уменьшается с увеличением обводненности грунта, что соответствует сезонному оттаиванию. Взаимодействие с грунтом может существенно ослабляться за счет вибрации.
Одновременно с обводненностью грунта возрастает выталкивающая сила, меняющая высотное положение трубы в грунте. Считается, что появление опасных участков (с низким сопротивлением и высокой обводненностью) обусловлено сложным сочетанием климатических и гидрогеологических условий, что осложняет прогнозирование аркообразования. В рассматриваемых моделях прогноз аркообразования строится на расчетах параметров опасного участка в зависимости от времени и характеристик грунта.
Таким образом, можно сделать вывод, что, не смотря на различие моделей в их прогнозной части, основанной на расчете реализации «стрелы прогиба», они достаточно хорошо предсказывают нарастание прогиба, если он уже существует.
Механизмы, обусловливающие увеличение длины линейной части трубопровода, до сих пор остаются до конца не выясненными. Так, вне рамок моделей оказывается взаимодействие трубопровода с утяжелителями. Ведь, прежде чем наступит условие реализации неустойчивости горизонтального положения трубопровода, утяжелители должны быть сброшены.
Рассмотрим стадию, предшествующую изгибу трубопровода. В качестве модели выберем стержень длиной L, закрепленный с одной стороны, и с приложенной нагрузкой F. Перемещение стержня будет определяться функцией φ(x). Кривизна стержня определяется изменением угла:
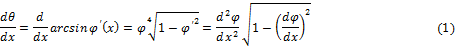
где θ – угол кривизны стержня; φ(x) – перемещение стержня.
Энергия деформации стержня будет определяться уравнением:
![]()
где E – модуль упругости; I – момент инерции сечения трубы.
Для единицы длины выберем значение массы m, тогда выражение для кинетической энергии будет иметь вид:
![]()
Потенциальная энергия изогнутого стержня определяется выражением:

где U – потенциальная энергия деформации; F – сжимающая сила.
Изгибную моду φ(x) с произвольной амплитудой можно выбрать в виде половины синусоиды:
![]()
По данным работы [2], на стадии, предшествующей моменту изгиба трубопровода, в нем должны развиваться колебания, как следствие неустойчивости:
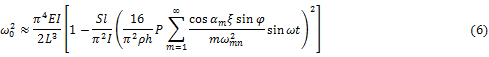
где L – длина трубы; P – давление; ρ – масса оболоки на единицу площади; h – толщина стенки; ![]() ;
x - меняющийся радиус оболочки; φ –
угол;
;
x - меняющийся радиус оболочки; φ –
угол; ![]() ,
l
- длина оболочки, m - число полуволн в направлении
образующей оболочки, n - число волн по окружности; ωmn – собственная частота колебаний.
,
l
- длина оболочки, m - число полуволн в направлении
образующей оболочки, n - число волн по окружности; ωmn – собственная частота колебаний.
Выделение частоты этих колебаний может служить основой для разработки метода мониторинга состояния трубопровода на стадии, предшествующей его изгибу. В этом случае нарушение геометрической формы будет следствием нелинейности скачков давления при неустойчивом течении газа. Уменьшение угловой частоты колебаний (1) определяет приближение системы к точке бифуркации. В задаче выделяется две траектории равновесия. В докритической области колебания (ω0) отвечают устойчивому состоянию с амплитудой (Q1).
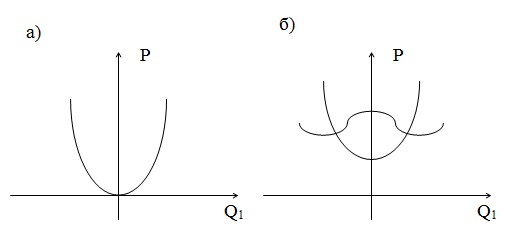
Рис. 1. Динамическое поведение трубы
а) вдали от точки бифуркации, P < Pc
б) вблизи точки бифуркации, P ≈ Pc
Управляющим параметром в этой задаче является λ = Pc – P. По мере приближения к точке бифуркации управляющий параметр убывает до нуля, вместе с ним к нулю приближается и частота собственных колебаний (ω0). В точке бифуркации потенциальная энергия видоизменяется, переходя от одноямного (устойчивого) состояния (рис. 1а) к двухямному (рис. 1б).
Появление критической нагрузки Pc соответствует исчезновению минимума потенциальной энергии. Вследствие этого частота колебаний стремится к нулю. Таким образом, обращение частоты колебаний в ноль определяет момент появления изгиба трубопровода, как переход к новому устойчивому состоянию.
Главной составляющей нагрузки (P) является продольное перемещение, вызываемое динамической нагрузкой. В работах [1, 8, 10] рассчитывается величина продольного смещения при взаимодействии с грунтом не на стадии образования изгиба, а его роста, когда изгиб уже произошел. Представляется, что и на стадии появления изгиба, взаимодействие с грунтом так же будет важным условием.
Рассмотрим появление изгибной моды при продольном нагружении трубопровода переменной динамической нагрузкой в условиях взаимодействия с грунтом. Так как грунт обладает защемляющей способностью, из всех видов взаимодействия выберем его упругое сопротивление сдвигу. Рассмотрим стационарный случай, тогда перемещение u(x) должно удовлетворять уравнению продольно-поперечного изгиба:
![]()
где D1, kn – коэффициенты, характеризующие упругие свойства грунта [9]; x – расстояние от начала участка трубопровода.
Распределение давления по длине трубопровода выберем в виде модельной функции:
![]()
Определим граничные условия:
![]()
где L – длина участка трубопровода, на котором произошел изгиб.
Уравнение (4) должно быть дополнено выражением для силы внутренних напряжений, сдавливающих трубу [1].
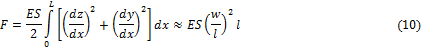
где w – величина прогиба трубопровода.
Приведенные уравнения образуют систему, решение которой определяется выражением, полученным с условиями приближения.
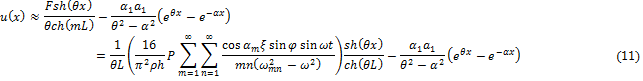
Взаимодействие с грунтом, как с упругим основанием меняет частоту моды, по которой развивается неустойчивость горизонтального положения трубопровода. Действие упругого основания поперек трубопровода может быть смоделировано пружинной подложкой, которая сопротивляется поперечным перемещениям (w). Рассмотрим линеаризованные выражения для энергии в анализе устойчивости упругого стержня. К энергии деформации изгиба

и потенциальной энергии сжимающей нагрузки

добавляется энергия деформации упругого основания

где K – жесткость основания.
Рассматривая начальную стадию закритического положения, w можно определить выражением:
![]()
где Q – амплитуда моды.
В результате проведенных преобразований можно получить выражение для ωi2 (i-я мода, по которой развивается неустойчивость):
![]()
Из этого выражения следует, что частота моды, на которой реализуется неустойчивость, оказывается больше из-за упругого взаимодействия с грунтом.
Взаимодействие трубопровода с грунтом влияет на процесс изменения его геометрической формы, то есть на отклонение от проектного положения. В работах [3, 9] показано, что на частотах от 10 Гц до 100 Гц наблюдаются максимальные амплитуды колебаний и максимальное снижение касательных сопротивлений как продольному, так и поперечному перемещению. При этом оказалось, что какой бы малой ни была амплитуда вибрации, все равно наблюдается заметное снижение упругого воздействия грунта.
Выводы:
Таким образом, динамические процессы в системе «труба-грунт» оказывают влияние на процесс удлинения линейной части трубопровода за счет роста продольных сжимающих напряжений. По мере приближения системы к моменту потери устойчивости проектного положения в ней должны происходить определенные изменения. Так, на стадии, предшествующей изгибу трубопровода, в нем развиваются низкочастотные колебания (ωi), которые затухают с ростом давления. На основании вышеизложенного, можно разработать метод прогнозирования начала появления изгиба, точнее можно
Рецензенты:
Кусков В.Н., д.т.н., профессор, ФГБОУ ВО «Тюменский государственный нефтегазовый университет», г.Тюмень;
Торопов С.Ю., д.т.н., профессор, ФГБОУ ВО «Тюменский государственный нефтегазовый университет», г.Тюмень.



