Поддержание требуемой надежности электроснабжения сложных технических систем, обеспечивающих как выполнение задач по укреплению обороноспособности страны, так и безопасности функционирования сложных технологических комплексов является актуальной научно-технической задачей. Сложность задачи поддержания требуемого уровня надежности функционирования систем электроснабжения (СЭС) обуславливается тремя особенностями, присущими только данным системам. Первое – это жесткая связь процесса производства, передачи и потребления электроэнергии. Возникновение отказа на любом этапе производства (преобразования, передачи) электроэнергии мгновенно сказывается на функционировании потребителя. Второе – скорость протекания процессов в системах электроснабжения исключает возможность включения в контур управления человека-оператора. Третья особенность – топологическая сложность построения систем электроснабжения для энергоемких объектов, обуславливаемая необходимостью обеспечения многоуровневого резервирования.
Одним из путей повышения надежности функционирования СЭС является широкое внедрение в процесс их эксплуатации средств и методов диагностирования электрооборудования (ЭО), позволяющих выявлять возникающие в нем дефекты на ранних стадиях их развития и оценивать техническое состояние оборудования в периодах между ремонтами, в том числе и без вывода его из эксплуатации. При этом возникает необходимость предварительной оценки влияния вводимых мероприятий по диагностированию ЭО на надежность функционирования системы электроснабжения в целом.
Цель исследования
Цель исследования заключается в разработке математической модели функционирования СЭС, учитывающей использование ЭО, работающего с дефектом (работоспособного) и детерминированных временных затрат на диагностирование.
Исходные предположения и допущения метода исследования
СЭС можно представить как сложную систему, состоящую из множества элементов – единиц электрооборудования, которые характеризуются набором эксплуатационных параметров Θl, которые могут изменяться. Одной из причин разброса параметров является процесс старения, который имеет, как правило, монотонный характер и обычно возрастает с течением времени или повторением возмущающих воздействий. При задании допусков на разброс параметров оборудования имеется некоторая избыточность в оценке работоспособного состояния, которая в ряде случаев может быть нерациональной. Она тем больше, чем больше у него параметров [1,2]. Может возникнуть ситуация, когда параметры оборудования находятся вне допусковой области, но внутри границ работоспособного состояния. В этом случае часто имеется возможность продолжать использовать устройство, тем самым экономя материальные и временные ресурсы.
Выделим три области значений эксплуатационных параметров и введем состояния электрооборудования:
– ЭО, исправно, если значение его параметров находится в пределах контрольной области, т.е. ![]() , где h0, hk – номинальное и контрольное значения параметра Θl соответственно, h – его величина.
, где h0, hk – номинальное и контрольное значения параметра Θl соответственно, h – его величина.
– ЭО работает с дефектом по l-му параметру (неисправно, но работоспособно), если его величина превысила контрольное значение, но находится в пределах поля допуска, установленного технической документацией, т.е. ![]() ,где hг – граница поля допуска.
,где hг – граница поля допуска.
– ЭО отказало по l-му параметру (неработоспособно), если его значение превысило границу поля допуска.
Рассмотрение промежуточного состояния между нормой и отказом необходимо при решении задачи определения возможности внедрения диагностического контроля на постоянной основе, чтобы оценить степень его влияния на надежность СЭС. Одной из важнейших характеристик процесса диагностирования является период его проведения Тд [3].
Введя состояния, в которых могут находиться электрооборудование и система электроснабжения, перейдем к построению математической модели функционирования СЭС.
Разработка модели
Реальный процесс функционирования СЭС характеризуется тем, что переход из одного состояния в другое в общем случае возможен в любой случайный момент времени. При этом выбор значения периода диагностирования Тд влияет на комплексные показатели надежности СЭС – коэффициент готовности и коэффициент технического использования. На начальном этапе определения зависимости показателей надежности от периода диагностирования необходимо построить графическую и математическую модели функционирования СЭС.
Введем понятия, отражающие степень воздействия персонала, эксплуатирующего электроустановки, на СЭС в зависимости от технического состояния электрооборудования. Процесс диагностирования ЭО состоит в том, что периодически через временной интервал Тд контролируется значение определяющего параметра, характеризующего приближение ЭО к отказу или появлению дефекта. Будем считать, что плановое диагностирование (Д) проводится при отсутствии отказа или дефекта. Если же ЭО отказало или в нем появился дефект, причем отказ и появление дефекта обнаруживаются обслуживающим персоналом, то проводится аварийный ремонт (АР) или текущий ремонт (ТР) соответственно. Следующее диагностирование назначается через период Тд после их устранения. Предполагается, что АР и ТР полностью восстанавливают ЭО.
Зададим характеристику, отражающую квалификацию обслуживающего персонала и технический уровень аппаратуры диагностирования. Обозначим через α вероятность того, что по результатам технического диагностирования не будет назначен ремонт, причем в общем случае ![]() . Если дефект при проверке не обнаруживается, то ЭО в течение времени Тд, т.е. до следующего диагностирования, рассматривается персоналом как исправное.
. Если дефект при проверке не обнаруживается, то ЭО в течение времени Тд, т.е. до следующего диагностирования, рассматривается персоналом как исправное.
Наиболее полно и целесообразно процесс функционирования СЭС описать с использованием аппарата полумарковских случайных процессов. Рассмотрим марковскую однородную стратегию обслуживания [4]. При длительной эксплуатации системы такая стратегия обслуживания вносит устойчивость, удобна при планировании работ при проведении диагностирования.
Перейдем к формальному построению модели. С учетом выделенных состояний оборудования и воздействия на нее обслуживающего персонала множество состояний S для СЭС включает следующие элементы:
- S1 – СЭС находится в состоянии исправной работы;
- S2 – ЭО диагностируется, находясь в неисправном состоянии. При обнаружении дефекта ЭО принимается решение о необходимости проведения текущего ремонта СЭС;
- S3 – СЭС отказала, проводится аварийный ремонт;
- S4 – ЭО диагностируется, находясь в исправном состоянии;
- S5 – в СЭС проводится текущий ремонт;
- S6 – СЭС работает при наличии дефекта.
Схема смены состояний СЭС приведена в виде графа, изображенного на рис. 1. На графе случайное время перехода из состояния в состояние обозначено греческой буквой t, а детерминированное – латинскими буквами t или Т.
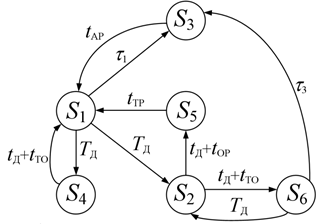
Рис.1. Ориентированный граф смены состояний СЭС в процессе его эксплуатации
В соответствии с принятыми состояниями предполагается, что заданы:
![]() – вектор функций, определяющих надежность СЭС, где F1(t) – функция распределения времени безотказной работы, F1(t) = 1-P1(t), где P1(t) – вероятность того, что за время
– вектор функций, определяющих надежность СЭС, где F1(t) – функция распределения времени безотказной работы, F1(t) = 1-P1(t), где P1(t) – вероятность того, что за время ![]() не возник отказ; F2(t) – функция распределения времени, в течение которого не возник дефект, F2(t) = 1-P2(t), где P2(t) – вероятность того, что дефект не появился за время
не возник отказ; F2(t) – функция распределения времени, в течение которого не возник дефект, F2(t) = 1-P2(t), где P2(t) – вероятность того, что дефект не появился за время ![]() ; F3(t) – функция распределения времени безотказной работы ЭО с дефектом (неисправного ЭО), F3(t) = 1-P3(t), P3(t) – вероятность того, что за время
; F3(t) – функция распределения времени безотказной работы ЭО с дефектом (неисправного ЭО), F3(t) = 1-P3(t), P3(t) – вероятность того, что за время ![]() не наступил отказ неисправного ЭО.
не наступил отказ неисправного ЭО.
А также ![]() – вектор параметров системы эксплуатации,
– вектор параметров системы эксплуатации,
где a – вероятность того, что по результатам технического диагностирования не будет назначен ремонт ЭО;
![]() – средние времена продолжительности диагностирования, технического обслуживания, ожидания ремонта, текущего и аварийного ремонтов соответственно.
– средние времена продолжительности диагностирования, технического обслуживания, ожидания ремонта, текущего и аварийного ремонтов соответственно.
Указанные предпосылки позволяют выбрать управляемый полумарковский дискретный случайный процесс ![]() [4, 5] в качестве модели функционирования СЭС, при диагностировании ЭО, где h(t) = Si означает, что в момент времени t процесс находится в состоянии Si, i = 1, 2, …, 6. На рис. 2 представлена часть одной из возможных реализаций процесса h(t).
[4, 5] в качестве модели функционирования СЭС, при диагностировании ЭО, где h(t) = Si означает, что в момент времени t процесс находится в состоянии Si, i = 1, 2, …, 6. На рис. 2 представлена часть одной из возможных реализаций процесса h(t).
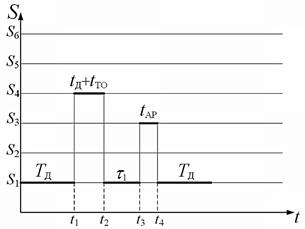
Рис.2. Пример реализации полумарковского процесса
Задача определения показателей надежности с помощью разработанной модели может быть решена через определение средней доли времени пребывания процесса h(t) в каждом из состояний Si, i = 1, 2, …, 6. Напрямую из процесса h(t) найти эти характеристики не представляется возможным, поэтому для их определения используем метод вложенных цепей Маркова [6].
Матрица переходов для цепи Маркова ![]() , соответствующая графу, изображенному на рис. 1, имеет вид:
, соответствующая графу, изображенному на рис. 1, имеет вид:
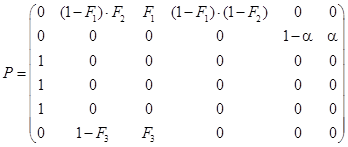 (1)
(1)
Отметим, что в (1) аргумент Тд в функциях распределений F1, F2, F3 опущен с целью упрощения записи матрицы.
Для цепи ![]() с матрицей переходных вероятностей (1) существует единственное стационарное предельное распределение вероятностей (финальные вероятности).
с матрицей переходных вероятностей (1) существует единственное стационарное предельное распределение вероятностей (финальные вероятности).
![]()
не зависящее от распределения вероятностей начального состояния, являющееся решением системы линейных уравнений:
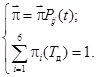 (2)
(2)
Финальные вероятности цепи Маркова для графа, описывающего функционирование СЭС, используя матрицу (1) и систему уравнений (2) в координатной форме, имеют следующий вид:
![]() (3)
(3)
где ![]()
![]() .
.
![]() , (4)
, (4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Результаты исследования и их обсуждение
Построена полумарковская модель функционирования СЭС, которая в моменты времени, соответствующие смене состояний СЭС, является однородной цепью Маркова, вложенной в процесс h(t). Модель включает в себя: ориентированный граф состояний и переходов электрооборудования, изображенный на рис. 1, матрицу вероятностных переходов (1), а также формулы вероятности переходов из состояния Si в состояние Sj, (3-8). Адекватность модели подтверждается использованием апробированного математического аппарата.
Выводы
Внедрение современных методов и средств диагностирования электрооборудования в процесс эксплуатации СЭС с целью повышения их надежности требует обоснования эффективности их использования. Разработанная математическая модель функционирования СЭС и полученные с ее помощью выражения финальных вероятностей можно использовать для определения показателей надежности систем электроснабжения, обеспечивающих как выполнение задач по обеспечению обороноспособности страны, так и безопасности функционирования сложных технологических производств.
Рецензенты:
Сеньченков В.И., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф.Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Авсюкевич Д.А., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф.Можайского» Министерства обороны РФ, г. Санкт-Петербург.



