Объект исследования – экспериментальное маломасштабное моделирование размыва дна в нижнем бьефе водосливной плотины Чебоксарской ГЭС. Предмет исследования – изучение режимов работы затворов плотины и их влияния на параметры воронки размыва. Цель работы – установление наиболее опасного режима работы затворов и режимов, при которых обеспечиваются оптимальные, с точки зрения минимизации размыва, условия движения потока в нижнем бьефе.
Подобие исследуемых процессов
Для открытых потоков, имеющих
деформируемое русло и относящихся к автомодельной области, помимо критерия
Фруда необходимо учитывать деформацию дна русла нижнего бьефа, которую в работе
определяет глубина воронки размыва, отнесенная к глубине воды в нижнем бьефе
[2, 3]. Помимо указанных динамического и геометрического параметров для оценки
влияния режима работы плотины должен быть введен параметр степени открытия
затворов плотины. Последний определяется отношением ширины водосливного
отверстия к длине водосливного фронта. Функция глубины размыва равна ![]() , где
, где ![]() –
число открытых затворов,
–
число открытых затворов, ![]() – ширина
затвора,
– ширина
затвора, ![]() – длина водосливного фронта,
– длина водосливного фронта, ![]() – число Фруда,
– число Фруда, ![]() – число затворов.
– число затворов.
В ходе экспериментального маломасштабного моделирования размыва в нижнем бьефе в качестве модельного грунта выбран однородный несвязный материал эквивалентный по механической прочности натурному. Предложена реологическая модель, в которой в качестве аналога размывающей грунт нижнего бьефа струи принят цепной рабочий орган, и использованная проф. Баловневым В.И. для анализа работы землеройных машин [1]. Составлена схема размыва дна русла в нижних бьефах гидроузлов, которая позволила определить условия однозначности геометрических, кинематических и физико-механических характеристик грунта при его взаимодействии с размывающей струей. Из условий однозначности установлена связь между масштабами параметров, характеризующих процесс размыва, что привело к определению требований к кинематическим и динамическим условиям моделирования процесса на лабораторной модели. Из полученных соотношений следует оценка взаимодействия струи с агрегатом грунта и условия перехода от связного натурного к несвязному модельному грунту [4]. Получены значения диаметра фракций модельного грунта для условий водосливной плотины Чебоксарской ГЭС. В частности, для натурных фракций связного грунта диаметром 0,1 – 0,07 мм рекомендуется модельный несвязный грунт 0,36–0,52 мм [4].
Планирование эксперимента
С целью проведения планирования эксперимента для определения глубины размыва нижнего бьефа на лабораторной установке были выделены два варьируемых фактора – степень открытия затворов плотины, определенная как отношение ширины открытых затворов к общей длине водосливного фронта, а также величина скорости в области размыва.
Для автоматизации планирования экспериментов разработана MathCAD-программа, которая на основе вводимых по результатам экспериментов данных позволила вычислить среднеарифметические значения варьируемых факторов и функции отклика, произвести линейную интерполяцию функции отклика от первого фактора и сплайн-интерполяцию функции отклика от второго варьируемого фактора. С учетом найденных минимального и максимального натурных значений факторов определены их значения в безразмерных координатах. В результате была составлена матрица ортогонального планирования и вычислены коэффициенты регрессии. На основе уравнения регрессии построены поверхность отклика и линии равного уровня данных эксперимента.
Листинг MathCAD-программы планирования эксперимента
ORIGIN:=1
Ввод данных:
-
вектор первого варьируемого фактора (опыт 1) ![]() ;
;
-
вектор второго варьируемого фактора (опыт 1) ![]() ;
;
-
вектор функции отклика (опыт 1) ![]() ;
;
-
вектор первого варьируемого фактора (опыт 2) ![]() ;
;
-
вектор второго варьируемого фактора (опыт 2) ![]() ;
;
-
вектор функции отклика (опыт 2) ![]() ;
;
-
вектор первого варьируемого фактора (опыт 3) ![]() ;
;
-
вектор второго варьируемого фактора (опыт 3) ![]() ;
;
-
вектор функции отклика (опыт 3) ![]() .
.
Среднее
арифметическое значение варьируемых факторов и функции отклика первого опыта ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Среднее
арифметическое значение варьируемых факторов и функции отклика второго опыта ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Средние
арифметические значения варьируемых факторов и функции отклика третьего опыта равны
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Для определения натуральных значений функции отклика проведена сплай-аппроксимация исходных данных эксперимента на основе составления векторов функции отклика Y от первого варьируемого фактора x1 при втором варьируемом факторе x2, используемом в качестве параметра.
Линейная интерполяция функции отклика от первого варьируемого фактора равна
![]() ,
, ![]() ,
,
![]() .
.
Сплайн-интерполяция функции отклика от второго варьируемого фактора
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Объединение
натуральных значений варьируемых факторов и функции отклика дает ![]() ,
, ![]() ,
,
![]() .
.
Ввод исходных данных ортогонального планирования двухфакторного эксперимента:
-
число варьируемых факторов ![]() ;
;
-
число опытов в полнофакторном эксперименте![]() ,
,
![]() ;
;
-
число опытов в центре плана ![]() .
.
Суммарное
число опытов ![]() ,
, ![]() .
.
Длина
«плеча» измерения фактора 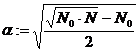 ,
, ![]() .
.
Минимальные и максимальные натуральные значения варьируемых факторов
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Натуральные значения факторов в центре плана (на основном уровне)
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Шаг
варьирования натуральных значений факторов ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Натуральные значения факторов в крайних точках «плеча» измерения фактора
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Натуральные значения функций отклика в заданных точках плана
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Переход от натуральных значений факторов к их безразмерным координатам
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Матрица ортогонального планирования
 ,
, 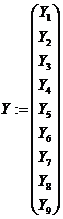 ,
,
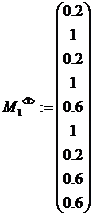 ,
,  ,
,
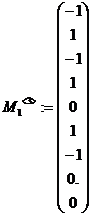 ,
, 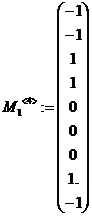 ,
,
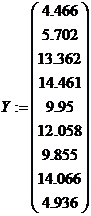 .
.
Скорректированные
значения уровней факторов для ортогонализации матрицы планирования ![]() ,
, ![]() .
.
Корректирующие координаты
![]() ,
, 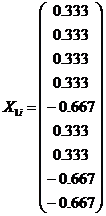 ,
,
![]() ,
, 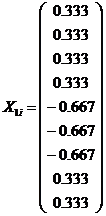 .
.
Коэффициенты регрессии
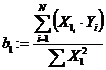 ,
, 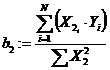 ,
,
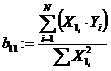 ,
, 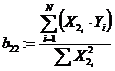 ,
,
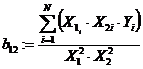 ,
, ![]() .
.
Результирующие
значения коэффициентов регрессии ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Вид
уравнения регрессии ![]() .
.
|
|
|
|
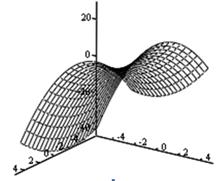
Рис. 1. Поверхность отклика на основе уравнения регрессии |
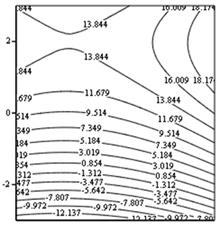
Рис. 2. Линии равного уровня на основе уравнения регрессии |
Численные значения, приведенные на линиях равного уровня (рис. 2), показывают значения глубин размыва нижнего бьефа в зависимости от степени открытия затвора и донной скорости, совпадающие с данными детальных исследований процесса размыва. Таким образом, составленная методика автоматизированных расчетов является адекватной, поскольку не противоречит результатам систематических экспериментов.
Описание модели и измерительных приборов
Для проведения экспериментального моделирования размыва в нижнем бьефе водосливной плотины Чебоксарской ГЭС была построена модель в масштабе 1:100 [3]. Лоток, отведенный под модель, обеспечивал размещение гасительной, рабочей и подпорной ее части. Ниже рисбермы модели плотины был отсеян песок крупностью 0,36…0,52 мм, образовавший согласно произведенным расчетам, размываемую часть модели [3]. Для измерения температурных эквивалентов скоростей использовались датчики-термоанемометры с аналого-цифровым преобразователем, а для измерения отметок размыва – шпиценмасштаб. Расход в лотке контролировался по мерному прямоугольному водосливу [3].
Результаты эксперимента и их обсуждение
При исследовании различных режимов работы затворов модели водосливной плотины Чебоксарской ГЭС [3] установлено, что при полном открытии одного или двух пролетов плотины образуется водоворотная зона напротив закрытых пролетов плотины, что приводит к значительным размывам дна в зоне существующей ямы. Поэтому недопустимо длительное открытие одного или двух затворов плотины полностью, если остальные пролеты закрыты. Такой режим приводит к значительным размывам за рисбермой плотины. Исследовались различные комбинации открытия пролетов плотины в режиме, когда три пролета открыты полностью, а остальные – на 6,5 м. Наиболее благоприятный гидравлический режим потока за водосливной плотиной наблюдался при полном открытии второго, четвертого и шестого затворов, а остальных на 6,5 м. Такая схема открытия является рекомендуемой. Неблагоприятный режим в нижнем бьефе и интенсификация процесса размыва наблюдались при переходе от открытия в 6,5 м к полному открытию пролетов плотины. Открытие двух пролетов плотины полностью, при условии открытия остальных четырех пролетов на 4,5 м, обеспечивает более удовлетворительный режим, но размывы грунта также имеют место. Деформации русла разной интенсивности наблюдались при всех открытиях затворов плотины, включая и полное открытие.
В
ряде случаев при обработке экспериментальных данных возникает проблема
получения функции отклика на несколько варьируемых в эксперименте переменных в
форме ![]() -мерной поверхности, где
-мерной поверхности, где ![]() – это число варьируемых факторов. При
этом данные полученные, например, для одномерного эксперимента «сшиваются» с
данными, определяющими влияние второго варьируемого фактора на ту же функцию
отклика. Указанный метод был реализован для построения функциональной
зависимости средней ширины водосбросного фронта водосливной плотины гидроузла
от глубины в нижнем бьефе при различных числах Фруда [3].
– это число варьируемых факторов. При
этом данные полученные, например, для одномерного эксперимента «сшиваются» с
данными, определяющими влияние второго варьируемого фактора на ту же функцию
отклика. Указанный метод был реализован для построения функциональной
зависимости средней ширины водосбросного фронта водосливной плотины гидроузла
от глубины в нижнем бьефе при различных числах Фруда [3].
Детальные исследования глубины воронки размыва дна отводящего русла, выполненные на русловой модели [3], показали высокую сходимость с результатами предварительного эксперимента и последующей их обработки на модели с применением предлагаемой методики «сшивки» данных.
Выводы и рекомендации
Исследование влияния режимов работы затворов водосливной плотины гидроузла, связанное с определением конечной функции отклика – глубины воронки размыва при оптимальных значениях скорости потока в нижнем бьефе водоотводящего русла, позволило установить наиболее опасные и оптимальные, минимизирующие глубину размыва, комбинации открытий пролетов.
В результате обработки данных, полученных в лабораторных экспериментах, установлено, что выбор наиболее оптимальных режимов работы затворов не приводит к остановке процесса размыва русла в нижнем бьефе. Для решения проблемы локальных размывов необходимо применение средств стабилизации руслового процесса, которые реализованы авторами виде руслоформирующих профилей на основе гибких материалов.
Рецензенты:Полянин И.А., д.т.н., профессор, профессор кафедры транспортно-технологических машин ФГБОУ ВО «Поволжский государственный технологический университет», г. Йошкар-Ола;
Царев Е.М., д.т.н., профессор, профессор кафедры технологии и оборудования лесопромышленных производств ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.