Процессу дробления массива взрывом посвящено значительное количество научных работ, однако единого мнения по данному вопросу нет.
Мосинец [3,4] предлагает рассматривать процесс дробления за счет возникновения отраженных волн и возникающих в связи с эти напряжений разрыва. Однако, установлено, что распространение трещин в процессе разрушения идет от заряда, а не наоборот.
Миндели [2] считает, что процесс разрушения горного массива взрыва связан с прохождением в нем ударных волн. Однако, установлено, что ударная волна распространяется, как правило, на ограниченном расстоянии и проходит в пределах образующейся при взрыве зоны смятия. Другим заблуждением при рассмотрении процесса дробления является представление, что нагружение массива происходит мгновенно. Однако, установлено, что на процесс разрушения оказывает влияние время действия взрывной нагрузки и скорость распространения продольных волн в массиве [1]. Тогда с учетом времени действия взрывной нагрузки (которая зависит от скорости детонации применяемого ВВ, длины заряда и места его инициирования), а также скорости распространения продольных волн за которой массив из «спокойного» состояния переходит в напряженное можно представить следующим образом:
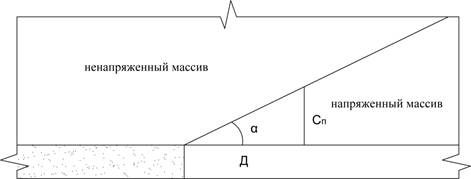
Рис. 1. Схема перехода массива в напряженное состояние
А динамическая модель разрушения массива вдоль заряда в виде (рис.2):
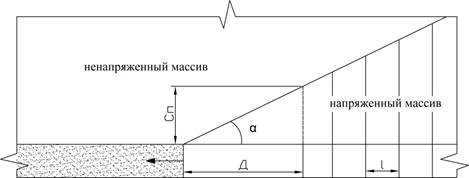
Рис. 2. Модель разрушения массива вдоль заряда
Исходя из вышеизложенного, можно представить следующие модели разрушения массива:
1. за счет изгибающего момента в массиве в виде «балки» с двумя защемленными концами (длиной l рис. 3)
2. за счет среза вдоль заряда на участках (длиной l рис. 3)
Согласно первой модели «разрушение балки с двумя защемленными концами» (с определенными допущения можно принять балку в виде трапеции).
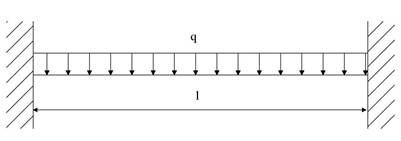
Рис.3. Схема балки с двумя защемленными концами
получим: ![]() (1)
(1)
момент сопротивления для трапеции:
![]() (2)
(2)
![]() (3)
(3)
т.е. ![]() (4)
(4)
после подстановки (преобразований?)
![]() (5)
(5)
а с учетом сопротивления с боков (работа на срез) модель можно представить следующим образом:
![]() (6)
(6)
где ![]() - равномерно распределенная нагрузка;
- равномерно распределенная нагрузка;
![]() - длина защемленной балки, м;
- длина защемленной балки, м;
![]() - расчетный радиус зоны трещин, м;
- расчетный радиус зоны трещин, м;
![]() - расчетный радиус зоны смятия, м;
- расчетный радиус зоны смятия, м;
![]() - предел прочности пород на разрыв, Мпа (
- предел прочности пород на разрыв, Мпа (![]() );
);
![]() - предел прочности пород на сжатие
- предел прочности пород на сжатие ![]() ;
;
![]() - коэффициент крепости пород по шкале Протодьяконова, д.е.;
- коэффициент крепости пород по шкале Протодьяконова, д.е.;
![]() - предел прочности пород на срез, Мпа (
- предел прочности пород на срез, Мпа (![]() ).
).
Из геометрических соображений:
![]() ;
; ![]() ;
; ![]()
где ![]() - угол раствора образующейся при взрыве воронки.
- угол раствора образующейся при взрыве воронки.
После преобразования формулы получим размер фракции вдоль заряда:
![]() (7)
(7)
где ![]() ;
;
![]() ;
;
![]()
Вторая модель разрушения за счет сдвиговых сил запишется следующим образом:
![]() ; (8)
; (8)
где ![]() - площадь боковая (
- площадь боковая (![]() );
);
![]() - площадь торцевая (
- площадь торцевая (![]() );
);
![]()
или после подстановки и преобразований получим:
![]() (9)
(9)
где ![]() - давление на контакте зона смятия - массив (
- давление на контакте зона смятия - массив (![]() ; с учетом ударного действия нагрузки
; с учетом ударного действия нагрузки ![]() ,
, ![]() ).
).
Что касается дробления массива поперек заряда, то необходимо рассматривать модель (монография), согласно которой в массиве возникают напряжения:
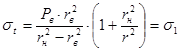 ; (10)
; (10)
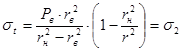 ; (11)
; (11)
Тогда согласно энергетической теории прочности получим (при ![]() ):
):
![]() ; (12)
; (12)
после подстановки и с учетом ![]() получим:
получим:
![]() (13)
(13)
где ![]() - давление продуктов детонации, Мпа;
- давление продуктов детонации, Мпа;
![]() - радиус заряда, м;
- радиус заряда, м;
![]() - радиус взрывной воронки, м.
- радиус взрывной воронки, м.
Ранее было установлено, что радиус взрывной воронки необходимо рассчитывать по предельному напряжению на срез. Однако разрушение массива внутри воронки может происходить за счет возникающих напряжений на разрыв.
С учетом размеров образующейся зоны смятия (за которой происходит дробление) получим:
![]() (14)
(14)
где 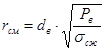 (15)
(15)
![]() - давление на контакте зона смятия - массив, МПа:
- давление на контакте зона смятия - массив, МПа: ![]()
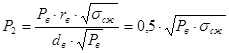
Согласно данным Г.И. Покровского [5] в массиве возникает такое число трещин, которое равно отношению максимального радиального напряжения к временному сопротивлению породы на разрыв.
Тогда, исходя из вышеизложенного, с учетом влияния зоны смятия и закономерностью 14 получим:
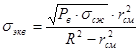 ; (16)
; (16)
а количество трещин:
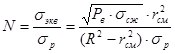 (17)
(17)
Учитывая, что для большинства пород ![]() окончательно получим (на контакте зона смятия – массив:
окончательно получим (на контакте зона смятия – массив:
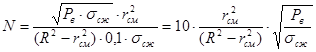 (18)
(18)
Дальнейшие изменения количества трещин в массиве можно определить из выражения 19:
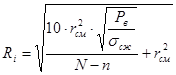 (19)
(19)
где n изменяется от 1 до (N-1);
![]() - расстояние, на котором идет изменение количества трещин в глубине массива, расположенного поперек заряда, м;
- расстояние, на котором идет изменение количества трещин в глубине массива, расположенного поперек заряда, м;
Таким образом, предполагаются модели по прогнозированию дробления массива при взрывном его нагружении цилиндрическим зарядом для различных горно-геологических и горнотехнических условий производства взрывных работ.
Рецензенты:
Косолапов А.И., д.т.н., профессор, заведующий кафедрой ОГР, Сибирский Федеральный Университет Институт горного дела, геологии и геотехнологий, г. Красноярск;
Анушенков А.Н., д.т.н., профессор, заведующий кафедрой ПРМ, Сибирский Федеральный Университет Институт горного дела, геологии и геотехнологий, г. Красноярск.



