Постановка проблемы
Флуктуации нагрузок на рабочие органы почвообрабатывающих машин имеют сложный характер, потому их невозможно моделировать детерминированными функциями времени. Адекватное представление таких нагрузок, а также колебаний, какие они возбуждают, возможно в рамках методов статистической динамики [1, 4]. Известно, что не всегда построение математической модели возможно на основе прямого физического анализа процесса, который исследуется. В таком случае необходимую информацию о поведении объекта получают по результатам экспериментального исследования в условиях нормального функционирования, когда объект находится под действием случайных возбуждений. Действующие на динамическую систему случайные возбуждения не всегда являются «белым шумом», тогда входное действие возможно представить в виде формирующего фильтра действия, который является результатом прохождения процесса типа «белого шума» через некоторую линейную систему с постоянными параметрами в виде дифференциального уравнения второго или первого порядка, в каких есть неизвестные коэффициенты корреляционной связи.
Анализ исследований
Для исследования входного действия – сопротивления почвы деформированию — в работах А.Б. Лурье [6, 7] использует твердомер динамического действия, который позволяет выполнять непрерывное определение продольной жесткости почвы, первичной информацией для возможности определения оценок вероятных характеристик которой являются осциллограммы записей изменения продольной жесткости почвы при работе агрегата в полевых условиях.
Формулировка целей статьи
Для моделирования входного действия при обработке почвы необходимо выполнить аппроксимацию корреляционной функции и спектральной плотности процесса в аналитическом виде и определить значение коэффициентов корреляционной связи.
Основная часть
Почвообрабатывающие машины с упругими подвесками рабочих органов предназначены для выполнения полезных вибраций. При решении задач оптимизации рабочих режимов таких машин необходимо учитывать случайные возбуждения, реально действующие на рабочие органы машин. В таких случаях возникают флуктуационные переходы системы из одного устойчивого периодического движения к другому периодическому движению. При этом оптимальные значения характеристик движения, соответствующие максимальной производительности, достигаются на рубеже существования заданного периодического движения.
Широко известна методика решения задач динамики линейных колебательных систем с постоянными параметрами, которые находятся под действием внешних случайных возбуждений, когда колебательные процессы выражаются в виде линейных интегральных операторов. Для нелинейных систем такой метод невозможен, поэтому придется использовать специальные методы аналитического исследования, основанные на результатах экспериментов. Аналитические решения стохастических нелинейных дифференциальных уравнений известны лишь для некоторых стохастических нелинейных дифференциальных уравнений частного вида, и их известно немного [9, 10]. Для задач, которые не имеют аналитического решения, рационально использовать метод имитационного моделирования. При моделировании входного действия возникает необходимость аппроксимации корреляционной функции сопротивления почвы аналитическим выражением, достаточным для дальнейшего исследования процесса. В работе А.Ф. Крюкова [5] доказано, что сопротивление почвы можно описать корреляционной функцией вида:
![]() , (1)
, (1)
соответствующей ей спектральной плотности:
![]() (2)
(2)
Коэффициент α характеризует интенсивность затухания корреляционной функции, а коэффициент β характеризует частоту периодической составляющей случайного процесса.
Для моделирования входного процесса необходимо определить значение коэффициентов корреляционной связи α и β. Аппроксимируя сопротивление почвы выражениями (1) и (2), значение коэффициентов корреляционной связи можно подобрать по следующим формулам:
![]() , (3)
, (3)
![]() , (4)
, (4)
где ![]() – средний период функции R(τ).
– средний период функции R(τ).
Ось τ разбивается на n отрезков ![]() между максимумами кривой R(τ). На этих отрезках определяются экстремумы кривой R(τ) и определяется логарифмический коэффициент затухания:
между максимумами кривой R(τ). На этих отрезках определяются экстремумы кривой R(τ) и определяется логарифмический коэффициент затухания:
![]() , (5)
, (5)
![]() (6)
(6)
В экспериментальном исследовании [2, 8] выполнялось непрерывное определение продольной твердости почвы. Первичной информацией для определения оценок достоверности характеристик являлись записи осциллографа по изменению продольной твердости почвы. Записи получены при работе агрегата в полевых условиях. При этом принято допущение эргодичности случайных процессов при работе агрегата, которое дает возможность в качестве первичного материала для определения корреляционной функции и спектральной плотности использовать одну осциллограмму процесса изменения твердости почвы.
Полученные корреляционные функции и спектральные плотности сопротивления почвы представлены на рисунке. Коэффициенты корреляционной связи зависят в основном от физико-механических свойств почвы и от скорости обработки почвы.
Аппроксимацией корреляционной функции и спектральной плотности реализаций сопротивления почвы определены значения коэффициентов α и β, которые представлены в таблице.
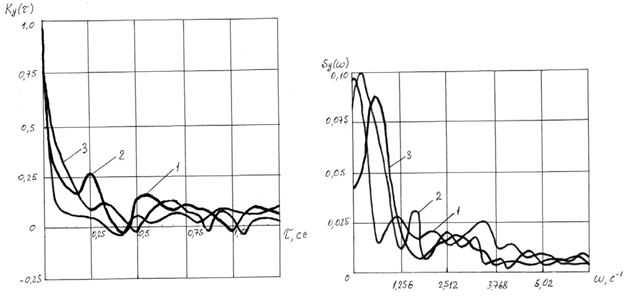
1 – V = 1,5 м/с; 2 – V = 1,78 м/с; 3 – V = 1,96 м/с
Корреляционная функция ![]() и спектральная плотность
и спектральная плотность ![]() продольной твердости почвы на скоростях движения агрегата
продольной твердости почвы на скоростях движения агрегата
Статистические оценки продольной твердости почвы
|
Статический параметр |
Обозначение |
Скорость движения, м/с |
||
|
1,96 |
1,78 |
1,6 |
||
|
Математическое ожидание |
|
2679,0 |
2358,2 |
2149,1 |
|
Среднеквадратическое отклонение |
|
51,02 |
49,1 |
45,35 |
|
Частота среза |
|
0,210 |
0,628 |
0,314 |
|
Коэффициенты корреляционной связи |
α |
0,230 |
0,290 |
0,320 |
|
β |
3,100 |
2,295 |
2,282 |
|
Выводы
Полученные в результате исследования коэффициенты корреляционной связи дают возможность выбирать дифференциальное уравнение входного действия для почвообрабатывающих машин при моделировании динамики взаимодействия рабочего органа с почвой [3]. Приведенную методику можно использовать при моделировании рабочих процессов различных почвообрабатывающих машин.
Рецензенты:
Афоничев Д.Н., д.т.н., заведующий кафедрой электротехники и автоматики, профессор Воронежского государственного аграрного университета императора Петра I, г. Воронеж;
Попиков П.И., д.т.н., профессор кафедры механизации лесного хозяйства Воронежской государственной лесотехнической академии, г. Воронеж.



