Согласно Концепции развития математического образования в Российской Федерации, математическое образование должно, с одной стороны, предоставлять каждому обучающемуся возможность достижения уровня математических знаний, необходимого для дальнейшей успешной жизни в обществе, с другой – обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др. [6]. О качестве математической подготовки школьников в той или иной мере, судят по результатам итоговой государственной аттестации. Для улучшения результатов Единого государственного экзамена (ЕГЭ) профильного уровня целесообразно проводить детальный анализ решений учащимися всех задач с развернутым ответом с целью прогнозирования путей предупреждения типичных ошибок, планирования корректирующих действий [1]. В настоящей статье проведем такой анализ на примере решений задачи 16 участниками ЕГЭ профильного уровня в Алтайском крае в 2015 году.
Стереометрическая задача 16 (ранее задача С2) относится к повышенному уровню. По сравнению с предыдущим годом в 2015 году эта задача не меняла тематику, которая заявлена как «Прямые и плоскости в пространстве. Многогранники. Тела и поверхности вращения. Измерение геометрических величин. Координаты и векторы» [3, 4, 5]. Однако произошли существенные изменения в модели задачи: она стала содержать два пункта (а и б) с требованиями «доказать» и «найти». Каждый из пунктов независимо оценивался экспертами ЕГЭ одним баллом. Соответственно:
– 2 баллами оценивалось обоснованное решение обоих пунктов;
– 1 баллом оценивалось обоснованное решение только одного из пунктов;
– 0 баллом оценивались все остальные решения [2].
В целом, в 2015 году задача 16 предполагала:
– владение как стереометрическими понятиями (такими как пирамида, высота пирамиды, перпендикулярность прямой и плоскости, угол между прямой и плоскостью и др.) так и планиметрическими (в частности, понятием прямоугольного треугольника, определениями тригонометрических функций острого угла прямоугольного треугольника и др.), а также фактами, связанными с этими понятиями;
– умение изображать пирамиду, проводить дополнительные построения, направленные на изображение и поиск угла между прямой и плоскостью;
– знание признаков перпендикулярности прямой и плоскости и умение их использовать при решении задачи;
– знание обратной теоремы Пифагора и умение ею воспользоваться в нужной ситуации;
– владение навыками нахождения угла по значению тригонометрической функции при выполнении вычислительной составляющей решения.
Приведем один из примеров задачи 16:
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 3 и BC = 4. Длины боковых ребер пирамиды ![]() ,
, ![]() и
и ![]() .
.
а) Докажите, что SA – высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
На рисунке 1 наглядно представлены результаты решения задачи 16 экзаменационной работы ЕГЭ профильного уровня учащимися Алтайского края в 2015 года в первичных баллах.
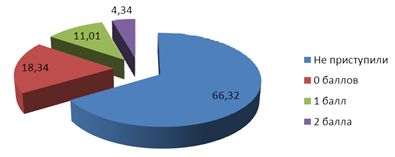
Рис. 1. Результаты решения задачи 16 в первичных баллах
Как видно из рисунка, в Алтайском крае за решение задачи 16 положительный балл (1 или 2) получили 15,35%, что находится в норме (10-50%). Однако, можно выделить ряд типичных ошибок участников экзамена при выполнении данного задания.
Типичные ошибки в решениях задачи 16
1. Самой распространенной ошибкой при решении задачи 16 в 2015 году была неверная трактовка, непонимание признака перпендикулярности прямой и плоскости: учащиеся (упрощая себе задачу) считали достаточным доказать перпендикулярность рассматриваемой прямой только одной прямой плоскости для того, чтобы утверждать перпендикулярность этой прямой и плоскости. В то время как признак гласит «Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости». В итоге доказательство в пункте а) было неверным и оценивалось 0 баллов.
Приведем типовой пример. На рисунке 2 приведено решение участника ЕГЭ, в котором рассмотрен треугольник SAD и присутствует доказательство его прямоугольности с помощью обратной теоремы Пифагора. Это дает основание утверждать только перпендикулярность прямой SA и AD, чего недостаточно для заключения перпендикулярности прямой SA и плоскости ABC, а, следовательно, не дает учащемуся права утверждать, что SA – высота пирамиды. Для верного решения учащемуся необходимо было провести аналогичные рассуждения для треугольника SAB.

Рис. 2. Пример решения задачи 16 участника ЕГЭ 2015 года
2. Неверное определение искомого угла между прямой и плоскостью (неверный переход к планиметрической задаче) стало также одной из наиболее распространенных типовых ошибок при выполнении пункта б) задачи 16. Процедура определения угла между прямой и плоскостью требует особых рассуждений и дополнительных построений (проекции прямой на плоскость). Однако многими учащимися искомый угол между прямой и плоскостью был определен интуитивно, без необходимых умозаключений, что, чаще всего, было ошибочным и сводило все решение пункта б) к 0 баллов.
Приведем пример. Решение пункта б) задачи 16 на рисунке 3 оценено 0 баллов, т.к. искомый угол между прямой SC и плоскостью ASB определен неверно. Учащимся даже предпринята попытка построения искомого угла по всем правилам – проведен перпендикуляр (видимо, с целью построения проекции прямой на плоскость), но, к сожалению, не из точки С, а из точки А. Это, вероятно, говорит о том, что у учащегося есть некоторое общее представление об угле между прямой и плоскостью, но недостаточно полное. Часто в решениях пункта б) отсутствовали необходимые дополнительные построения искомого угла, а сам угол просто констатировался (неверно) учащимся без каких-либо пояснений. Все эти случаи сводились к 0 баллов.
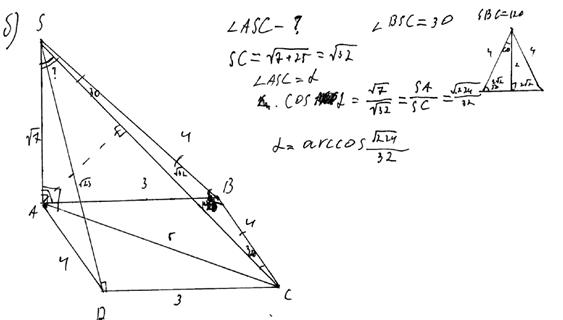
Рис.3. Пример решения задачи 16 участника ЕГЭ 2015 года
3. Распространенным недостатком в решении задачи 16 было отсутствие теоретических ссылок и обоснований логических переходов. Учащиеся не указывали используемую для вывода теорию: определения, теоремы, признаки, свойства и т.д.
Решение задачи 16 чаще всего представляло собой констатацию фактов, без аргументации, что недопустимо в решениях геометрических задач. Хотя иногда в работах учащихся имели место некоторые обоснования выводов (в частности, ссылки на теорему Пифагора, теорему о трех перпендикулярах и др.), но основания для этого не приводились или были недостаточно полными.
Таким образом, на основе анализа типичных ошибок в решениях задачи 16 участников ЕГЭ по математике профильного уровня в 2015 году в Алтайском крае среди причин их появления можно выделить главную – недостаточное владение теоретическим материалом, и как следствие, отсутствие ссылок на теоретические положения при решении задач. Кроме того, оставляет желать лучшего пространственное воображение учащихся, грамотность чертежей, их обоснованность. Следует отметить и формализм при решении стереометрических задач.
Для предупреждения этих ошибок целесообразно при изучении геометрии в основной и старшей школе требовать от учащихся указания (письменно) и формулировок (устно) используемых аксиом, определений, теорем, свойств, признаков при решении каждой задачи. Кроме того, для учащихся с разным уровнем подготовки должны быть выстроены принципиально разные стратегии подготовки к профильному экзамену, необходима дифференциация обучения, разработка стратегии обучения и подготовки к выпускному экзамену с учетом уже имеющегося у выпускника уровня образовательной подготовки. Прежде всего, учителю необходимо познакомиться со структурой и содержанием КИМов, сравнить их с содержанием программного материала и того учебника, по которому учатся школьники. Целесообразно организовать еще и индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований [1].
Однако, можно выделить и позитивные изменения в результатах решения задачи 16 участниками ЕГЭ профильного уровня в Алтайском крае. Следует отметить, что по сравнению с 2015 годом при решении задачи 16 в Алтайском крае улучшилась ситуация с указанием верного ответа. В 2014 году одной из распространенных ошибок было выписывание в ответ на требование «Найдите угол между…» значения одной и тригонометрических функций, используемых в решении, что вело к потере баллов, т.к. решение признавалось незавершенным. В 2015 году таких ошибок практически не было.
Еще одним достоинством решений задачи 16 в 2015 году участниками ЕГЭ в Алтайском крае было активное использование учащимися нестандартных (для школьного курса геометрии) способов решения (в том числе: координатный, векторный, координатно-векторный способы) и др. Также можно констатировать увеличение количества работ с оригинальным решением задачи 16. Приведем пример одного из них.
Решение на рисунке 4 достаточно грамотное. Для нахождения уравнения плоскости по трем точкам учащийся демонстрирует умение работать с определителем, несвойственное школьному курсу математики. Хотя ответ не преобразован, не приведен к эталонному 450, он является правильным, поэтому задание оценено высшим баллом.
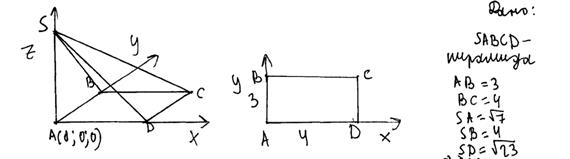
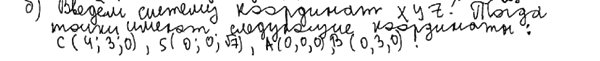

Рис. 4. Пример решения задачи 16 участника ЕГЭ 2015 года
Таким образом, для повышения качества результатов ЕГЭ по математике в Алтайском крае проведен подробный анализ типичных погрешностей и ошибок в решениях участников экзамена, намечены пути их устранения и предотвращения, рассмотренные в настоящей статье на примере задачи 16 профильного уровня. В целом, эта задача является доступной учащимся со средним и хорошим уровнем подготовки по предмету, поэтому учителям целесообразно вести активную работу по подготовке школьников к ее решению с учетом анализа работ участников экзамена в предыдущие годы. С этой целью результаты ЕГЭ по математике профильного уровня в Алтайском крае (в том числе задачи 16) пройдут обсуждение на заседаниях методических объединений учителей математики г. Барнаула и педагогических советах в 2015-2016 году.
Рецензенты:
Овчаров А.В., д.п.н., профессор, директор института физико-математического образования ФГБОУ ВО «Алтайский государственный педагогический университет» Министерства науки и образования РФ, г. Барнаул;
Пышнограй Г.В., д.ф.-м.н., профессор, заведующий кафедрой математического анализа и прикладной математики, ФГБОУ ВО «Алтайский государственный педагогический университет» Министерства науки и образования РФ, г. Барнаул.



