Авторами предлагается технология компьютерной реализации моделей динамического программирования, изучаемых на дисциплинах «Оптимизация в управлении» студентами факультета математики, физики и информатики Тульского государственного педагогического университета им. Л.Н. Толстого и «Исследование операций» студентами Тульского филиала Финуниверситета.
При изучении решения задач динамического программирования целесообразно использовать проблемно ориентированный подход. Перед студентами ставится экономическая задача, необходимо построить ее математическую модель, используя математические методы оптимизации и возможности электронных таблиц MS Excel, найти ее решение. Электронные таблицы наиболее наглядно отражают операции, проводимые с данными, поэтому обучающиеся, проходя шаги алгоритма и указывая ячейки с данными, с которыми проводятся действия, сами участвуют в построении алгоритма вычислений. Это позволяет четко представить пошаговый процесс, используемый в задачах динамического программирования, не отвлекаясь на процесс вычислений. Отметим, что данная статья выполнена в рамках договора о творческом сотрудничестве Тульского филиала Финуниверситета с ТГПУ им. Л.Н. Толстого. Преподаватели принимают участие в таких видах работы, как совместные исследования по научно-методическим темам [3, 4], проведение научно-практических конференций.
При преподавании дисциплин в условиях компетентностного подхода от преподавателя требуется применение инновационных технологий [5], определенных форм обучения, информационных технологий, чтобы завладеть вниманием студентов [1, 2, 6].
Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы. Начало развития ДП относится к 1950-м гг. и связано с именем Р. Беллмана. Рассмотрим конкретный пример.
Задача. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S0=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k-му предприятию (k=1, 2, 3, 4), приносит в конце года прибыль fk(X). Функции fk(X) заданы таблично:
|
Х |
f1(X) |
f2(X) |
f3(X) |
f4(X) |
|
1 2 3 4 5 |
8 10 11 12 18 |
6 9 11 13 15 |
3 4 7 11 18 |
4 6 8 13 16 |
Принято считать, что:
1) прибыль fk(X) не зависит от вложенных средств в другие предприятия;
2) прибыль от каждого предприятия выражается в одних условных единицах;
3) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.
Решение. Обозначим через Xk количество средств, выделенных k-му предприятию. Суммарная прибыль равна:
![]()
Переменные X удовлетворяют ограничениям:
![]() ,
,![]()
![]()
Требуется найти переменные X1, X2, X3, X4, удовлетворяющие данным ограничениям и обращающие в максимум функцию Z.
Рассмотрим особенности модели. Ограничения линейные, но переменные целочисленные, а функции fk(Xk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств можно рассматривать как 4-шаговый, номер шага совпадает с номером предприятия; выбор переменных X1, X2, X3, X4 – уравнения соответственно на I, II, III, IV шагах; S4 – конечное состояние процесса.
Введем в рассмотрение функцию Zk* (Sk-1) – условно оптимальную прибыль, полученную от k-го, (k+1)-го, ..., 4-го предприятий, если между ними распределялись оптимальным образом средства Sk-1 (0 £ Sk-1 £ 5). Уравнения на k-ом шаге удовлетворяют условию: 0 £ Xk£Sk-1 (либо k-му предприятию ничего не выделяем, Xk=0, либо не больше того, что имеем к k-му шагу, Xk £ Sk-1).
Решение уравнений Беллмана осуществляется путем последовательной оптимизации каждого шага.
Компьютерная реализация
Создадим текстовую форму – таблицу для ввода условий задачи. Введем исходные данные задачи в созданную форму-таблицу:
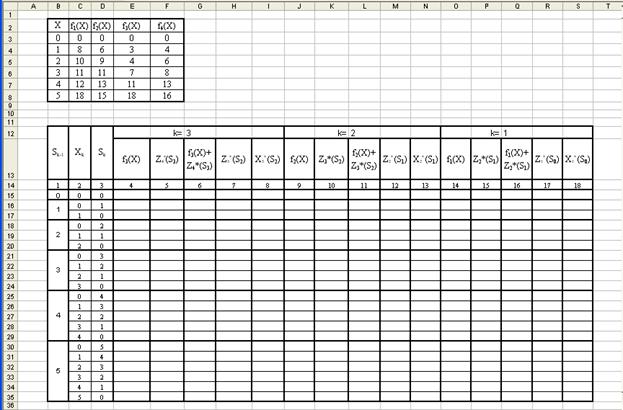
1. В ячейку E15 введем формулу
=ИНДЕКС($B$3:$F$8; ПОИСКПОЗ($C15;$B$3:$B$8); G$12+1), скопируем формулу с ячейки E15 до ячейки Е35.
2. В ячейку F15 введем формулу
=ИНДЕКС($B$3:$F$8;ПОИСКПОЗ($D15;$B$3:$B$8);5),
скопируем формулу с ячейки F15 до ячейки F35.
3. В ячейку G15 введем формулу =E15+F15, скопируем формулу с ячейки G15 до ячейки G35.
4. Находим максимальное значение для каждого состояния от 0 до 5, для этого в ячейку Н15 введем формулу =МАКС(G15). После копирования формулы в ячейку H16 необходимо изменить диапазон с G16 на G16:G17, для этого стоя в строке формул необходимо растянуть выделенный прямоугольник на одну ячейку вниз. Затем копируем формулу из H16 в ячейку H18 и проводим такие же операции по увеличению диапазона, и так до ячейки H30.
5. Находим значение управления Хk, которому соответствует максимальное значение функции Zk, для этого в ячейку I15 введем формулу =ИНДЕКС($C15:G15;ПОИСКПОЗ(H15;G15;0);1), скопируем формулу в ячейки I16, I18, I21, I25, I30 постепенно увеличивая диапазон, аналогично тому, как это делалось в пункте 5. Выделяем диапазон ячеек E15:I35 выполняем команду Копировать, устанавливаем курсор в ячейку J15 выполняем команду Вставить.
Изменим формулу функции Z3*(S2). В ячейки K15, K16, K18, K21, K25, K30 введем соответственно максимальные значения предыдущего шага, находящиеся в ячейках H15, H16, H18, H21, H25, H30. В остальные ячейки поместим значения, стоящие в этом же столбце и соответствующие предыдущим Sk. В ячейку K17 копируем значение ячейки K15; в ячейки K19 и K20 – значения K16 и K17; в K22:K24 – K18:K20 и так до ячейки K35. В результате получим таблицу.
6. Выделяем диапазон ячеек J15:N35 выполняем команду Копировать, устанавливаем курсор в ячейку O15 выполняем команду Вставить. Сравнивая полученные значения, получим Z1*(5)=24 усл. ед. = Zmax при X1*= X1*(5)=1. Вычисляя, получим S1* = 5 – 1 = 4, а по таблице в столбце 12 находим X2* = X2* (4) = 2. Далее находим S2* = 4 – 2 = 2, а в столбце 6 X3* = X3*(2) = 1. Наконец, S3* = 2 – 1 = 1 и X4* = X4*(1) = 1, т. е. X*(1; 2; 1; 1).
Ответ. Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед.
Рецензенты:
Добровольский Н.М., д.ф.-м..н., профессор Тульского государственного педагогического университета имени Л.Н. Толстого, г. Тула;
Митрохина О.А., д.п.н., профессор Тульского государственного педагогического университета имени Л.Н. Толстого, г. Тула.



