В работе [1] было показано, что обрезание потенциала Морзе, который моделирует ковалентную компоненту связи Si-Oв кварцевом стекле, позволяет получать модели стекол со значениями плотности, близкими к экспериментальным значениям (2.2 г/см3) даже при высоких скоростях закалки, характерных для численных экспериментов (10-2-101К/пс). Т.е.эмпирические потенциалы с укороченными «хвостами» позволяют более корректно описывать процессы перестройки связей в процессе стеклообразования и получать в конечном итоге «правильный» объем системы при ее охлаждении в рамках NPT-процесса.
К сожалению, объем (плотность) системы – интегральный параметр, не позволяющий оценить все детали структурных изменений в стекле, возникающих при введении обрезания потенциалов межатомных взаимодействий. Поэтому в данной работе рассчитаны и проанализированызависимости основных структурных параметров моделей стекол от радиуса обрезания межатомных потенциалов.
Методика получения моделей кварцевого стекла
Методика получения моделей, потенциалы межатомных взаимодействий и их параметризация подробно изложены в работе[1]. Целью данной работы является изучение влияние радиуса обрезания r1потенциала Морзе на основные структурные параметры конечных моделей стекол. Поэтому варьировался единственный параметрr1. Он изменялся в диапазоне от 2.5 до 5.0 Å с шагом 0.1 Å. Значения остальных макроскопических параметров (температурные режимы, скорость закалки, количество атомов и т.п.) были фиксированы. Для каждого значения r1 создавалось шесть образцов, отличающихся начальными значениями координат и скоростей атомов в исходном (расплавленном) состоянии. По этим шести образцам в дальнейшем производилось усреднение рассчитанных параметров. Каждый образец содержал 1000 атомов кремния и 2000 атомов кислорода. Использовалась кубическая расчетная ячейка с периодическими граничными условиями.
Все модели стекол были получены в следующем режиме. Начальная температура 6000 К, давление – 1 атм. После небольшого периода релаксации (0.2 нс) каждый образец независимо охлаждался до комнатной температуры в течение 10 нс при постоянном давлении (1 атм). После релаксации при комнатной температуре и атмосферном давлении (0.2 нс) производилось усреднение координат каждого атома в процесс его теплового движения в течение 10 пс. Эти усредненные координаты атомов затем использовались для расчетаструктурных параметров модели.
Динамика атомов рассчитывалась при помощи пакета HOOMD-blue [3, 5], реализующего параллельные вычисления на графических процессорах при помощи технологии CUDA [2].
Результаты
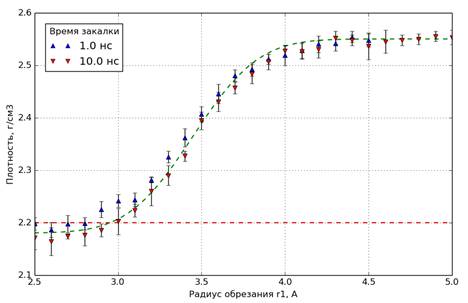
Как уже отмечалось выше, в работе [1] было показано, что укорачивание «хвостов» потенциала Морзе приводит к уменьшению плотности результирующих стекол. При этом охлаждение системы производится при постоянном давлении. При значении радиуса обрезания r1 ~ 3 Åи менее, плотность становится близкой к экспериментальному значению 2.2 г/см3[8].В данной работе время закалки было увеличено на порядок (10 нс по сравнению с 1 нс в [1]). Для сравнения на рис.1 приведены зависимости плотности кварцевого стекла от радиуса обрезаниядля двух значений скорости закалки.
|
|
|
Рис.1. Зависимости плотности кварцевого стекла от радиуса обрезания для двух значений времен закалки. 1 нс – из работы [1] и 10 нс –из данной работы. Пунктир – экспериментальное значение плотности кварцевого стекла (2.2 г/см3) |
Видно, что зависимости плотности от радиуса обрезания при различных скоростях закалки близки друг к другу, иплотность приближается к экспериментальному значению при r1 ≤ 3.0-3.1 Å.
Для оценки влияния радиуса обрезания межатомных потенциалов на параметры ближнего порядка кварцевого стекла (т.е. на параметры его структурных элементов - кремний-кислородных тетраэдров) были рассчитаны средние длины связей Si-O, O-O и углы O-Si-O, которые представлены в таблице ниже. Усреднение выполнялось по всем полученным в данной работе моделям (26 значений параметра r1в диапазоне 2.5-5.0 Å и 6 вариантов для каждого r1, т.е. всего по 156 моделям).
|
|
Данная работа |
Из литературы |
|
Длина связейSi-O, Å |
1.617±0.003 |
1.62 [7] |
|
Угол O-Si-O, град |
108.85±0.02 |
109.47 |
|
Длина связей O-O, Å |
2.635±0.006 |
2.65 [7] |
Как видно из таблицы, значения близки к литературным данным, а вариации значений очень малы (доли процента для длин связейSi-Oи O-O). Это говорит о том, что обрезание потенциалов межатомного взаимодействия практически не сказывается на ближнем порядке. Обнаружена только одна значимая особенность, связанная с влиянием радиуса обрезания на ближний порядок. Это поведение парных радиальных функций распределения по кислородусправа от первого пика, соответствующего распределению длин ребер кремний-кислородных тетраэдров (связь O-O). Эта особенность отмечена на рис.2.
|
|
|
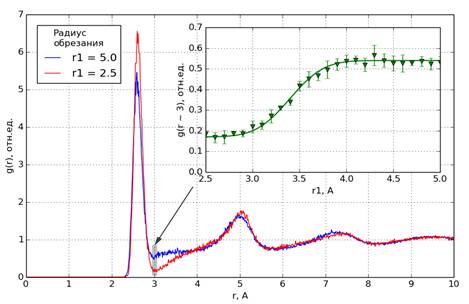
Рис.2. Парные радиальные функции распределения O-O для двух значений радиуса обрезаний. Во врезке – зависимость высоты правого «плеча» пика O-O в области r~3 от радиуса обрезания |
На основной диаграмме рис.2 представлены две радиальные функции распределения, соответствующие двум радиусам обрезания r1 = 5 Å и r1 = 2.5 Å. Видно, что высота «плеча» справа от пика 2.6 Åдля этих двух случаев заметно различается. На врезке представлена зависимость радиальной функции распределения (усредненной в диапазоне 2.95 ≤r≤ 3.05)от радиуса обрезания r1. Область усреднения помечена на основном графике серым цветом. Хорошо виден «ступенчатый» характер поведения высоты плеча при изменении r1. При уменьшении радиуса обрезания высота плеча уменьшается почти в три раза, а сам пик 2.6 Åувеличивается. Таким образом, разброс длин ребер кремний-кислородных тетраэдров в моделях, получаемых при помощи потенциалов с укороченными хвостами (при r1< 3Å), заметно меньший, чем в моделях, получаемых при помощи исходных потенциалов (r1>4Å). Т.е. такие модели состоят из более «регулярных» тетраэдров.
Рассмотрим теперь влияние обрезания потенциалов на «упаковку» структурных элементов. Одним из чувствительных параметров, характеризующих «упаковку», является функция распределения углов Si-O-Si. Эти распределения для двух значений радиусов обрезания представлены на рис.3.
|
|
|
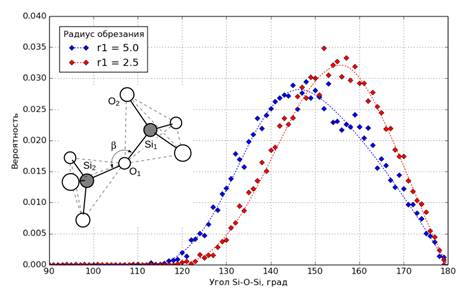
Рис.3. Функции распределения углов Si-O-Si(β) для двух значений радиуса обрезания |
Видно, что максимум функции распределения для моделей, полученных при помощи «обрезанных» потенциалов (r1 = 2.5 Å), заметно смещен в сторону больших значений по сравнению с моделями, полученными с исходными потенциалами Морзе (r1 = 5.0Å). К сожалению, в настоящее время отсутствуют прямые экспериментальные методы измерения распределения углов Si-O-Siв аморфных системах типа кварцевого стекла. Существующие в литературе данные дают достаточно большой разброс положения максимума – от 140˚ до 160˚ (см., например, обзор в работе [6]).Поэтому непосредственное сравнение с экспериментом по этому параметру затруднительно. Тем не менее, тенденция к «распрямлению» связей Si-O-Siпри введении обрезания межатомных потенциалов очевидна.
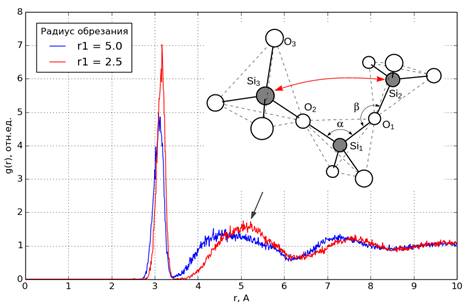
На рис.4 приведены парные радиальные функции распределения атомов кремния, представляющих центры кремний-кислородных тетраэдров. Второй пик в области 5 Å соответствует распределению расстояний кремний-второй кремний (т.е. между центрами тетраэдров, соединенных третьим тетраэдром, что схематично показано на врезке). Видно, что для моделей, полученных припомощи обрезанных потенциалов (r1 = 2.5 Å), этот пик становится более выраженным, смещается вправо, а его максимум приближается к экспериментальному значению 5 Å [7].
|
|
|
Рис.4. Парные радиальные функции распределения Si-Si для двух значений радиуса обрезаний |
Выводы
Как было показано в работе [1], обрезание длинных хвостов потенциала Морзе, моделирующего ковалентную компоненту связи Si-O, позволяет получать модели кварцевых стекол, плотность которых приближается к экспериментальному значению. Тем не менее, оставался открытым ряд вопросов о влиянии такой модификация потенциалов на основные структурные параметры стекол. Приведенные выше данные позволяют ответить на некоторые из них и сформулировать следующие выводы.
1. Обрезание хвостов потенциала Морзе не влияет на средние параметры ближнего порядка, такие как длина связей Si-O и углы O-Si-O.
2. Обрезание приводит к уменьшению разброса длин ребер кремний-кислородных тетраэдров. Т.е. модели состоят из более регулярных тетраэдров.
3. Обрезание хвостов оказывает заметное влияние на упаковку структурных элементов: за счет распрямления связей Si-O-Siувеличиваются расстояния между центрами тетраэдров, уменьшается разброс этих расстояний. В целом, можно предположить, что модели, получаемые при помощи потенциалов с укороченными хвостами, представляют собой более регулярные пространственные сети кремний-кислородных тетраэдров, нежели модели, получаемые при помощи исходных потенциалов.
Рецензенты:Парфенов О.Г., д.т.н., заведующий лабораторией плазмохимии и проблем материаловедения Института химии и химической технологии СО РАН. Россия, г. Красноярск;
Белобров П.И., д.ф.-м.н., с.н.с., профессор кафедры биофизики СФУ, в.н.с.Института биофизики СО РАН, Россия, г. Красноярск.