Наиболее важным этапом при оценке эффективности воздействия на биологически активные точки (БАТ) является выбор математических моделей ее основных элементов и сигналов, циркулирующих в системе, так как они осуществляют взаимосвязь между системой, в которой будут использоваться результаты, и областями математических абстракций, в которых эти результаты получены. Эффективность применения полученных результатов будет существенным образом зависеть от достоверности, с которой математические модели описывают реальную ситуацию. В большинстве практических случаев построение точной модели представляет серьезные трудности и приводит к значительному ее усложнению. С другой стороны, необоснованное упрощение математической модели может привести к значительным погрешностям в оценке эффективности разработанных на ее основе модели БАТ.
Задачей исследования является повышение диагностической эффективности проведения измерений с использованием биологически активных точек.
В настоящее время разработаны ряд моделей БАТ, позволяющих провести анализ и синтез существующих и разрабатываемых устройств и приборов, воздействующих с заданными требованиями на БАТ без потери основных эффектов, имеющих место в реальной ситуации с учетом нелинейности тракта распространения волн [7, 4]. Анализ этих моделей с учетом особенностей энергетических функций кожи позволяет ввести в математические модели измерения электрических параметров сигналов ряд допущений, упрощающих оценку эффективности энергоинформационной системы человека.
К ним можно отнести:
1. Энергоинформационная система человека является дискретной М-ичной системой передачи информации с ограниченным алфавитом источника.
2. Процесс на входе БАТ является узкополосным.
3. Основным элементом энергоинформационной системы человека, вносящим амплитудные и фазовые искажения является БАТ, амплитудно-амплитудная и амплитудно-фазовая, характеристики которой в соответствии с выбранной методикой анализа описывается нелинейной характеристикой.
4. Амплитудные и фазовые характеристики БАТ в полосе частот, занимаемых входным процессом инвариантны к временным и частотным изменениям.
5. БАТ как нелинейный элемент может быть представлена в соответствии с теоремой Винера в виде последовательного соединения безынерционной нелинейной и инерционной линейной частей.
6. В энергоинформационной системе человека наряду с полезными воздействиями на БАТ и мешающими воздействиями присутствует нормальный белый шум.
7. Сигналы и помехи при распространении в БАТ не подвержены значительным флюктуациям, и на интервале оценки параметров сигнала их амплитуды можно считать постоянными.
Введенные допущения позволяют наложить ряд ограничений на математическую модель нелинейных взаимодействий, происходящих в БАТ, к которым можно отнести:
1. С целью анализа влияния электропунктурной диагностики собственно нелинейных эффектов БАТ будем рассматривать как безынерционный нелинейный элемент, полностью характеризующийся мгновенными передаточными характеристиками, измеренными в односигнальном режиме.
2. Сигналы и помехи могут быть представлены квазигармоническими процессами с равномерными законами распределения начальных фаз. Преимущество такого представления заключается в том, что при анализе учитываются не только статистические характеристики параметров сигнала, но и его конкретный вид.
С учетом введенных допущений модель исследуемой системы может быть представлена в следующем виде (рисунок 1)
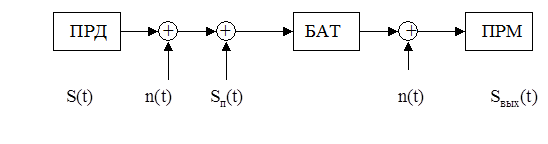
Рис. 1. Модель воздействия на биологически активную точку
ПРД – передающая часть прибора для электропунктуры;
ПРМ – приемная часть прибора для электропунктуры;
БАТ – биологически активная точка, описываемая нелинейной амплитудной характеристикой вида g(u);
S(t) – входной сигнал;
n(t) – белый шум;
Sп(t) – мешающее воздействие
Sвых(t) – выходной сигнал.
В соответствии с [6] сигнал на выходе системы может быть записан в виде
![]()
![]() (1)
(1)
![]() − соответственно k-тые полезное и мешающее воздействия, представляющие собой интегрируемые в квадрате функции;
− соответственно k-тые полезное и мешающее воздействия, представляющие собой интегрируемые в квадрате функции;
![]() − коэффициенты передачи k-тых сигнала и помехи;
− коэффициенты передачи k-тых сигнала и помехи;
![]() − соответственно задержки и текущие фазы k-того сигнала (помехи) относительно времени прихода и фазы измеряемого сигнала;
− соответственно задержки и текущие фазы k-того сигнала (помехи) относительно времени прихода и фазы измеряемого сигнала;
n(t) – нормальный белый шум с нулевым математическим ожиданием и спектральной плотностью N0.
С учетом введенных допущений процесс на выходе БАТ полностью определяется огибающей входного процесса (1) и амплитудно-амплитудной и амплитудно-фазовой характеристиками БАТ и может быть записан в виде:
![]() (2)
(2)
где ![]() − огибающая входного процесса;
− огибающая входного процесса;
![]() − фаза входного процесса.
− фаза входного процесса.
Выражения (1) и (2) позволяют анализировать не только результирующее воздействие входного сигнала, но и тонкую структуру выходного процесса с определением амплитудных и фазовых характеристик каждой из его составляющих [2,3,5,6].
С учетом (1) входной сигнал может быть представлен в виде:
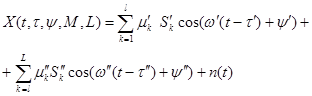 (3)
(3)
Подставляя (3) в (2) получим:
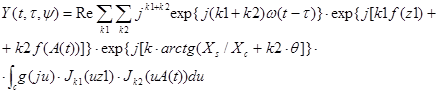 (4)
(4)
где A(t),![]() − огибающая и фаза нормального белого шума;
− огибающая и фаза нормального белого шума;
Xs,Xc – синфазная и квадратурная составляющие входного процесса;
Jk() – функция Бесселя.
Выражение (4) определяет выходной процесс через огибающие и фазы входных сигналов, помех и входного шума. Данное выражение является удобным для определения статистических характеристик выходного процесса, необходимых для оценки методов акупунктуры, однако не позволяет анализировать тонкую структуру отдельных компонент выходного процесса, что может привести к значительным ошибкам при анализе полученных результатов.
Для определения тонкой структуры выходного процесса воспользуемся «теоремой сложения» для Бесселевых функций [1], которая применительно к (4) имеет вид:
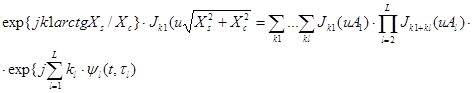 (5)
(5)
Выражение (5) совпадает с выражением, определяющим тонкую структуру процесса на выходе нелинейного элемента, полученного в [5], что показывает правомерность использования «теоремы сложения».
В соответствии с требованиями, предъявляемыми к приборам измерения параметров БАТ, в качестве показателя эффективности будем использовать полную среднюю вероятность ошибочной регистрации, которая с учетом введенных ограничений для l-го сигнала будет определяться выражением:
![]() (6)
(6)
G(x) – область изменения параметров входного процесса;
![]() − совместная плотность вероятности параметров выходного процесса;
− совместная плотность вероятности параметров выходного процесса;
![]() − условная вероятность ошибки регистрации при постоянстве параметров сигнала.
− условная вероятность ошибки регистрации при постоянстве параметров сигнала.
В случае воздействия мешающих сигналов вероятность ошибочной регистрации зависит не только от статистических и энергетических характеристик параметров сигналов и помех, но и от коэффициента взаимной корреляции между ними, который может быть представлен в следующем виде:
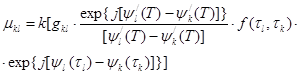 (7)
(7)
где
![]()
Таким образом, для нахождения ошибки регистрации необходимо знание статистических характеристик и коэффициента взаимного различия выходного процесса.
Анализ (7) показывает, что величина коэффициента взаимного различия в существенной степени зависит от уровня интермодуляционных компонент, возникающих из-за нелинейности амплитудной характеристики БАТ. Уровень этих компонент зависит как от уровня входных сигналов, так и конкретного вида амплитудной и фазоамплитудной характеристик БАТ.
Оценим влияние вида амплитудной характеристики канала на величину коэффициента взаимного различия с целью определения вида амплитудной характеристики, при котором обеспечивается максимальное значение этого коэффициента.
В дальнейшем будем рассматривать лишь практически интересные случаи, для которых амплитудные характеристики каналов являются нечетными и при больших значениях аргумента стремятся к нулю.
В этом случае амплитуды сигналов на выходе БАТ преобразуется к виду:
![]() (8)
(8)
где f(x) – мгновенная амплитудная характеристика.
Воспользовавшись разложением функции Бесселя в степенной ряд [1] с учетом того, что в области первой гармоники ![]() , получим
, получим
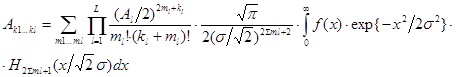 (9)
(9)
где Hn(z) –полиномы Эрмита.
Мгновенную амплитудную характеристику нелинейного элемента представим в виде:
![]() (10)
(10)
Тогда выражение (9) приводится к виду:
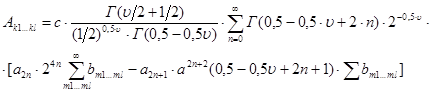 (11)
(11)
где
с = Г(3/2),
![]() ,
,
![]() .
.
Согласно [1] ряд (11) является сходящимся с положительными членами и, следовательно, наилучшим, с точки зрения получения максимального значения коэффициента взаимного различия, является нелинейный элемент, обеспечивающий максимальное значение n-го члена:
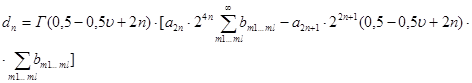
(12)
Для нахождения максимального значения dn необходимо решить уравнение:
![]() (13)
(13)
Решение (13) связано со значительными трудностями из-за сложного характера an и bm1…ml, однако известно [3], что уровень интермодуляционных составляющих зависит от количества взаимодействующих сигналов и будет наибольшим при двухсигнальном входном воздействии при прочих равных условиях, а в двухсигнальном режиме коэффициент взаимного различия будет определяться величиной А12 и будет наибольшим при равенстве входных сигналов. С учетом вышеизложенного, полагая в (13) n=0, получим уравнение для определения вида амплитудной характеристики:
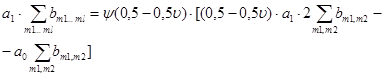 (14)
(14)
которое имеет решение при ![]() .
.
Следовательно, для обеспечения максимального значения коэффициента различия или иными словами, для обеспечения получения наилучших результатов, необходимо, чтобы сквозная характеристика измеряемой схемы, включающей БАТ, описывалась характеристикой идеального ограничителя. Дополнительный нелинейный элемент для обеспечения заданной сквозной характеристики может быть введен на вход приемного устройства.
Рецензенты:
Сербина Л.И., д.ф.-м.н., профессор кафедры математики и информатики ГБОУ ВО «Ставропольский государственный педагогический институт» Министерства образования и молодежной политики Ставропольского края, г. Ставрополь;
Тинькова Е.Л., д.б.н., доцент, зав. кафедрой биологии и экологии ГБОУ ВО «Ставропольский государственный педагогический институт» Министерства образования и молодежной политики Ставропольского края, г. Ставрополь.



