Задача обеспечения оптимального теплового режима относится к одной из важнейших задач проектирования, так как температура электронных элементов оказывает существенное влияние на надежность их функционирования [1]. Существует ряд способов решения данной задачи: снижение потребляемой мощности; активное охлаждение; пассивное охлаждение; рациональное размещение источников тепла.
Цель исследования
В данной работе рассматривается задача повышения надежности за счет оптимизации теплового режима печатной платы путем рационального размещения электронных элементов, являющихся источниками тепла.
Материал и методы исследования
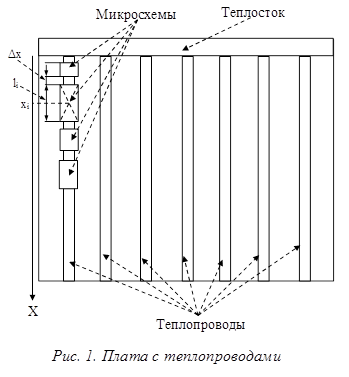
В статье рассматривается вариант конструкции платы, представленный на рисунке 1. Плата имеет диэлектрическое основание, на котором наклеены в виде полос медные однотипные теплопроводы. Разногабаритные в общем случае интегральные микросхемы устанавливаются на теплопроводы, по которым отводится в одном направлении большая часть выделяемой ими тепловой энергии. Коэффициент теплопроводности материала теплопроводов на три порядка больше, чем материала платы. Хороший тепловой контакт интегральных микросхем с теплопроводом обеспечивается применением теплопроводной пасты. Плата эксплуатируется в разряженной атмосфере.
Указанные особенности конструкции и условий эксплуатации позволяют ввести следующие допущения: 1) теплопровод с источниками тепла теплоизолирован со всех сторон, кроме соединения с теплостоком; 2) тепловое контактное сопротивление между теплопроводом и источником тепла (корпусом микросхемы) не зависит от места его расположения на теплопроводе, и его влиянием на перегрев источника тепла можно пренебречь; 3) тепловой поток через поверхность контакта источника с теплопроводом однороден.
Введенные допущения позволяют рассмотреть каждый теплопровод в отдельности для определения оптимального порядка расположения на нем микросхем.
В [3] было выведено условие расположения микросхем на теплопроводе для стационарного теплового режима, минимизирующее максимальный перегрев теплопровода vтmax → min:
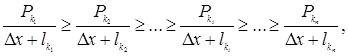(1)
где 
- мощность рассеивания i-го по порядку источника, считая от теплостока;
- расстояние между источниками;
- размер (по оси Х) i-го по порядку источника, считая от теплостока.
Рассмотрим теперь задачу расположения микросхем (источников тепла) на теплопроводе минимизирующего интенсивность отказов электронного устройства.
Интенсивность отказов электронных элементов является в общем случае нелинейной функцией температуры. В диапазоне рабочих температур электронного аппарата зависимость интенсивности отказов электронных элементов от температуры может быть аппроксимирована линейной функцией вида [4]:
λi(ti)= λi0+ki(ti-t0),
где λi(ti) - интенсивность отказов i-го электронного элемента при его рабочей температуре ti; λi0 - интенсивность отказов i-го электронного элемента при температуре окружающей среды t0; ki - коэффициент линеаризации.В [2] показано, что задачу размещения n источников тепла (электронных элементов), минимизирующего интенсивность отказов аппарата, можно свести к минимизации выражения:
, (2)
где vi – перегрев i-го электронного элемента относительно окружающей среды.
С учетом принятых выше допущений перегрев i-го по порядку источника тепла (интегральной микросхемы) относительно теплостока в точке с координатой (xi+li/2) можно определить по формуле:
vi= viсоб + v-iнав + v+iнав , (3)
где viсоб - собственный перегрев; v-iнав – перегрев, наведенный источниками тепла, стоящими на теплопроводе ближе к теплостоку, чем i-й по порядку источник; v+iнав - перегрев, наведенный источниками, стоящими на теплопроводе относительно теплостока дальше, чем i-й по порядку источник.
Вычисление трех составляющих выражения (3) осуществляется по формулам:
; 
;
,
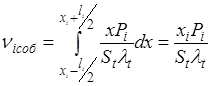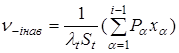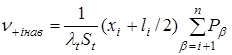где 
- координаты центра посадочного места соответственно i-го, a-го и b-го по порядку источника; 
- мощности рассеивания соответственно i-го, a-го и b-го по порядку источника; St – площадь сечения теплопровода; lt – коэффициент теплопроводности материала теплопровода; n – количество источников на теплопроводе.
Для решения задачи (2) предлагается использовать метод ветвей и границ. При этом нижняя граничная оценка на нулевом шаге может быть вычислена следующим образом. Сначала все источники располагаются на теплопроводе в порядке, соответствующем требованию выражения (1), и для каждого из них вычисляется перегрев для нулевого шага 
(i = 1, 2,…, n). После этого величины 
упорядочиваются по неубыванию 
, а величины ki – по невозрастанию 
.
В качестве нижней граничной оценки на нулевом шаге принимаем величину:
. (4)
Далее все множество решений разбивается на n подмножеств:
.
Для каждого подмножества вычисляется нижняя граничная оценка. Подмножество 
включает в себя множество решений, когда первым по порядку стоит i-й источник (электронный элемент). Оценка подсчитывается следующим образом. Первым располагается i-й источник, а оставшиеся размещаются в порядке, соответствующем условию (1). Для всех электронных элементов вычисляются значения перегревов по формуле (3) и выполняется процедура, аналогичная вычислению 
. При этом нижняя граничная оценка уточняется:
. (5)
Для уменьшения трудоемкости вычислений можно ограничиться поиском вглубь на дереве решений, выбирая для ветвления каждый раз вершину с меньшей граничной оценкой.
Использование метода ветвей и границ позволяет найти одно из нехудших решений, а также получить оценку близости этого решения к оптимальному, сравнивая величины оценок на нулевом и последнем шаге.
Результаты исследования и их обсуждение
Рассмотрим пример использования предложенного метода. Чтобы не загромождать статью чрезмерным количеством расчетов, рассмотрим случай размещения на теплопроводе 5 микросхем. В таблице 1 приведены исходные параметры, необходимые для решения задачи предложенным методом (Δx=4 мм). Принятые значения коэффициентов ki согласуются с данными, приведенными в [5].
Таблица 1
Исходные параметры
|
Обозначение микросхемы |
Длина микросхемы l (мм) |
Мощность рассеивания P (вт) |
Отношение P/(l+Δx) (Вт/мм) |
Коэффициент линеаризации k *10-6 (град-1час-1) |
|
ИС 1 |
20 |
1,5 |
0,0625 |
0,015 |
|
ИС 2 |
30 |
2 |
0,0588 |
0,018 |
|
ИС 3 |
16 |
1,3 |
0,065 |
0,0020 |
|
ИС 4 |
20 |
1,2 |
0,050 |
0,025 |
|
ИС 5 |
14 |
0,9 |
0,050 |
0,012 |
Будем считать, что теплопровод медный (λt=380 вт/м* град) и площадь его сечения St= 0,000015 м2. В таблице 2 приведены результаты расчета перегревов микросхем по формуле (3) при их расположении, удовлетворяющем условию (1), и нижняя граничная оценка, рассчитанная по формуле (4):
=0,025*10-6*22,386+0,020*10-6*43,333+0,018*10-6*62,526+0,015*10-6*68,053+0,012*10-6*71,000=4,425*10-6 .
Если рассмотреть варианты размещения, когда на первом месте закреплена микросхема ИС 3, то нижняя граничная оценка уточняется по формуле (5):
= 0,020*10-6*22,386+0,025*10-6*43,333+0,018*10-6*62,526+0,015*10-6*68,053+0,012*10-6*71,000=4,529*10-6 .
Таблица 2
Результаты расчета перегревов микросхем
|
Порядок расположения микросхем на теплопроводе |
Координата центра микросхемы (м) |
Коэффициент линеаризации k*10-6 (град-1час-1)
|
Перегрев микросхемы °С |
Нижняя граничная оценка |
|
ИС 3 |
0,012 |
0,020 |
22,386 |
4,425*10-6
|
|
ИС 1 |
0,034 |
0,015 |
43,333 |
|
|
ИС 2 |
0,063 |
0,018 |
62,526 |
|
|
ИС 5 |
0,089 |
0,025 |
68,053 |
|
|
ИС 4 |
0,110 |
0,012 |
71,000 |
Процедуру нахождения варианта размещения при использовании поиска вглубь на дереве решений иллюстрирует рис. 2.
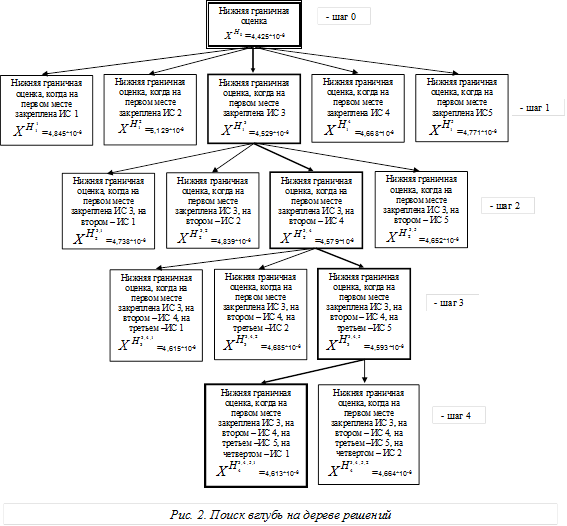
Как видно из рисунка 2, наилучшее решение соответствует порядку размещения микросхем относительно теплостока: ИС 3, ИС 4, ИС 5, ИС 1, ИС 2. При этом можно количественно оценить качество полученного решения, сравнивая 
и 
:
.
Количественная оценка показывает, что значение критерия оптимизации для полученного решения отличается от оптимального решения не более чем на 4,25%.
Выводы
Проведенные исследования позволяют сделать вывод, что предложенный способ может быть использован в задачах размещения электронных элементов на платах с теплопроводами, эксплуатирующихся в условиях, оговоренных выше. Приведенный пример показывает, что за приемлемое количество шагов можно получить достаточно хорошее решение и дать ему количественную оценку.
Рецензенты:
Баламирзоев А.Г., д.т.н., профессор, профессор кафедры математики и информатики Махачкалинского филиала ФГБОУ ВПО «Московский автомобильно-дорожный государственный технический университет (МАДИ)», г. Махачкала.
Кобзаренко Д.Н., д.т.н., заведующий лабораторией информационных технологий в энергетике ФГБУН «Институт проблем геотермии ДНЦ РАН», г. Махачкала.