В работе рассматриваются новые постановки двумерных двухфазных задач со свободными границами в цилиндрической и сферической системах координат. Поставленные задачи Стефана не содержат начальных условий, так как температурное поле определяется только в возмущенной в тепловом отношении области биологической ткани.
При ограничениях на зоны теплового возмущения получены постановки задач Стефана для полуограниченных сред. Условия регулярности на бесконечности при достаточно больших значениях зонах теплового возмущения заменены краевыми условиями Дирихле или Неймана.
1. Осесимметричная криодеструкция
Если охлаждающая поверхность криоинструмента представляет собой круг или полусферу, что наиболее часто встречается в криохирургической практике, то температурное поле в биоткани обладает осевой симметрией и, следовательно, зависит только от двух пространственных координат. В цилиндрической системе координат - ![]() и
и ![]() , в сферической от
, в сферической от ![]() и
и ![]() . Воспользовавшись выражениями для градиента в цилиндрической:
. Воспользовавшись выражениями для градиента в цилиндрической:
![]()
и сферической:
![]()
системах координат, получаем выражения для нормали к изотермической поверхности ![]() ее кажущейся скорости в направлении нормали
ее кажущейся скорости в направлении нормали ![]() и производной
и производной ![]()
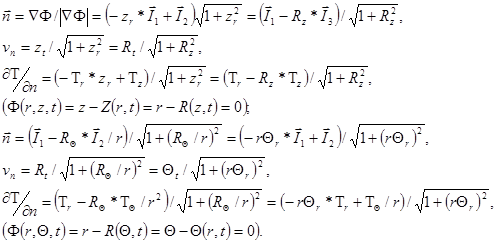
С помощью этих формул легко записываются условия сопряжения ![]() и условие
и условие ![]() на поверхности
на поверхности ![]()
В случае плоского кругового аппликатора температурное поле можно рассматривать как в цилиндрической ![]() , так и в сферической
, так и в сферической ![]() системах координат. Если же охлаждающая поверхность представляет собой полусферу радиуса
системах координат. Если же охлаждающая поверхность представляет собой полусферу радиуса ![]() , то предпочтительной является сферическая система координат, так как поверхность биологической ткани совпадает с координатными поверхностями
, то предпочтительной является сферическая система координат, так как поверхность биологической ткани совпадает с координатными поверхностями ![]() и
и ![]() и
и ![]() . Итак, если криодеструкция осуществляется плоским круговым криозондом, то для
. Итак, если криодеструкция осуществляется плоским круговым криозондом, то для ![]() и соответствующих изотерм получаем нестационарную задачу Стефана [1-3]:
и соответствующих изотерм получаем нестационарную задачу Стефана [1-3]:
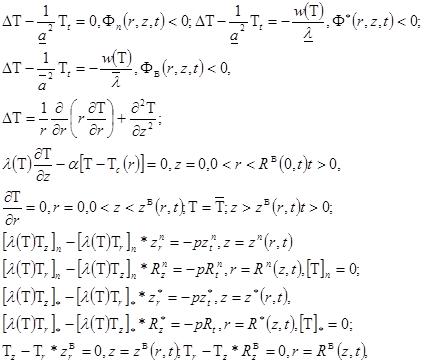
и нестационарную пространственно локализованную задачу Стефана в случае полусферической охлаждающей поверхности криозонда:
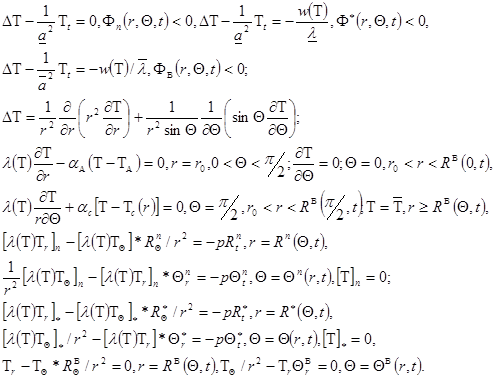
Отметим, что поставленные задачи Стефана не содержат начальных условий, так как температурное поле определяется только в возмущенной в тепловом отношении области биологической ткани ![]() , вырождающейся при
, вырождающейся при ![]()
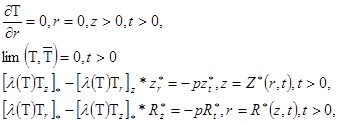
где ![]()
В случае полусферической охлаждающейся поверхности криозонда приходим к следующей двухфазной задаче Стефана [4; 5]:
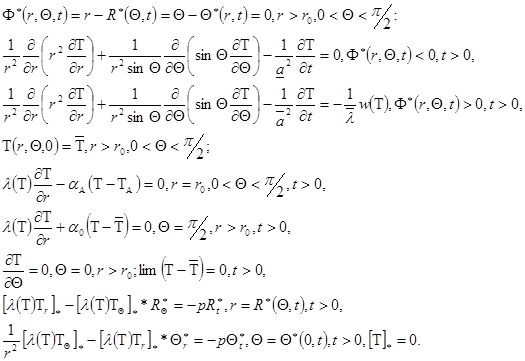
Дальнейшее упрощение задач связано с переходом от неограниченных областей ![]() к квадрату
к квадрату ![]() и сектору
и сектору ![]() .
.
С определенной погрешностью условия регулярности на бесконечности при достаточно больших значениях ![]() и
и ![]() можно заменить краевыми условиями Дирихле
можно заменить краевыми условиями Дирихле
![]()
или Неймана
![]() .
.
Последнее, очевидно, равно нулю в случае пространственно локализованных задач Стефана, если зоны теплового возмущения превосходят максимальный размер установившейся стационарной зоны теплового возмущения биологической ткани, вне которой температурное поле постоянно ![]() .
.
2. Стационарные задачи осесимметричной криодеструкции биоткани
При заданной монотонно понижающейся до некоторого предельного значения температуре аппликатора ![]() максимальные размеры зон криопоражения, замораживания и теплового возмущения достигаются в стационарном состоянии, когда
максимальные размеры зон криопоражения, замораживания и теплового возмущения достигаются в стационарном состоянии, когда ![]() и
и ![]() . Для определения пары функций
. Для определения пары функций ![]() и
и ![]() получаем соответствующие стационарные задачи Стефана [6]:
получаем соответствующие стационарные задачи Стефана [6]:
![]()
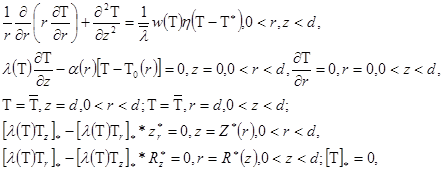
в случае кругового аппликатора и
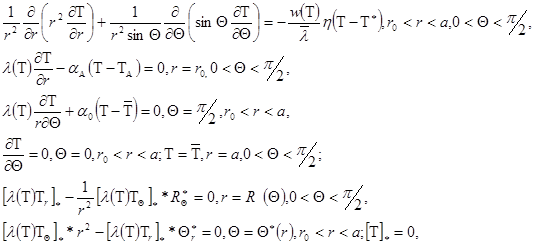
в случае полусферического аппликатора. При ![]() приходим к постановкам задач Стефана для полуограниченных сред
приходим к постановкам задач Стефана для полуограниченных сред ![]() и
и ![]() ,
, ![]() .
.
Рецензенты:
Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН «Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН», г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного геофизического института, г. Нальчик.



