Результаты современных исследований показали, что характеристики гемодинамики, физико-механики и электрофизики сердечно-сосудистой системы, близкие к результатам физиологических экспериментов и клинических наблюдений, достигаются в приближении, что миокард сердца имеет топологию Мебиуса [3; 4; 9]. Это делает актуальным решение задачи по «визуализации» внутренней структуры миокарда сердца.
Известно, что в современной методологии анализа сложных систем при рассмотрении динамических моделей и построении общих законов поведения и управления с целью нахождения новых закономерностей и характеристик сложной системы предлагается проведение аналогий между процессами, относящимися к различным областям науки. В частности, в резистивной модели сердечно-сосудистой системы за аналог сердца принимался источник несинусоидального переменного электрического напряжения, связанный с выпрямителем тока, представляющим собой сердечный клапан. А в модели электрической активности сердца для моделирования электрической активности возбудимых волокон сердца использовано приближение в виде генератора переменного электрического поля. Причем в последнем случае электрическое поле сердца представляется как поле точечного токового диполя с дипольным моментом вектора электрической напряженности, иначе называемого электрическим вектором сердца [6]. Известны также и другие модели сердца, основанные на анализе электрического поля, создаваемого сердцем, потенциалы которого затем регистрируются в различных точках [7]. Предложенные модели электрической активности сердца легли в основу разработки экспериментальных методов анализа сердечной деятельности по результатам регистрации разности электрических потенциалов с последующим анализом электрокардиограммы для оценки процессов жизнедеятельности органов и систем организма человека. Однако для решения задачи по определению топологии миокарда метрология электрических полей, наряду с традиционными задачами оценки значений потенциалов на поверхности кожных покровов, должна включать в себя задачу исследования неоднородного распределения поля. Последнее, применительно к регистрации электрических потенциалов, существенно затруднено как необходимостью инвазивной установки электродов на заданную глубину, так и тем, что при установке электродов вне кожных покровов результаты измерения трудно поддаются описанию ввиду существенных изменений диэлектрической проницаемости токопроводящих тканей как внутри тела, так и диэлектрической среды вне его, т.к. высокая, более 103, разность электрических сопротивлений кожных покровов и воздуха существенно затрудняет решение задачи определения внутренней структуры источника (топологии миокарда) по внешнему электрическому полю.
Известно, что электрические и магнитные поля взаимосвязаны [1] и всякое изменение электрического поля во времени 
вызывает в той же точке вихрь поля магнитного 
. Таким образом, согласно первому уравнению Максвелла, если в каждый данный момент деятельности сердца его дипольный электрический генератор создает вокруг электрическое поле (рис. 1), то одновременно возникает эквипотенциальное магнитное поле, качественные и количественные характеристики которого могут быть визуализированы.
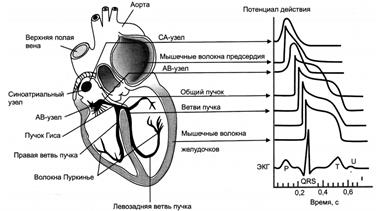
Рис. 1. Электрические потенциалы различных отделов сердца, формирующие электрокардиограмму [3]
Учитывая, что магнитная проницаемость в тканях тела человека и в окружающем пространстве отличается незначительно, то можно полагать, что метрология магнитного поля может оказаться более предпочтительной для решения задачи по «визуализации» топологии Мебиуса структуры миокарда сердца. Это делает актуальным построение математической модели, описывающей распространение магнитного поля, при изменении геометрических параметров магнитопровода, в частности его трансформации в форме петли Мебиуса.
Материалы и методы исследования
По аналогии с известной дипольной моделью сердца [3] на основании взаимосвязи электрического и магнитного полей принимаем, что имеется несколько магнитов, расположенных так, что расстояния между ними велики по сравнению с их размерами. В этом приближении можно считать, что конфигурация поля будет похожа на картину поля, создаваемую электрическими диполями [5]. Предположим, что эти магнитные диполи образованы фиктивными магнитными зарядами ±mi, расстояния между которыми li. Известно, что одиночный магнитный диполь создает магнитное поле, аналогичное полю электрического диполя [1]. Магнитостатическое взаимодействие отдельных компонентов внутри объема намагниченного тела приводит к возникновению собственной магнитостатической энергии этого тела, величина которого может быть определена как
, (1)
где Фi – магнитный потенциал, создаваемый всеми зарядами кроме i-го в месте расположения i-го заряда. Если принять, что магнитные заряды распределены в пространстве с плотностью 
, тогда выражение (1) удобно записать
, (2)
где V – объем магнетика.
Перепишем выражение (2) в соответствии с известными рекомендациями [2]:
. (2а)
Видно, что для пространства, заполненного магнитным материалом с намагниченностью JS , магнитостатическое взаимодействие отдельных элементов объема внутри намагниченного тела приводит к наличию собственной магнитостатической энергии этого тела, и величина поля рассеяния Hm ведет к образованию областей самопроизвольного намагничивания, т.е. доменной структуры. Это позволяет принять миокард сердца как магнитную доменную структуру – совокупность областей в магнитной подсистеме магнитных материалов, которые связывают микроскопические магнитные характеристики с их макроскопическими свойствами. Таким образом, при моделировании магнитного поля будем считать, что процессы намагничивания и перемагничивания определяются свойствами доменной структуры. Оценим влияние доменной структуры на распространение магнитного поля. Известно, что меридиан сердца [3] представляет собой тор с поверхностью Мебиуса. Для оценки влияния неориентированной поверхности на распространение в ее объеме магнитного поля принимаем энергию анизотропии и обменных взаимодействий пренебрежимо малыми. Также пренебрегаем шириной доменных границ. С учетом сделанных упрощений в расчетной модели принимаем, что магнитопровод (рис. 2, поз. 1) выполнен из ферромагнитного материала в виде тора с поверхностью Мебиуса и локальным расположением катушки намагничивания (рис. 2, поз. 2).
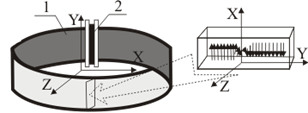
Рис. 2. Модель магнитопровода
Известно, что ферримагнитные тела состоят из областей самопроизвольного намагничивания, векторы намагниченности которых направлены в различные стороны, причем система в целом будет обладать минимумом энергии, если области будут намагничены антипараллельно. Однако если при решении задачи визуализации внутренней структуры миокарда сердца ферромагнитное тело поместить во внешнее магнитное поле, то под действием этого поля векторы намагниченности становятся параллельны [1]. Поэтому в модели принимаем, что векторы намагниченности направлены в одну сторону и «механически» меняют свое направление при прохождении «зоны Мебиусной закрутки».
С учетом сделанных допущений и упрощений выполним анализ распространения магнитного поля в торроидальном магнитопроводе с топологией Мебиуса и традиционном торроидальном исполнении. В расчетах принимали, что магнитопровод выполнен из ферромагнитного материала типа Magnifer с габаритными размерами: внутренний радиус 40 мм, внешний радиус 50 мм, сечение прямоугольное 10 мм. Ток частотой 50 Гц и силой до 1 А, вызывающий МДС, протекает через катушку с числом витков 100 (рис. 2).
Принимаем, что напряженность магнитного поля задается параметрами тока, текущего через катушку (рис. 2):
, (3)
где h – ширина магнитопровода; I – сила тока, текущего через катушку; w – число витков.
Тогда распределение магнитного поля по сечению удобно определить относительно средней линии магнитопровода:
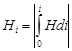, (4)
где i – шаг по сечению магнитопровода 
.
Распределение магнитной индукции по сечению, соответственно:
, (5)
где В – магнитная индукция, 
– магнитная постоянная составляющая, 
– магнитная проницаемость:
,
где S – площадь сечения магнитопровода; L – индуктивность.
Результаты расчета, демонстрирующие распространение магнитного поля по сечению магнитопровода и зависимость максимального значения напряженности от силы тока, приведены на рис. 3, 4. Видно, что напряженность поля по средней линии магнитопровода много меньше напряженности поля на его поверхности (рис. 3). Неравномерный характер распределения электромагнитной волны качественно соответствует известным представлениям [1] и связан с возникновением магнитного поверхностного эффекта, вызванного затуханием электромагнитной волны. Также видно, что с ростом силы тока, текущего через катушку (рис. 4), напряженность магнитного поля нелинейно возрастает и на принятом расчетном интервале силы тока до 0,1 А находится на начальном нелинейном участке, что делает значимым влияние потерь в магнитопроводе.
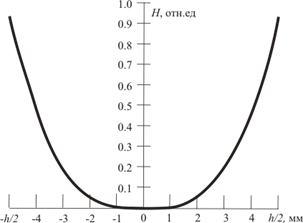
Рис. 3. Распространение электромагнитной волны по сечению магнитопровода
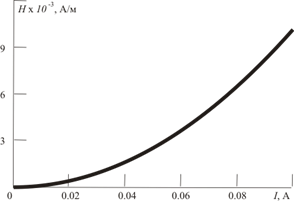
Рис. 4. График изменения максимального значения H от силы тока I
Пренебрегая потерями на вихревые токи, будем считать, что при периодическом намагничивании ферромагнитного материала потери в сердечнике обусловлены потерями на гистерезис. Оценим влияние гистерезиса методом Релея [10]. Для оценки уровня потерь на гистерезис определим намагничиваемость
, (6)
где c - магнитная восприимчивость, Hmax – наибольшее значение напряженности, достигаемое в материале сердечника (рис. 4).
Тогда магнитная индукция определяется:
, (7)
где Km – коэффициент намагничиваемости материала сердечника, принимаем, в соответствии с рекомендациями [8], равным 8.
Будем считать, что физические потери на гистерезис обусловлены доменной структурой магнитопровода (рис. 2). Также следует отметить, что значительно большая напряженность поля на периферии магнитопровода, по сравнению с его средней плоскостью, показывает необходимость оценить, как влияет при закручивании магнитопровода в петлю Мебиуса переход внутреннего диаметра во внешний и наоборот. Описание поверхности тора в традиционном исполнении и с поверхностью Мебиуса выполним по аналогии с описанием геометрии зацепления кольцевых винтовых передач 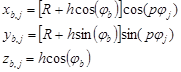[8]:
, (8)
где x, y, z - проекция на координаты (рис. 2); b, j – индексы дискретизации по осям х, y соответственно; R, r – внешний и внутренний радиус соответственно; φb, φj – углы закручивания в направлении осей х, y соответственно; p – шаг
.
При скручивании тора в поверхность Мебиуса деформация доменов происходит в плоскости xy. Тогда, полагая, что домены ориентированы в плоскости xy в направлении периферии, можно записать:
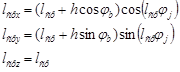, (9)
где lср – длина средней линии магнитопровода; lсрx, lсрy, lсрz – проекция средней линии магнитопровода на оси х, y, z соответственно.
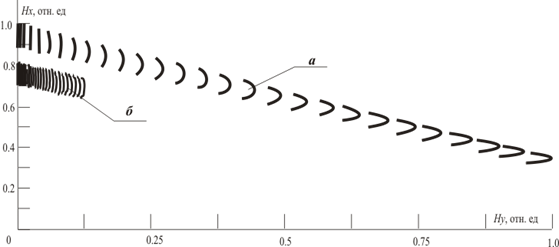
Рис. 5. Линии уровня напряженности магнитного поля в плоскости x, y:
Hx, Hy – проекция напряженности магнитного поля в плоскости х и y соответственно.
а – магнитопровод выполнен в виде тора, б – магнитопровод в форме петли Мебиуса
Результаты расчета (9), показывающие распределение напряженности в плоскости x, y, приведены с шагом 
(где n – переменная 1, 2…30) на рис. 5. Видно, что напряженность магнитного поля в магнитопроводе, выполненном в традиционной топологии (рис. 5а), больше, чем напряженность магнитного поля в магнитопроводе с топологией Мебиуса (рис. 5б). Причем в проекции оси х разница напряженностей составляет 25%, а в проекции оси у - достигает 10 раз, изменяясь с 0,1 до 1,0 отн. ед. Также отметим, что во всех случаях форма зависимости H качественно совпадает с формой распространения электромагнитной волны по сечению магнитопровода (рис. 3), что качественно подтверждает достоверность предложенной модели.
Заключение
В работе предложена математическая модель, описывающая влияние топологии Мебиуса на распространение магнитного поля в магнитопроводе. В приближении работы на участке начального намагничивания показана возможность изменения на порядок напряженности магнитного поля при изменении топологии магнитопровода. Причем в случае топологии Мебиуса напряженность уменьшается практически на порядок.
Работа выполнена при поддержке гранта РФФИ № 14-07-00468.
Рецензенты:
Черняев А.П., д.ф.-м.н., профессор, профессор кафедры высшей математики Московского физико-технического института (государственного университета), г. Москва;
Амасьянц Р.А., д.м.н., врач-невролог ООО «Сеть медицинских клиник «МедиАрт», г. Москва;
Пятакович Ф.А., д.м.н., профессор кафедры пропедевтики и внутренних болезней и клинических инфекционных технологий, Белгородский национальный исследовательский университет, г. Белгород.