В целях более эффективного отбора выпускников для продолжения образования в высших учебных заведениях с различными требованиями к уровню математической подготовки выпускников задания части 2 работы ЕГЭ по математике профильного уровня предназначены для проверки знаний на том уровне требований, которые традиционно предъявляются вузами с профильным экзаменом по математике [7].
Методический анализ предметных результатов ЕГЭ 2015 года по математике [3] позволяет выявить погрешности в развернутых решениях математических задач, допускаемые участниками в Алтайском крае, спроектировать предупреждающие и корректирующие действия по преодолению ошибок, в первую очередь, типичных.
В профильном ЕГЭ 2015 года модель задачи 15 (ранее – задача С1) не претерпела никаких изменений по сравнению с прошлым годом. Уже традиционно это была задача, состоящая из двух пунктов: решить тригонометрическое уравнение и отобрать корни уравнения из указанного промежутка.
Задача 15 ЕГЭ (профильный уровень) в 2015 году предполагала умение учащихся решать уравнения [4, 5, 6]. А именно:
– знание основных тригонометрических формул (основное тригонометрическое тождество);
– владение методом замены переменной при решении уравнения;
– умение решать квадратные уравнения;
– вычислительные навыки работы с числовыми иррациональными выражениями;
– умение решать простейшие тригонометрические уравнения по общим и частным формулам;
– знание области значений тригонометрических функций;
– владение хотя бы одним из способов отбора корней тригонометрического уравнения из указанного промежутка: с помощью единичной окружности, решением двойного неравенства, перебором, с помощью графика функции.
Приведем один из примеров задачи 15:
а) Решите уравнение: ![]() .
.
б) Укажите корни этого уравнения, принадлежащие отрезку ![]() .
.
Задача оценивалась экспертами ЕГЭ:
– 2 баллами при обоснованном решении обоих пунктов;
– 1 баллом при обоснованном решении одного из пунктов задачи или если получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов;
– 0 баллов во всех остальных случаях [1].
На рисунке наглядно представлены результаты выполнения задания 15 экзаменационной работы ЕГЭ (профильный уровень) учащимися Алтайского края в 2015 года в первичных баллах.
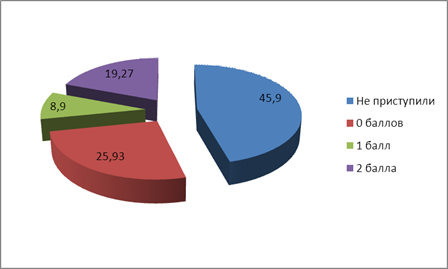
Результаты выполнения задания 15 в первичных баллах
Вообще, процент учащихся, получивших положительный балл (1 или 2) за решение задачи 15, в Алтайском крае в 2015 году находится в норме (10–50 %) и составляет 28,17 %. Однако можно выделить ряд типичных ошибок участников экзамена при выполнении данного задания.
1. Одной из самых распространенных ошибок при решении задачи 15 в 2015 году были неточности и заблуждения в формулах корней простейших тригонометрических уравнений: использование формулы корней для простейшего тригонометрического уравнения относительно синуса – к уравнению относительно косинуса и, наоборот, неверная периодичность корней, описки и другие ошибки в записи корня. Эти ошибки приводили к тому, что решения уравнения указывались неверно, и как следствие – первый пункт задачи не был выполнен.
Например, при решении простейшего тригонометрического уравнения относительно синуса ![]() учащиеся приводили:
учащиеся приводили:
а) неверное решение ![]() ,
, ![]() , ошибочно используя формулу для корней простейшего тригонометрического уравнения относительно косинуса;
, ошибочно используя формулу для корней простейшего тригонометрического уравнения относительно косинуса;
б) неверное решение ![]() ,
, ![]() вместо верного решения
вместо верного решения ![]() ,
, ![]() .
.
2. Не менее редкой ошибкой при решении задачи 15 в 2015 году было неверное вычисление значения обратной тригонометрической функции: либо неверные значения аркфункций, либо неверное преобразование аркфункций отрицательного аргумента. Эти ошибки также приводили к тому, что корни уравнения указывались неверно, и как следствие – первый пункт задачи не был выполнен.
Например, при решении простейшего тригонометрического уравнения ![]() , учащиеся допускали типичную ошибку:
, учащиеся допускали типичную ошибку: 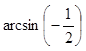 считали равным
считали равным ![]() , а не
, а не ![]() .
.
Кроме того, часто учащиеся считали, что ![]() вместо верного
вместо верного ![]() . Возможно перенося свойство четности функции
. Возможно перенося свойство четности функции ![]() на функцию
на функцию ![]() .
.
3. Достаточно много ошибок было связано с незнанием множества значений тригонометрических функций синус и косинус. Учащиеся записывали формулу корней тригонометрических уравнений ![]() или
или ![]() не принимая во внимание условие
не принимая во внимание условие ![]() , при котором эти уравнения вообще имеют решения.
, при котором эти уравнения вообще имеют решения.
Например, в работах учащихся довольно часто в формуле корней тригонометрического уравнения встречались несуществующие значения обратных тригонометрических функций: ![]() (не замечая, что
(не замечая, что ![]() ) и др.
) и др.
4. К типичным ошибкам при решении задачи 15 можно отнести потерю корней при переходе от решения простейшего тригонометрического уравнения в общем виде к частному виду.
Например, записав верное решение 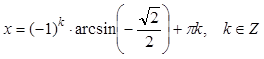 уравнения
уравнения ![]() , упрощая выражение в правой части равенства, учащиеся допускали ошибку: например, записывая
, упрощая выражение в правой части равенства, учащиеся допускали ошибку: например, записывая ![]() . Последняя формула задает совсем не те значения, которые задает первая формула. В итоге – в ответе пункта а) записано неверное решение.
. Последняя формула задает совсем не те значения, которые задает первая формула. В итоге – в ответе пункта а) записано неверное решение.
5. Нарушение логики умозаключений, отсутствие логических связок, рассмотрение одного частного случая верного равенства вместо решения задачи
Например, от уравнения вида «сумма равна нулю» учащиеся довольно часто переходили к системе уравнений, в которой приравнивали к нулю каждое слагаемое. При этом, делая ошибочное заключение «сумма равно нулю тогда и только тогда, когда каждое слагаемое равно нулю». Среди работ 2015 года ошибка такого рода приобрела популярность. Учащиеся сводили глобальное решение уравнения к исследованию одного частного случая. Причем, размышления чаще всего проводились без логических связок «и» или «или».
6. Неточности и описки при решении тригонометрического уравнения или отборе корней уравнения из указанного промежутка
7. Нехарактерная в прошлых годах для задачи такого типа ошибка – неумение работать с иррациональными числовыми выражениями. В связи с этим для многих учащихся решение квадратного уравнения с иррациональными коэффициентами представляло трудность (чаще всего решение не доводилось до конца).
Например, получив (после замены тригонометрической функции на t) квадратное уравнение ![]() , многие учащиеся испытывали затруднения даже при вычислении дискриминанта (по причине иррациональности коэффициентов). Некоторые учащиеся, все-таки вычислив дискриминант и получив
, многие учащиеся испытывали затруднения даже при вычислении дискриминанта (по причине иррациональности коэффициентов). Некоторые учащиеся, все-таки вычислив дискриминант и получив ![]() , не провели преобразование
, не провели преобразование ![]() . Это сделало корни уравнения громоздкими
. Это сделало корни уравнения громоздкими ![]() и в основном приводило решение в тупик.
и в основном приводило решение в тупик.
8. По-прежнему, как и в прошлых годах, учащиеся теряют баллы в пункте б) решения задачи 15 по причине отсутствия обоснования отбора корней из промежутка. 1 балл за решение пункта б) выставляется при условии присутствия «следов» отбора корней, что зачастую не имело места в работах участников экзамена 2015 года.
Следует отметить, что по сравнению с 2014 годом при решении задачи 15 улучшилась ситуация с обоснованным отбором корней их промежутка. Учащиеся активно использовали различные способы отбора корней:
1. Арифметический способ:
а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;
б) перебор значений целочисленного параметра и вычисление корней.
2. Алгебраический способ:
а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней;
б) исследование уравнения с двумя целочисленными параметрами.
3. Геометрический способ:
а) изображение корней на тригонометрической окружности с последующим отбором и учетом имеющихся ограничений;
б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.
4. Функционально-графический способ:
выбор корней с помощью графика простейшей тригонометрической функции.
В основном учащиеся успешно проводили отбор корней, принадлежащих промежутку.
Таким образом, на основе анализа типичных ошибок в решениях задачи 15 участников ЕГЭ по математике в 2015 году среди причин их появления можно выделить: незнание основных формул корней простейших тригонометрических уравнений, табличных значений тригонометрических функций; невладение понятием множества значений тригонометрической функции, недостаточно развитые вычислительные навыки и навыки тождественных преобразований.
Для предупреждения этих ошибок, в узком смысле, необходимо при изучении раздела «Тригонометрия» в основной и старшей школе добиваться от учащихся абсолютного знания всех основных теоретических сведений этого раздела, так как это служит основой успешного преобразования тригонометрического выражения, решения тригонометрического уравнения и неравенства, присутствующих в КИМах профильного ЕГЭ по математике.
В широком смысле, необходимо обеспечить тенденцию повышения качества результатов ЕГЭ с применением комплекса мер, в первую очередь организационно-методического и методического характера, по выявлению потенциальных погрешностей в решении задач 15 профильного уровня будущими участниками экзамена 2016 г. и осуществлению соответствующих корректирующих мероприятий.
Для учащихся с разным уровнем подготовки должны быть выстроены принципиально разные стратегии подготовки к профильному экзамену, необходима дифференциация обучения, разработка стратегии обучения и подготовки к выпускному экзамену с учетом уже имеющегося у выпускника уровня образовательной подготовки. Прежде всего, учителю необходимо познакомиться со структурой и содержанием КИМов, сравнить их с содержанием программного материала и того учебника, по которому учатся школьники. Целесообразно организовать еще и индивидуальное повторение, учитывающее пробелы в знаниях и умениях конкретного ученика, и с помощью диагностических работ систематически фиксировать продвижение старшеклассника по пути достижения уровня запланированных требований.
При новой форме диагностики качества образования учителю необходимо непрерывно повышать свой профессиональный академический уровень [2]. Если раньше (до ЕГЭ) учитель считал, что подготовка выпускников к поступлению в вуз не является его задачей и задачей школы, что учитель не несет ответственности за поступление или не поступление в вуз, то сейчас каждый учитель (как основной, так и старшей школы) заинтересован в получении высоких результатов ЕГЭ, так как по ним могут судить о его профессионально-академическом уровне. В этом смысле задача 15 (повышенного уровня сложности) профильного ЕГЭ по математике является перспективной в силу своей доступности учащимся со средним и хорошим уровнем подготовки по предмету.
Результаты ЕГЭ по математике пройдут обсуждение на методических объединениях учителей математике г. Барнаула и педагогических советах в 2015–2016 году.
Для повышения качества подготовки учащихся к Единому государственному экзамену профильного уровня подобный анализ целесообразно проводить для всех задач с развернутым ответом, прогнозировать пути предупреждения типичных ошибок участников экзамена.
Рецензенты:
Овчаров А.В., д.п.н., профессор, директор института физико-математического образования ФГБОУ ВО «Алтайский государственный педагогический университет» Министерства науки и образования РФ, г. Барнаул;
Пышнограй Г.В., д.ф.-м.н., профессор, заведующий кафедрой математического анализа и прикладной математики, ФГБОУ ВО «Алтайский государственный педагогический университет» Министерства науки и образования РФ, г. Барнаул.



