В работах Е.М. Минского, А.Л. Хейна, Г.А. Зотова, С.М. Тверковкина, З.С. Алиева и иных[1] рассматривалась данная задача в приближенной постановке. Здесь рассматривается задача о притоке реального газа к несовершенной скважине в однородно-анизотропном пласте в более строгой постановке, т.е. с учетом анизотропии, на основе теории потенциала, а также предлагается несколько иной подход к расчету фильтрационных сопротивлений, обусловленных несовершенством скважины по степени вскрытия и нелинейным законом фильтрации.
В связи с этим к выводу уравнения притока газа можно подойти следующим образом. Для нелинейного закона фильтрации Е.М. Минским и И.А. Чарным предложено уравнение:
![]() (1)
(1)
где ν – скорость фильтрации; ρг – плотность газа; l – коэффициент макрошероховатости [2].
Геометрия потока, очевидно, будет определяться функцией h=h(r) в области пространственного движения rc≤r≤Ro (рис. 1). Вся трудность решения состоит в нахождении уравнения кривой h=h(r), ограничивающей область потока, или, другими словами, уравнения линии тока. Размер зоны пространственного движения будет зависеть от многих факторов (например, не только от геометрии пласта (Rk,ho,b), но и от анизотропии пласта æ*, дебита, Q, градиента давления (gradP) и т.д.). И.А. Чарный [3] и М. Маскет [4] предлагают принимать радиус зоны пространственного притока Ro=ho. Будем аппроксимировать упомянутую линию тока уравнением вида [2]:
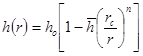 , (2)
, (2)
где ![]() – некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта.
– некоторая функция, зависящая от несовершенства скважины по степени вскрытия, геометрии пласта и скважины, анизотропии пласта.
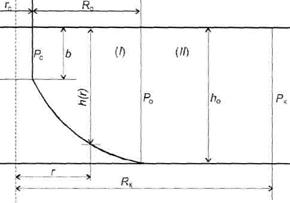
Рис. 1. Двухзонная схема притока к несовершенной скважине, обусловленного нелинейным законом фильтрации
Умножая левую и правую части уравнения (1) на ρг(P), применяя двухзонную схему притока и принимая размер зоны пространственного притока Ro=ho, учитывая уравнение состояния реального газа, вводя добавочные фильтрационные сопротивления С1, С2 и Со, обусловленные относительным вскрытием, нарушением линейного закона Дарси и перфорацией колонны, и интегрируя в соответствующих пределах по давлению и радиусу, после некоторых преобразований получаем известную двучленную формулу притока:
![]() (3)
(3)
где
 ;
; ![]() (4)
(4)
![]()
![]()
![]() ;
; ![]() (5)
(5)
![]() ;
; ![]() (6)
(6)
![]() ;
; ![]() ;
; ![]() ;
; 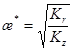 (7)
(7)
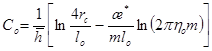 (8)
(8)
Обозначения в формулах общепринятые.
Для внешней зоны двучленная формула записывается как приток к «укрупненной» скважине радиуса Ro=ho (см. рис. 1):
![]() (9)
(9)
где
![]()
![]() (10)
(10)
Решая совместно (3) и (9) с учетом (4), и (10), получаем уравнения притока, характеризующие всю область дренирования:
![]() (11)
(11)
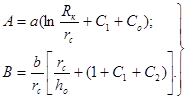 (12)
(12)
Значения добавочных фильтрационных сопротивлений определяются по таблицам и графикам [5].
Для определения предельной депрессии по формуле (11) необходимо знать предельный безводный дебит Qпр газовой скважины при нелинейном законе фильтрации. Решение этой задачи связано с распределением потенциала в случае притока реального газа к несовершенной скважине. Такое решение пока не получено.
Используем уравнение для распределения потенциала скорости фильтрации Ф при линейном законе в случае притока несжимаемой жидкости к несовершенной скважине [6, 7]:
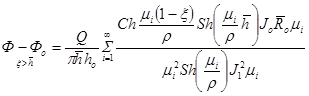 , (13)
, (13)
где
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; 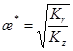 (14)
(14)
где Q – расход жидкости; ho – продуктивная толщина пласта; ![]() – относительное вскрытие пласта;
– относительное вскрытие пласта; ![]() положительный корень уравнения Jo(
положительный корень уравнения Jo(![]() )=0; Jo(x) – функция Бесселя первого рода нулевого порядка; J1(x) – функция Бесселя первого рода первого порядка; Sh(x) и Ch(x) – гиперболический синус и косинус; Ro – радиус контура питания; æ* – анизотропия пласта; Фо – потенциал на контуре питания; Ф – потенциал в любой точке пласта.
)=0; Jo(x) – функция Бесселя первого рода нулевого порядка; J1(x) – функция Бесселя первого рода первого порядка; Sh(x) и Ch(x) – гиперболический синус и косинус; Ro – радиус контура питания; æ* – анизотропия пласта; Фо – потенциал на контуре питания; Ф – потенциал в любой точке пласта.
Преобразуем уравнение (13) для притока газа путем замены объемного расхода Q на весовой G и давления Р на функцию Лейбензона:
![]() (15)
(15)
Используя уравнение газового состояния:
![]() ;
; ![]() (16)
(16)
интегрируя (15), обозначая сумму ряда уравнений (13) при ![]() через функцию
через функцию ![]() , переходя от потенциала к давлению и решая совместно (13) и (15), получаем при
, переходя от потенциала к давлению и решая совместно (13) и (15), получаем при![]() :
:
![]() (17)
(17)
Условие устойчивости конуса подошвенной воды определяется по закону Паскаля [2, 6]:
![]() ;
; ![]() (18)
(18)
Пусть предельная высота вершины конуса (см. рис.) определяется ординатой ![]() =
=![]() . Тогда, решая совместно (17) и (18), после ряда преобразований получим формулу для безразмерного предельного дебита газовой скважины:
. Тогда, решая совместно (17) и (18), после ряда преобразований получим формулу для безразмерного предельного дебита газовой скважины:
![]() , (19)
, (19)
где
![]() ;
;![]() (20)
(20)
![]() (21)
(21)
Здесь ![]() – функция безразмерного предельного дебита по жидкости рассчитана на ЭВМ в широком диапазоне параметров ξo, ρ и
– функция безразмерного предельного дебита по жидкости рассчитана на ЭВМ в широком диапазоне параметров ξo, ρ и ![]() , затабулирована и представлена графическими зависимостями [6, 8, 9]; Po – начальное средневзвешенное пластовое давление газовой залежи;
, затабулирована и представлена графическими зависимостями [6, 8, 9]; Po – начальное средневзвешенное пластовое давление газовой залежи; ![]() – ордината вершины устойчивого конуса воды.
– ордината вершины устойчивого конуса воды.
Из соотношения (19) следует формула для предельного безводного расхода газа:
![]() (22)
(22)
Параметр m определяет термодинамический характер расширения газа при фильтрации его из области высокого давления в область пониженного [3]. При m=1 происходит изотермическое расширение газа. В случае адиабатического расширения ![]() (Сv и Cp – удельные теплоемкости газа при постоянном объеме и давлении соответственно).
(Сv и Cp – удельные теплоемкости газа при постоянном объеме и давлении соответственно).
Следует заметить, что предельный безводный дебит ![]() , формула (20), рассчитывается в широком диапазоне параметров
, формула (20), рассчитывается в широком диапазоне параметров ![]() и
и ![]() по всему удельному объему дренирования [6,8], где Ro – условный радиус контура питания, составляющий половину расстояния между скважинами. Однако можно получить наиболее строгое решение исходя из двухзонной схемы притока (см. рис.).
по всему удельному объему дренирования [6,8], где Ro – условный радиус контура питания, составляющий половину расстояния между скважинами. Однако можно получить наиболее строгое решение исходя из двухзонной схемы притока (см. рис.).
Для внутренней зоны радиуса Ro=ho согласно (13) при ξ=ξо имеем:
![]() . (23)
. (23)
Для внешней зоны в соответствии с притоком жидкости к укрупненной фиктивной скважине радиуса Ro=ho по формуле Дюпюи находим:
![]() . (24)
. (24)
Совместное решение приведенных уравнений дает:
![]() , (25)
, (25)
где ![]() – безразмерная ордината вершины конуса воды; zo – ордината вершины конуса воды;
– безразмерная ордината вершины конуса воды; zo – ордината вершины конуса воды; ![]() – параметр размещения Ro=ho.
– параметр размещения Ro=ho.
Состояние предельно устойчивого конуса выразим по уравнению Паскаля:
![]() . (26)
. (26)
Решая совместно (25) и (26), после ряда преобразований получаем:
![]() ;
; 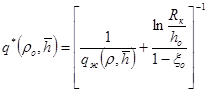 (27)
(27)
где Qo – определяется по формуле (21).
Для расчета предельного дебита газовой скважины следует в формуле (22) вместо ![]() принять
принять ![]() по формуле (27).
по формуле (27).
Выводы
1. На основе теории потенциала разработана методика определения предельных безводных дебитов и депрессий вертикальных газовых скважин в более строгой постановке задачи (использование двухзонной схемы притока, учет анизотропии пласта, средневзвешенного давления, добавочных фильтрационных сопротивлений).
2. Приведены практические расчеты.
Рецензенты:
Грачёв С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень;
Сохошко С.К., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень.



