В данной статье приводится аналитическое решение указанной задачи и рассмотрен случай, когда несовершенная скважина вскрыла однородно-анизотропный круговой пласт с подошвенной водой и эксплуатируется при наличии непроницаемого экрана (рисунок 1). Считаем, что газ реальный, движение газа, установившееся и подчиняется нелинейному закону фильтрации.
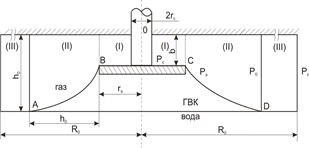
Рис.1. Трехзонная схема притока газа к несовершенной скважине с экраном
Исходя из принятых условий, уравнения притока газа к скважине в зонах I, II, III соответственно примут вид:
![]()
![]()
![]() ; (1)
; (1)
![]()
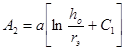 ;
; ![]() ; (2)
; (2)
![]() ;
; ![]() ;
; ![]() , (3)
, (3)
где a и b определяются по формулам. Остальные обозначения показаны на схеме (см. рисунок 1). Уравнения (2) и (3) в данном случае описывают приток к укрупненным скважинам соответственно с радиусами rэ и (rэ+ho).
Условие устойчивости на границе раздела газ-вода (см. линию СD) по закону Паскаля запишется уравнением [1,2]
![]() , (4)
, (4)
где ρв – плотность воды, ![]() – капиллярное давление как функция насыщенности водой на границе раздела газ-вода.
– капиллярное давление как функция насыщенности водой на границе раздела газ-вода.
Решая совместно (1)-(3), после ряда преобразований, получаем уравнение притока
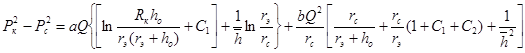 . (5)
. (5)
Из совместного решения (2) и (4) получаем квадратное уравнение относительно безразмерного предельного дебита ![]() , один из корней которого с учетом (7) и после ряда преобразований представляется выражением:
, один из корней которого с учетом (7) и после ряда преобразований представляется выражением:
![]()
![]()
![]() ;
; ![]() (6)
(6)
где 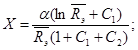
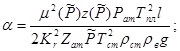 (7)
(7)
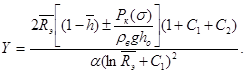 (8)
(8)
Переход к размерному предельному безводному дебиту осуществляется по формулам:
![]()
![]() (9)
(9)
где ![]() – средневзвешенное давление в газовой залежи.
– средневзвешенное давление в газовой залежи.
Таблица 1
Значения фильтрационных сопротивлений, обусловленных экраном на забое
|
Rэ |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
10,0 |
20,0 |
|||||||
|
|
С1 |
С2 |
С1 |
С2 |
С1 |
С2 |
С1 |
С2 |
С1 |
С2 |
С1 |
С2 |
С1 |
С2 |
|
ρо=0,1 |
||||||||||||||
|
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 |
2,20 1,10 0,60 0,40 0,15 0,10 - - - |
37,0 12,4 3,0 1,4 0,8 0,5 0,3 0,1 - |
4,70 2,30 1,30 0,80 0,40 0,15 0,10
- |
46,0 14,8 5,2 2,4 1,6 0,8 0,3 0,1 - |
6,8 3,4 2,0 1,2 0,6 0,4 0,2 0,2 - |
50,40 16,20 6,40 4,20 2,80 1,00 0,45 0,20 0,10 |
8,70 4,30 2,50 1,50 0,80 0,60 0,40 0,11 - |
55,40 17,20 7,00 3,50 2,00 1,20 0,50 0,22 0,10 |
10,30 5,20 3,00 1,80 1,00 0,80 0,40 0,11 - |
62,1 17,3 7,6 3,7 2,1 1,6 0,6 0,3 0,1 |
17,17 8,32 4,98 3,23 2,16 1,44 0,91 0,52 0,21 |
71,64 19,28 8,34 4,34 2,46 1,42 0,78 0,37 0,10 |
21,41 11,09 6,59 4,27 2,85 1,90 1,21 0,69 0,29 |
81,37 21,16 9,08 4,74 2,70 1,58 0,90 0,46 0,16 |
|
ρо=0,5 |
||||||||||||||
|
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 |
0,30 0,23 0,20 0,15 0,10 - - - - |
3,30 1,20 0,80 0,60 0,40 0,20 0,10 - - |
0,60 0,45 0,39 0,27 0,20 0,10 - - - |
6,8 12,4 1,5 1,0 0,6 0,3 0,2 0,1 - |
0,90 0,70 0,59 0,46 0,28 0,15 0,12 - - |
10,2 3,6 2,2 1,3 0,8 0,4 0,2 0,1 - |
1,25 0,90 0,75 0,55 0,40 0,25 0,15 - - |
13,80 4,80 2,80 1,70 1,00 0,50 0,25 0,10 - |
1,60 1,15 0,95 0,75 0,50 0,29 0,18 0,11 - |
17,00 6,0 3,40 2,0 1,20 0,60 0,30 0,15 0,10 |
7,08 4,54 3,34 2,28 1,55 1,02 0,61 0,31 0,10 |
27,65 11,39 5,71 3,18 1,85 1,06 0,56 0,23 0,10 |
13,32 7,71 4,96 3,32 2,24 1,48 0,91 0,48 0,16 |
46,59 15,21 7,14 3,89 2,95 1,32 0,74 0,36 0,10 |
|
ρо=1,0 |
||||||||||||||
|
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 |
0,30 0,25 0,20 0,15 0,10 - - - |
1,30 0,60 0,30 0,20 0,10 - - - |
0,62 0,46 0,38 0,30 0,20 0,10 - - |
2,5 1,2 0,7 0,4 0,2 0,1 - - |
0,95 0,70 0,51 0,46 0,28 0,18 0,10 - |
4,00 1,70 1,00 0,60 0,35 0,20 0,10 - |
1,25 0,92 0,75 0,60 0,40 0,25 0,15 0,10 |
5,10 2,30 1,40 0,80 0,50 0,30 0,17 0,10 |
1,55 1,15 0,97 0,75 0,48 0,30 0,18 0,10 |
6,60 2,55 1,80 1,15 0,60 0,35 0,20 0,10 |
3,14 2,28 1,89 1,37 0,95 0,61 0,35 0,10 |
13,20 5,77 3,45 2,06 1,23 0,70 0,38 0,10 |
7,38 5,16 3,51 2,41 1,64 1,07 0,65 0,32 |
26,38 10,67 5,39 3,04 1,80 1,06 0,59 0,27 |
Добавочные фильтрационные сопротивления ![]() и
и ![]() , обусловленные экраном, рассчитаны на ЭВМ по формулам (6), затабулированы (таблица 1) и представлены графиками (рисунок 2). Функция (6) рассчитана на ЭВМ и представлена графически при
, обусловленные экраном, рассчитаны на ЭВМ по формулам (6), затабулированы (таблица 1) и представлены графиками (рисунок 2). Функция (6) рассчитана на ЭВМ и представлена графически при ![]() (рисунок 3). Предельная депрессия
(рисунок 3). Предельная депрессия ![]() может быть установлена по уравнению притока (4.4.4) при
может быть установлена по уравнению притока (4.4.4) при ![]() Q=Qпр.
Q=Qпр.
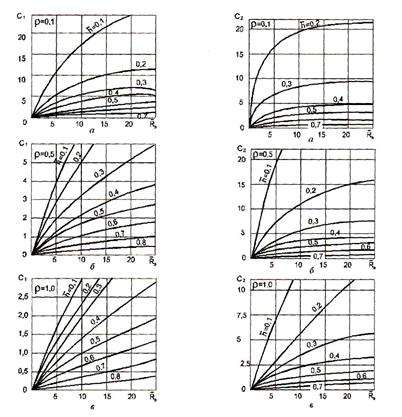
Рис.2. Фильтрационные сопротивления ![]() и
и ![]() , обусловленные экраном при устойчивой границе раздела газ-вода
, обусловленные экраном при устойчивой границе раздела газ-вода
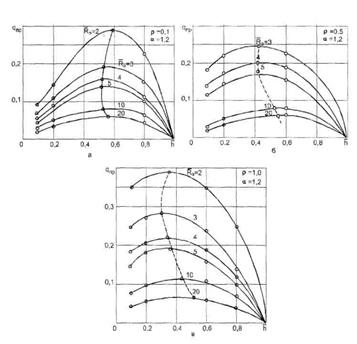
Рис.3. Зависимость безразмерного предельного дебита qпр от относительного вскрытия ![]() при параметрах
при параметрах ![]() , ρ=1/æ* и α
, ρ=1/æ* и α
На рисунке 3 приведены зависимости безразмерного предельного дебита q от степени вскрытия ![]() при параметрах Rэ и α. Кривые показывают, что с увеличением размера экрана (
при параметрах Rэ и α. Кривые показывают, что с увеличением размера экрана (![]() <20) безводные дебиты увеличиваются. Максимум на кривых соответствует оптимальному вскрытию пласта, при котором можно получить наибольший предельный безводный дебит для заданного размера экрана. С увеличением параметра ρ=1/æ* (уменьшением анизотропии) предельный безводный дебит увеличивается, а уменьшение безводного дебита для малых вскрытий объясняется увеличением фильтрационных сопротивлений, обусловленных экраном на забое.
<20) безводные дебиты увеличиваются. Максимум на кривых соответствует оптимальному вскрытию пласта, при котором можно получить наибольший предельный безводный дебит для заданного размера экрана. С увеличением параметра ρ=1/æ* (уменьшением анизотропии) предельный безводный дебит увеличивается, а уменьшение безводного дебита для малых вскрытий объясняется увеличением фильтрационных сопротивлений, обусловленных экраном на забое.
Пример. Дренируется газовая шапка, контактирующая с подошвенной водой. Требуется определить: предельный дебит газовой скважины, ограничивающий прорыв ГВК к забою и предельный дебит при наличии непроницаемого экрана.
Исходные данные: Рпл=26,7 МПа; К=35,1·10-3 мкм2; Ro=300 м; ho=7,2 м; ![]() =0,3;
=0,3; ![]() =978 кг/м3;
=978 кг/м3; ![]() =210 кг/м3 (в пластовых условиях); æ*=6,88;
=210 кг/м3 (в пластовых условиях); æ*=6,88; ![]() =0,02265 МПа·с (в пластовых условиях); Тпл=346 К; Тст=293 К; Рат=0,1013 МПа; rэ=ho=7,2 м и rэ=0,5ho=3,6 м.
=0,02265 МПа·с (в пластовых условиях); Тпл=346 К; Тст=293 К; Рат=0,1013 МПа; rэ=ho=7,2 м и rэ=0,5ho=3,6 м.
Определяем параметр размещения
![]()
Из графиков [2,3,4] находим безразмерный предельный безводный дебит жидкости q(ρо,![]() )q(6,1;0,3)=0,15.
)q(6,1;0,3)=0,15.
По формуле (9) подсчитываем:
Qo=52,016 тыс. м3/сут; ![]() тыс. м3/сут.
тыс. м3/сут.
Определяем безразмерные параметры при наличии экрана:
![]()
![]()
![]()
По графикам (см. рисунок 2) или таблице находим добавочные фильтрационные сопротивления: С1![]() = С1(0,15;0,3;1)=0,6; С2
= С1(0,15;0,3;1)=0,6; С2![]() = С2(0,15;0,3;1)=3,0.
= С2(0,15;0,3;1)=3,0.
По формуле (7) находим безразмерный параметр α=394,75.
По формуле (9) подсчитываем дебит, который составил Qo![]() 47,9 тыс.м3/сут.
47,9 тыс.м3/сут.
Расчеты по формулам (7) и (8) дают: Х=51,489 и Y=5,773·10-2.
Безразмерный предельный дебит, рассчитанный по формуле (6), равен q![]() =1,465.
=1,465.
Определяем размерный предельный дебит, обусловленный экраном, из соотношения Qпр=q![]() Qo=1,465·47,9
Qo=1,465·47,9![]() 70,188 тыс.м3/сут.
70,188 тыс.м3/сут.
Расчетный предельный дебит без экрана с аналогичными исходными параметрами составляет 7,8 тыс. м3/сут. Таким образом, в рассматриваемом случае наличие экрана увеличивает предельный дебит почти в 10 раз.
Если принять rэ=3,6 м; т.е. в два раза меньше размеру, чем газонасыщенная толщина, тогда получаем следующие расчетные параметры:
![]() =2; С1=1,30; С2=5,20; Х=52,45; Y=1,703·10-2; q
=2; С1=1,30; С2=5,20; Х=52,45; Y=1,703·10-2; q![]() =0,445 и Qпр=21,3 тыс.м3/сут. В данном случае предельный дебит увеличивается всего лишь в 2,73 раза.
=0,445 и Qпр=21,3 тыс.м3/сут. В данном случае предельный дебит увеличивается всего лишь в 2,73 раза.
Следует отметить, что величина предельного дебита зависит не только от размеров экрана, но и от его положения по вертикали газонасыщенного пласта, т.е. от относительного вскрытия пласта ![]() , если экран располагается непосредственно перед забоем. Исследование решения (6) показало, что существует оптимальное положение
, если экран располагается непосредственно перед забоем. Исследование решения (6) показало, что существует оптимальное положение ![]() экрана, зависящее от параметров ρ, α, Rэ, которое соответствует наибольшему предельному дебиту. В рассмотренной задаче оптимальным вскрытием является
экрана, зависящее от параметров ρ, α, Rэ, которое соответствует наибольшему предельному дебиту. В рассмотренной задаче оптимальным вскрытием является ![]() =0,6.
=0,6.
Принимаем ρ=0,145 и ![]() =1. По изложенной методике получаем расчетные параметры: С1=0,1; С2=0,5; X=24,672; Y=0,478.
=1. По изложенной методике получаем расчетные параметры: С1=0,1; С2=0,5; X=24,672; Y=0,478.
Определяем безразмерный дебит:
q=24,672(![]() -1)
-1) ![]() 5,323.
5,323.
Размерный предельный дебит находится по формуле (9)
Qпр=qQo=5,323·103=254,94 тыс.м3/сут.
Таким образом, дебит по сравнению с относительным вскрытием ![]() =0,3 увеличился в 3,6 раза.
=0,3 увеличился в 3,6 раза.
Изложенный здесь способ определения предельного безводного дебита является приближенным, так как он рассматривает устойчивость конуса, вершина которого уже достигла радиуса экрана rэ.
При ![]() из приведенных решений получим формулы для определения q(
из приведенных решений получим формулы для определения q(![]() ) для несовершенной газовой скважины в условиях нелинейного закона фильтрации с учетом добавочных фильтрационных сопротивлений. Эти формулы также будут приближенными, и по ним рассчитывается завышенное значение предельного безводного дебита.
) для несовершенной газовой скважины в условиях нелинейного закона фильтрации с учетом добавочных фильтрационных сопротивлений. Эти формулы также будут приближенными, и по ним рассчитывается завышенное значение предельного безводного дебита.
Для построения двухчленного уравнения притока газа в условиях предельно-устойчивого конуса подошвенной воды необходимо знать фильтрационные сопротивления именно в этих условиях. Определить их можно исходя из теории устойчивого конусообразования Маскета-Чарного. Уравнение линии тока, ограничивающей область пространственного движения к несовершенной скважине в однородно-анизотропном пласте, когда уже произошел прорыв вершины конуса к забою скважины, в соответствии с теорией безнапорного движения, запишем в виде
![]() (10)
(10)
где q=![]() – безразмерный предельный безводный дебит, определяемый по приведенным (известным) приближенным формулам и графикам;
– безразмерный предельный безводный дебит, определяемый по приведенным (известным) приближенным формулам и графикам; ![]() – безразмерный параметр.
– безразмерный параметр.
Выражая скорость фильтрации через расход ![]() , подставляя уравнение границы раздела (10) в дифференциальное уравнение (1), учитывая закон газового состояния и интегрируя по давлению Р и радиусу r в соответствующих пределах, получим уравнение притока вида (12) и формулы (13), в которых следует принять:
, подставляя уравнение границы раздела (10) в дифференциальное уравнение (1), учитывая закон газового состояния и интегрируя по давлению Р и радиусу r в соответствующих пределах, получим уравнение притока вида (12) и формулы (13), в которых следует принять:
![]() ;
; ![]() , (11)
, (11)
![]() (12)
(12)
где Li(x) – интегральный логарифм, который связан с интегральной функцией зависимостью [5].
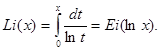 (13)
(13)
При x>1 интеграл (13) расходится в точке t=1. В этом случае под Li(x) надо понимать значение несобственного интеграла. Поскольку методы определения безразмерных предельных безводных дебитов хорошо известны, то, очевидно, нет необходимости табулировать функции (11) и (12).
Выводы
1. Разработана приближенная методика расчета предельных безводных дебитов вертикальных газовых скважин при нелинейном законе фильтрации, обусловленных наличием непроницаемого забойного экрана. Безразмерные предельные дебиты и соответствующие добавочные фильтрационные сопротивления рассчитаны на компьютере, результаты затабулированы и приведены соответствующие графические зависимости.
2. Установлено, что величина предельного безводного дебита зависит не только от размеров экрана, но и от его положения по вертикали газонасыщенного пласта; определено оптимальное положение экрана, характеризующее наибольшим предельным дебитом.
3. Произведены практические расчеты на конкретном примере.
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень;
Сохошко С.К., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень.



