Деформирование грунта при оттаивании изучено лишь для условий нагружения, близких к компрессионным. Единственной зависимостью, связывающей деформации оттаивания (относительную осадку S) с напряженным состоянием (внешним давлением Р), является известная формула Цытовича – Лапкина:
где А и 
– коэффициенты оттаивания и сжимаемости.
Однако во многих практически важных случаях компрессионной зависимости недостаточно для анализа напряженно-деформированного состояния оттаивающего основания автомобильной дороги. Так, если размеры в плане чаши протаивания заметно превосходят размеры загружаемого участка, то пренебрежение пространственными эффектами (рассеивание напряжений с глубиной, горизонтальные перемещения грунта по склону) недопустимо. На практике в этом случае зависимость “подправляют” коэффициентами, полученными из решения упругой задачи, что применительно к оттаивающему грунту не вполне корректно [1].
В данной работе приведены результаты экспериментальных исследований деформирования оттаивающего грунта при различных способах нагружения (в компрессионном приборе и стабилометре).
Испытывались серии из 3 – 5 идентичных образцов, промороженных под одной и той же (в пределах одной серии) нагрузкой 
и оттаенных затем в компрессионных опытах – под различными нагрузками, включая , в стабилометре – при различных сочетаниях вертикального 
и бокового 
давлений [2].
Эксперименты показали, что давление является важным параметром, определяющим “память” оттаивающего грунта. Для грунтов массивной и сетчатой криотекстур зависимость относительной осадки оттаивания от давления при оттаивании 
в диапазоне 
близка к прямо пропорциональной (коэффициент корреляции 0,93). При 
прямая пропорциональность S и нарушается, график в этом диапазоне имеет меньший угол наклона, (Рис. 1, кривые 1, 2) [3]. Для грунтов слоистой криотекстуры аппроксимация опытных данных приводит к аналогичному графику, но не проходящему через начало координат (рис. 1, кривая 3).
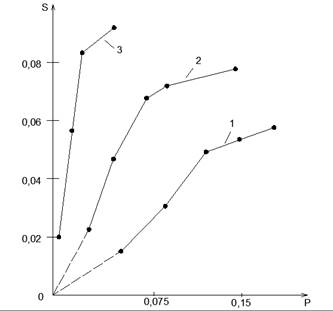
Рис. 1. Зависимость осадки оттаивания от давления:
1 – суглинок массивной криотекстуры 
; 2 – суглинок сетчатой криотекстуры 
; 3 – суглинок слоистой криотекстуры 
Таким образом, зависимость осадки оттаивания от давления может быть представлена в виде кусочно-линейной функции из двух участков и переломом в точке 
, (Рис. 2).
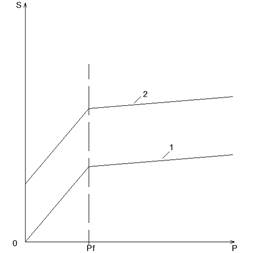
Рис. 2. Схема деформирования грунта при оттаивании:
1 – грунты массивной и сетчатой криотекстуры; 2 – грунты слоистой криотекстуры
В стабилометрических испытаниях возникшие при оттаивании деформации (объемная 
) рассматривались как деформации некоторого условного “упругого тела”, находящегося в аналогичном напряженном состоянии. Для грунтов массивной и сетчатой криотекстур определяемый таким образом “модуль деформации” 
обладает достаточно хорошей воспроизводимостью (табл. 1) и может рассматриваться как инвариантная характеристика деформативности оттаивающего грунта. Анизотропия сжимаемости, характеризуемая величиной 
, равной отношению горизонтальной деформации к вертикальной в условиях всестороннего сжатия (
), для грунтов этих криотекстур невелика [4]. Так, в проведенных опытах различие вертикальной и горизонтальной деформаций при всестороннем сжатии не превышало 13%.
Таблица 1
Деформации суглинка и песка массивной криотекстуры
|
№ опыта |
|
|
|
|
|
|
|
Суглинок, |
||||||
|
1 |
0,05 |
0,05 |
0,037 |
0,098 |
0,87 |
1,18 |
|
2 |
0,075 |
0,0375 |
0,059 |
0,095 |
- |
1,13 |
|
3 |
0,03 |
0,003 |
0,03 |
0,028 |
- |
1,1 |
|
Комп. 1 |
0,075 |
- |
0,063 |
0,063 |
- |
1,17 |
|
Комп. 2 |
0,05 |
- |
0,039 |
0,039 |
- |
1,24 |
|
Песок, |
||||||
|
1 |
0,05 |
0,05 |
0,008 |
0,026 |
0,88 |
3,9 |
|
2 |
0,05 |
0,025 |
0,008 |
0,019 |
- |
3,4 |
|
Комп. 1 |
0,05 |
- |
0,010 |
0,010 |
- |
4,2 |
|
Комп. 2 |
0,025 |
- |
0,008 |
0,008 |
- |
3,3 |
Комп. – компрессионные испытания грунта.
Результаты компрессионных и стабилометрических испытаний обобщаются в следующих соотношениях:
при 
: 
при 
: 
где 
– среднее напряжение при оттаивании и промерзании; 
– коэффициент оттаивающего грунта (условный коэффициент Пуассона), (по проведенным опытам заключен в интервале 0,1 – 0,2); 
– характеристики 2-го линейного участка.
Для грунтов слоистой криотекстуры сочетание напряжений и деформаций не соответствует модели изотропного упругого тела, что приводит к существенному различию формально определяемой величины 
в разных опытах (табл. 2, числитель). В то же время, если разность 
между вертикальной и горизонтальной деформациями оттаивания при всестороннем сжатии рассматривать как дополнительную, не связанную с действующими напряжениями осадку (в приведенном примере 
) и вычесть её из 
во всех опытах, то величина , рассчитываемая по скорректированным таким образом данным, имеет практически тот же разброс, что и для грунтов массивной криотекстуры (табл. 2, знаменатель). Кроме того, величина оказывается довольно близкой к значению ординаты пересечения графика “S - 
” с осью 
в компрессионных испытаниях данного грунта [5].
Таблица 2
Деформации суглинка слоистой криотекстуры, 
|
№ опыта |
|
|
|
|
|
|
|
1 |
0,02 |
0,02 |
|
|
|
|
|
2 |
0,015 |
0,002 |
|
|
- |
|
|
Комп. 1 |
0,03 |
- |
|
|
- |
|
|
Комп. 2 |
0,02 |
- |
|
|
- |
|
Таким образом, общую деформацию при оттаивании грунта слоистой криотекстуры можно представить в виде суммы изотропной компоненты и дополнительной вертикальной составляющей, не зависящей от напряжений, наличие которой обусловливает анизотропию сжимаемости.
Рецензенты:
Олонцев В.Ф., д.т.н., профессор, Пермский национальный исследовательский политехнический университет, г. Пермь;
Овчинников И.Г., д.т.н., доцент, Пермский национальный исследовательский политехнический университет, г. Пермь.