Методический интерес к компьютерной графике вызван потребностью педагогической науки в развитии новой технологии взаимодействия человека и компьютера. Если же визуализировать получаемые данные (например, в виде иллюстраций), то появляется возможность изучать не только алгоритмы и гипотезы, но и графические методы решения задач. Поэтому привлекательным оказывается метод компьютерных иллюстраций с визуализацией учебной информации, особенно математической, который следует рассматривать как современный наглядный метод обучения.
Интерактивная машинная графика представляет собой важный раздел информатики, изучающий динамическое управление пользователем содержанием изображения, его формой, размерами и цветом на дисплее с помощью интерактивных устройств взаимодействия [3].
Иллюстративная функция компьютерной графики обеспечивает наглядность учебного моделирования в методах демонстрационных примеров. Когнитивная функция интерактивной компьютерной графики позволяет с помощью компьютерного изображения получать субъективное новое знание. Для ИКГ-системы важны характер и качество картинок с точки зрения зрительного восприятия, которые влияют на возникновение и продуктивность ИКГ- знаний (гипотез, понятий и представлений) [1, 3].
Убедительным примером развития компьютерных технологий вычислений, машинной графики в науке и образовании является изучение фундаментальных проблем теории чисел, таких как Великая теорема Ферма, нормальное свойство иррациональных чисел, распределение простых чисел в диофантовом пространстве.
Наследием Тьюринга стал компьютер, способный производить за несколько часов вычисления, которые заняли бы у человека непозволительно много времени. Современные компьютеры успевают за долю секунды произвести больше арифметических операций, чем Ферма сделал за всю свою жизнь. Те математики, которые все еще вели неравную борьбу с Великой теоремой Ферма, начали компьютерную атаку на проблему, полагаясь на компьютерную версию подхода, развитого Куммером в XIX в. [4].
Со временем проблемы, связанные с огромным объемом вычислений, стали существенно более доступными. С появлением компьютера большому объему вычислений, связанных с доказательством Великой теоремы Ферма, стало возможно противопоставить быстродействие вычислительных машин. Хорошим примером эффективности компьютерных расчетов в математике может служить история так называемой гипотезы Эйлера (рис. 1).
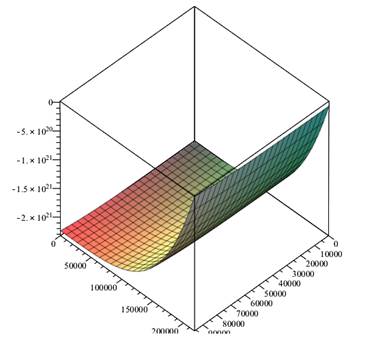
Рис.1. Компьютерная иллюстрация математической гипотезы в интерактивной графике
Эйлер предположил, что уравнение, аналогичное уравнению Ферма, не имеет ненулевых решений в целых числах. На протяжении двух столетий никому не удавалось доказать гипотезу Эйлера, как, впрочем, и опровергнуть ее контрпримером. Ни первые вычисления вручную, ни долгие годы просеивания чисел с помощью компьютеров не позволили обнаружить ни одного решения. Отсутствие контрпримера воспринималось как убедительное свидетельство в пользу гипотезы Эйлера. Но в 1988 г. Наум Элькис из Гарвардского университета нашел решение. А Роджер Фрай, затратив 110 ч работы суперкомпьютера Connection Machine, обнаружил другое решение уравнения Эйлера [4].
Обманчивый характер гипотезы о завышенной оценке количества простых чисел также является фундаментальной проблемой теории чисел. В 1791 г. Карл Гаусс, которому было тогда всего лишь 14 лет, сформулировал приближенный закон, по которому уменьшается частота простых чисел. Формула Гаусса давала разумную точность, но всегда слегка завышала истинное распределение простых чисел. В 1914 г. Дж. И. Литлвуд, сотрудник Г.Г. Харди по Кембриджскому университету, доказал, что для очень больших чисел формула Гаусса даст заниженную оценку распределения простых чисел. В 1955 г. С. Скьюз показал, что недооценка количества простых чисел может наступить прежде, чем будет достигнуто некоторое число. Это число невозможно даже представить, и никаких практических приложений оно не имеет. Харди назвал число Скьюза «самым большим числом, которое когда-либо служило какой-нибудь цели в математике» [4].
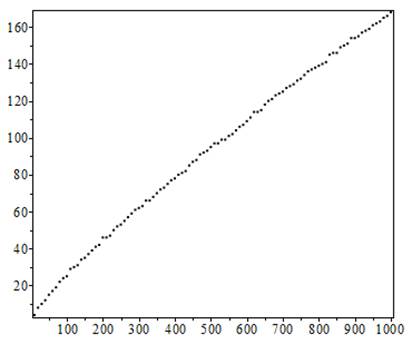
Рис. 2. Распределение простых чисел в компьютерной среде Maple
Исторически особое место в исследовании гипотез занимала геометрия, а впоследствии компьютерный графический метод. В ХХ в. геометры достигли глубокого и тонкого понимания математических объектов, в частности свойств поверхностей. В 1970-е гг. российский математик С. Аракелов попытался установить параллели между проблемами алгебраической геометрии и проблемами теории чисел. Это было одно из направлений программы Ленглендса, и математики надеялись, что нерешенные проблемы теории чисел удастся решить, изучая соответствующие проблемы геометрии, которые также еще оставались нерешенными. Такая программа была известна под названием философии параллелизма. Те алгебраические геометры, которые пытались решать проблемы теории чисел, получили название арифметических алгебраических геометров.
В 1983 г. геометры возвестили о своей первой значительной победе, когда Герд Фалтингс из Принстонского Института высших исследований внес существенный вклад в понимание теоремы Ферма. Фалтингс решил, что ему удалось продвинуться в доказательстве Великой теоремы Ферма с помощью изучения геометрических поверхностей, связанных с различными значениями n. Поверхности, связанные с уравнениями Ферма при различных значениях n , отличаются друг от друга, но обладают одним общим свойством — у них всех имеются сквозные отверстия, или, попросту говоря, дыры. Фалтингсу удалось доказать, что, поскольку такие поверхности всегда имеют несколько дыр, связанное с ними уравнение Ферма могло бы иметь лишь конечное множество решений в целых числах. Таким образом, Фалтингс не доказал Великую теорему Ферма, но по крайней мере сумел отвергнуть возможность существования у уравнения Ферма бесконечно многих решений [4].
Введение иррациональных чисел означало гигантский прорыв в математике. Математики получили возможность бросить взгляд за пределы целых чисел и обыкновенных дробей, оглядеться и открывать или, быть может, изобретать новые числа. По словам математика XIX в. Леопольда Кронекера: «Бог создал целые числа; все остальное дело рук человеческих».
Самым замечательным иррациональным числом по праву считается число π. В действительности число π невозможно точно представить в виде десятичной дроби, так как десятичная дробь получается бесконечной и в распределении цифр нет никакой закономерности. Свойство иррациональности числа π, т. е. непредставимость его в виде отношения двух целых чисел, доказали Иоганн Ламберт (1728–1777) и Адриен Лежандр (1752-–1833) в конце XVIII в. Свойство трансцендентности означает, что число π не является корнем никакого многочлена с целыми коэффициентами. Это свойство было доказано немецким математиком Фердинандом Линдеманом (1852–1939) в 1882 г. В настоящее время ведутся исследования по уточнению «тонкой структуры» числа π [2].
Экспериментируя с алгоритмами на компьютере, возможно знакомство с нормальным свойством мантиссы числа, которое определил французский математик Эмиль Борель в 1909 г. Положительное число, меньшее единицы, называется нормальным, если в его десятичной записи любая комбинация цифр встречается одинаково часто. Это определение можно распространить и на другие, недесятичные системы счисления. В настоящее время в математике неизвестно, является ли дробная часть числа π слабо нормальной к основанию 10 или к какому-либо другому основанию в общем случае [2].
Тем не менее результаты учебных компьютерных экспериментов, например в системе символьной математики Maple, подтверждают слабо нормальное свойство числа π для частных случаев. На рисунке 3 представлены сюжет «Черно-белое поле числа π», наглядная графическая иллюстрация одномерных и двумерных кортежей в структуре фундаментальной константы на компьютере. Цифры двоичной кодировки представлены белым и черным цветом. Примечательно, что при заданной выборке массива данных число белых квадратиков примерно совпадает с числом черных. Данная иллюстрация — это также одно из проявлений гипотетического нормального свойства числа π [5].

Рис. 3. Иллюстрация гипотезы о нормальном свойстве числа π
Статистические результаты исследования нормального свойства числа π с использованием современного программного обеспечения представлены в статье [5]. При увеличении размерности массива данных ширина распределения погрешности вычислений уменьшается и смещается к нулю, что также иллюстрирует гипотетическое свойство иррационального числа (рис. 4).
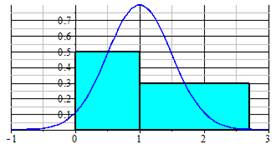
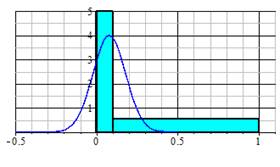
Рис. 4. Иллюстрация гипотезы о нормальном свойстве иррационального числа
Заключение
Осталось превеликое множество нерешенных научных проблем, которые представляют интерес в методике учебных исследований. Многие из них, как и Великая теорема Ферма, уходят корнями в древнегреческую математику c понятными формулировками. Но множество загадок и поныне связано с простыми и совершенными числами. В частности, пока не доказана четность совершенных чисел [4]. Другая сложная проблема, связанная с совершенными числами, состоит в выяснении ответа на вопрос, можно ли исчерпать запас совершенных чисел за конечное число шагов. На протяжении веков многие математики, занимающиеся теорией чисел, пытались выяснить, конечно или бесконечно множество совершенных чисел, но всякий раз терпели неудачу. Всякому, кому удалось бы дать определенный ответ на этот вопрос, уготовано почетное место в истории математики.
2000 лет назад Евклид доказал, что запас простых чисел неисчерпаем. Последние два столетия математики пытались доказать, что запас простых чисел-близнецов также неисчерпаем. Существуют веские основания полагать, что множество простых чисел-близнецов бесконечно, но никому пока не удалось доказать, что это действительно так.
Еще одна загадка простых чисел восходит к работам Христиана Гольдбаха 1742 г., в частности утверждение, что каждое четное число представимо в виде суммы двух простых чисел. Ныне, в век компьютеров, гипотезу Гольдбаха подвергли проверке. Оказалось, что она верна для любого четного числа до 100 000 000, но доказать, что она верна для любого из бесконечно многих четных чисел, пока никому не удалось [4].
За последние сотни лет никому не удалось доказать, что гранецентрированная кубическая решетка действительно служит оптимальной стратегией упаковки шаров. Но никто пока не открыл более эффективного метода упаковки. Отсутствие контрпримера означает, что для всех практических целей утверждение Кеплера применимо, но в абсолютном мире математики абсолютно необходимо строгое доказательство. Гипотеза Кеплера утверждает, что среди бесконечно многих вариантов расположения шаров нет ни одного такого, у которого коэффициент заполнения пространства был бы больше, чем у гранецентрированной кубической решетки. Математикам предстоит доказать, что это невозможно не только для регулярного, но и для случайного, хаотического, варианта расположения шаров. Британский специалист по упаковке шаров К.А. Роджерс говорит, что «большинство математиков в правильность гипотезы Кеплера верят, а все физики в ее правильности твердо убеждены, так как это знают».
Наиболее высокий, результативный уровень творческой деятельности в образовании характеризуется умением формулировать гипотезу, сравнивать между собой различные данные, абстрагироваться и выделять существенное, проводить аналогии, стимулировать творческую фантазию. В этом отношении возможности математических дисциплин, компьютерного эксперимента и интерактивной графики в учебных исследованиях представляют предмет современных научных исследований в методической науке.
Рецензенты:
Щитов И.Н., д.ф.-м.н., профессор, профессор Санкт-Петербургского государственного института кино и телевидения Министерства культуры РФ, г. Санкт-Петербург;
Смирнов Н.В., д.ф.-м.н., доцент, профессор кафедры моделирования экономических систем факультета прикладной математики — процессов управления Санкт-Петербургского государственного университета Министерства образования и науки РФ, г. Санкт-Петербург.



