Ситуация в экономике и в обществе в целом, сложившаяся за последние полтора года в связи с экономическими санкциями Запада, продемонстрировала ошибочность курса на производство системой образования «квалифицированных пользователей» импортных разработок, технологий и оборудования − вместо воспитания собственных инженеров, способных создавать новые технологии и оборудование самостоятельно. В связи с этим роль естественно-научного и инженерного образования в ближайшие годы должна расти. Однако за последние два десятилетия сформировалась устойчивая ориентация выпускников школ на получение экономического, юридического и иного гуманитарного образования. Молодые люди по большей части желают управлять − финансами, предприятиями, политической и социальной сферами, при этом совершенно не достаточно тех, кто хочет и может разрабатывать и производить высокотехнологичную продукцию как в виде товаров, так и в виде услуг (к которым сегодня относят медицину и образование).
Разумеется, эта ситуация в системе образовании может измениться только в результате продуманных и согласованных действий государства и общества, причем не в виде краткой кампании, а в виде долговременной «новой образовательной политики», радикально отличающейся от проводившейся последние полтора десятка лет.
Одним из путей возрождения интереса учащихся к естественно-научному образованию, научно-техническому творчеству и инженерному делу является внедрение в систему среднего образования механизмов формирования у школьников эмпирического мышления и умения проводить учебный эксперимент. При этом следует использовать как классические, так и новые инструменты развития этого интереса. Примером удачного новшества является введение в учебный план многих школ курса робототехники. Что касается компьютерных технологий, то использование их потенциала остается недостаточно эффективным.
Среди методистов по-прежнему остается распространенной точка зрения, что компьютерная модель не является полноценной заменой реальных объектов и явлений и потому не может быть полезной для развития эмпирического мышления учащихся. Насколько правдоподобна первая часть этого утверждения (к обсуждению которой вернемся позднее), настолько сомнительна вторая. Полагаем, что говорить о формировании элементов эмпирического мышления и умений, необходимых для проведения эксперимента, на основе интерактивных компьютерных моделей и тренажеров вполне можно, хотя, разумеется, ведущая роль в этом процессе принадлежит реальному лабораторному эксперименту.
Традиционно в эмпирическом исследовании выделяют [3] следующие стадии, связанные, в том числе, и с эмпирическим мышлением:
1) наблюдение и эксперимент – средство получения данных опыта;
2) анализ и синтез результатов – средство выявления связей и систематизации данных;
3) обобщение данных опыта, формирование новых эмпирических понятий и законов (с последующей проверкой), позволяющих в дальнейшем дать объяснение изучаемому феномену и прогнозировать поведение системы.
Вторая и третья стадии осуществляются в модельном эксперименте полноценно, за исключением того, что анализируется и обобщается: остается проблема самой процедуры получения экспериментальных данных − если речь идет о компьютерной имитации реальной экспериментальной установки. Больше всего страдает при таком имитационном эксперименте первая стадия исследования: обедняется чувственная сторона процесса познания, разрывается связь с объективной реальностью. Эти потери невосполнимы на этапах проектирования (сборки) экспериментальной установки и собственно выполнения наблюдений и измерений. Однако первая стадия включает в себя также этапы формулирования проблемы исследования, выдвижения и обоснования гипотезы, на основе которой проблему можно решить, определения цели эксперимента и порядка его проведения. Если же компьютерная система не просто имитирует реальную установку, а на достаточно высоком уровне абстракции моделирует некоторое сложное явление (например, установление хаоса в системе многих частиц), то и этап получения данных путем измерений на компьютерной модели становится полноценным, а учебное исследование приближается к научному.
Интерактивным моделям учебного назначения, как и научно-исследовательским, присущи определенные гносеологические функции [1−2], определяющие их дидактические и методологические функции. Дидактические функции учебных моделей связывают [4] с возможностями их использования как средства наглядности при предъявлении знания, как средства отработки познавательных умений и формирования навыков, а также как средства контроля уровня сформированности знаний и умений учащихся. Основная методологическая функция моделей, сформулированная в той же работе, – формирование у школьников опыта учебного исследования, в ходе которого происходит получение субъективно нового знания, а модельный эксперимент выступает в качестве метода познания.
Преломление процесса научного познания в образовательном процессе обсуждается и в учебном издании [5]. Как и реальный эксперимент, компьютерное моделирование поддерживает важные этапы учебного исследования. Оно может быть использовано, чтобы:
- проводить наблюдение, классификацию и обобщение фактов, в том числе замечать сходство и закономерности результатов;
- проводить интерпретацию данных;
- давать объяснение наблюдаемым явлениям и выдвигать гипотезы;
- планировать модельный эксперимент для проверки гипотезы и проводить его;
- делать выводы и заключения на основе проведенных исследований.
Одним из важных признаков сформированности эмпирического мышления является умение продумывать тактику проведения эксперимента, которая бы полно, но экономно в плане потребных усилий позволяла решить проблему исследования. И в этом смысле работа с физической установкой и с адекватной ей в рамках поставленной задачи компьютерной моделью схожа и практически в одинаковой степени полезна. В обоих случаях наиболее важными являются: а) мыслительные процессы, происходящие в мозгу учащегося; б) технические возможности «лабораторного стенда» по проверке и, при необходимости, коррекции гипотезы исследования, исправление ошибок за счет оперативной обратной связи, которую обеспечивают измерительные приборы или интерфейс модели. При этом реальный лабораторный стенд, конечно же, много богаче по своим свойствам и их проявлениям, чем имитирующий его стенд виртуальный, но для изучения ряда вопросов, в том числе тактики проведения исследования, это может быть несущественным.
Наиболее показательными для иллюстрации сказанного представляются модельные эксперименты, позволяющие получить на выходе не качественную зависимость, пусть даже иллюстрируемую графиком, а количественную, выраженную формулой или набором специфических для данной ситуации числовых значений.
Примером ситуации, рассмотрение которой полезно для освоения умения планировать эксперимент, может служить классическая задача о бросании тела под углом к горизонту над наклонной плоскостью – «бросания в гору». Эта задача входит в качестве самостоятельного элемента, например, в состав моделирующей среды «Интер@ктивная физика» (Институт инновационных технологий, г. Пермь), но может быть рассмотрена и на моделях ряда других электронных изданий учебного назначения.
Пусть модель позволяет устанавливать перед броском (или выстрелом) угол j наклона «подстилающей поверхности» и угол a между вектором начальной скорости тела и горизонталью, а также фиксировать перемещение L тела вдоль плоскости в момент падения на нее (рис. 1). В этом случае целью проведения модельного эксперимента можно поставить отыскание зависимости amax(j) – величины угла бросания, при котором дальность полета максимальна, от значения угла наклона плоскости.

Рис. 1. Модельный эксперимент: зависимость дальности полета тела от угла бросания и угла наклона подстилающей поверхности.
Самостоятельное планирование учащимся соответствующего исследования на основе компьютерной модели требует определенных навыков и опыта такого рода работы. Не обладающий навыками проведения эксперимента (неважно, физического или численного) школьник часто даже не понимает, что начальные условия нельзя менять хаотически, нужно продумать систему – например, в нашем случае не следует менять скорость бросания. Специфика работы с компьютерными моделями обычно уясняется либо благодаря инструкциям по их исследованию (типа порядка выполнения лабораторных работ), либо в ходе проблемных бесед, которые проводит с классом учитель [1]. Для обсуждаемой задачи основой плана работы и своеобразной посказкой может служить порядок модельного эксперимента при бросании тела над горизонтальной поверхностью (j=0). Его идея в том, чтобы начать эксперимент с небольшого значения угла a, а затем продолжать броски, каждый раз увеличивая угол бросания на одинаковую величину, например, на 5º. При этом обнаруживается, что максимальная дальность полета достигается при угле бросания 45º, а пары значений угла, дающие в сумме 90º, приводят к одинаковой дальности полета.
Учащемуся остается сообразить, что в случае наклонной «подстилающей поверхности» нужно провести серию аналогичных экспериментов с разными значениями угла j, определив для каждого из них соответствующий amax. Для дальнейшего анализа результатов пары значений j и amax следует занести в таблицу; желательно построить иллюстрирующий обнаруженную зависимость график. Далее нужно заметить, что зависимость имеет линейный характер, и записать ее в виде искомой функции: amax=45º+j/2.
Заметим, что навык математической записи такого рода зависимостей по данным таблицы или по графику может отрабатываться при помощи интерактивного компьютерного тренажера. То же касается умения проектировать структуру таблиц данных, являющегося элементом культуры проведения эксперимента. Поскольку с точки зрения физики это в основном технический вопрос, операциональный навык, он может отрабатываться в рамках компьютерного тренажера не только на базе физического эксперимента, но и на базе имитационной модели и даже – для экономии времени – видеозаписи эксперимента или анимации. Еще ряд тренажеров может быть полезен для освоения процедур снятия показаний измерительных приборов и оценки связанных с ними погрешностей, записи результата эксперимента в виде доверительного интервала с разумной точностью, а не с 8–10 значащими цифрами, которые дает калькулятор. Экспертная система интерактивного тренажера отслеживает в ходе работы ошибки учащегося, контекстно реагирует на них.
По нашим наблюдениям, использование компьютера эффективно именно при отработке элементарных навыков. Однако, разумеется, необходимы этапы обучения, на которых все умения и навыки включены в «сплошной» процесс проведения эксперимента, и здесь эксперимент должен быть уже не виртуальным, а реальным. Таким образом, компьютерные тренажеры снимают с учителя рутинную работу – многократное объяснение и контроль базовых умений и навыков – и позволяют ему сосредоточиться на более сложных, творческих, трудно алгоритмизируемых моментах. Использовать такие тренажеры в принципе или нет – решение конкретного преподавателя; дело разработчика программно-методического обеспечения предложить саму возможность их использования.
Затронем теперь два момента, связанных с проблемой достоверности результатов математического моделирования: 1) адекватность модели изучаемого объекта и 2) адекватность численного метода решения ее системы уравнений.
Назначение всякой модели – прежде всего, помочь исследователю понять то или иное явление природы. С другой стороны, предполагается, что результаты моделирования и их логические следствия дают возможность предсказывать поведение объекта в заданных (но, как правило, ограниченных в своем разнообразии некоторыми рамками) условиях. Если хотя бы некоторые варианты этих условий реализуемы в лабораторном или натурном эксперименте, необходимо проведение сравнения (прямого или косвенного) экспериментальных данных и результатов расчета; иначе говоря – необходимо тестирование модели. Соответствие экспериментальной и расчетной информации говорит в пользу построенной модели. Напротив, значительные расхождения, которые нельзя приписать погрешностям опыта, или невозможность интерпретировать результаты моделирования с точки зрения данных эксперимента, означают, что модель не является адекватной, пригодной для описания объективного мира и должна быть усовершенствована. Чем больше изучено ситуаций, в которых модель оказалась способна корректно воспроизвести реальность, тем с большим основанием можно использовать ее при описании соответствующих эффектов в сходных условиях. Однако всякая, условно говоря, «интерполяция», а тем более «экстраполяция» в неисследованную область условий сопряжена с определенным риском. То же касается моделей, реальный прообраз которых по каким-либо причинам не пригоден или не доступен для манипуляций. В любом случае каждая модель имеет определенную область применимости, говорить об адекватности можно лишь в пределах этой области, и дело исследователя – следить за тем, чтобы не перейти ее границы.
Теперь об адекватности численного метода. В вычислительной математике разработано значительное число методов численного решения задачи интегрирования систем дифференциальных уравнений при заданных начальных условиях (задачи Коши). Эти методы обладают различными характеристиками, прежде всего – точностью и объемом производимых вычислений. Ошибка или погрешность расчета при использовании конкретного численного метода складывается из методической ошибки (неточность самого алгоритма, вызванная, например, отсечением членов бесконечного ряда) и ошибки округления, вызываемой ограниченным количеством разрядов (конечной длиной машинного слова). Поэтому характер накопления и распространения ошибки с увеличением числа шагов существенно зависит от выбранного метода, реализующего этот метод алгоритма.
Возращаясь к вопросу о корректности замены реальных объектов и явлений компьютерной моделью, отметим, что модель не обязана описывать все стороны явления и варианты протекания связанных с ними событий. То есть эти качества сами по себе хороши, особенно если речь идет о модельном конструкторе, на базе которого предполагается решать широкий класс задач, а основанный на этом конструкторе конкретный лабораторный стенд не получается «неподъемным» с точки зрения скорости вычислений и сложности интерфейса. Однако если речь идет об отдельной лабораторной работе, достаточно, чтобы модель лишь соответствовала цели эксперимента. В рассмотренном выше примере также нет нужды в сложной модели. Например, модель изображенная на рисунке 1, описывает многократные отскоки мячика от наклонной плоскости в вязкой среде, поскольку построена на базе весьма универсального конструктора, элементы которого содержат уравнения движения и процедуру их интегрирования для пространственной области с изменяемыми свойствами среды внутри нее и на ее границах. Однако эти возможности в рамках лабораторной работы не используются, так что совершенно достаточной была бы модель, построеннная на простейших кинематических уравнениях или даже уравнении параболы, коэффициенты в котором вычисляются по начальным условиям движения.
Другим примером компьютерной модели, позволяющей получить в результате ее исследования формулу, является мост Уитстона. Целью исследования может быть выяснение условий баланса плеч моста (отсутствия тока в гальванометре). На рисунке 2 представлен интерфейс такой модели: в начальном состоянии все сопротивления одинаковы, но могут изменяться пользователем в ходе эксперимента. Сначала учащиеся обнаруживают, что баланс сохраняется, если изменить в одинаковое число раз сопротивления двух смежных плеч моста. К обобщению этого результата, пониманию того, что различными могут быть значения всех четырех сопротивлений, школьника с несформированными в достаточной степени исследовательскими навыками, может быть, необходимо подтолкнуть (с помощью текста инструкции, в ходе диалога с учителем или экспертной системой). Результатом исследования является известная пропорция вида: R1/R3 = R2/R4. Достоинством компьютерной модели в этом случае является возможность за короткое время рассмотреть большое число ситуаций, на базе которых можно проанализировать результаты и сделать вывод. После изучения физической системы в ее модельном варианте учащиеся лучше воспринимают теоретическое объяснение найденной закономерности.
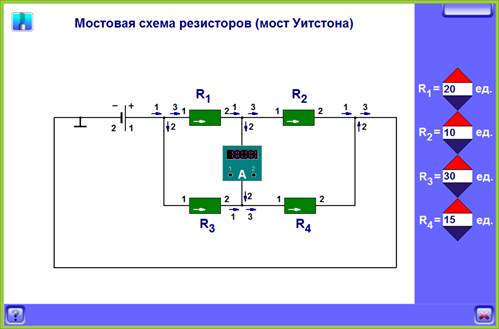
Рис. 2. Модельный эксперимент: выяснение условия баланса моста Уитстона
Заменяют ли тренажеры-имитаторы транспортных средств или промышленных установок соответствующую реальность? Разумеется, не заменяют. Однако позволяют подготовиться к восприятию этой реальности, «помыслить» себя в сходной ситуации. Аналогично, реальный эксперимент нельзя заменять в учебном процессе компьютерными технологиями, но при наличии продуманной методики последние могут служить дополнительным инструментом, средством обучающего воздействия, которое позволяет экономить время и усилия учителя, отрабатывать умения и навыки, в том числе связанные с экспериментальной деятельностью, и даже формировать эмпирическое мышление.
Рецензенты:
Оспенникова Е.В., д.п.н., профессор, зав. каф. мультимедийной дидактики и информационных технологий обучения Пермского государственного гуманитарно-педагогического университета, г. Пермь;
Серова Т.С., д.п.н., профессор кафедры иностранных языков, лингвистики и перевода Пермского национального исследовательского политехнического университета, г. Пермь.



