Как известно, в прикладных технических науках существуют численные и аналитические способы расчета, при этом каждый из них, имеет свои достоинства и недостатки. По этой причине в сложных расчетах применяются оба этих способа, в той мере, в какой каждый из них позволяет добиться желаемой точности при наименьших временных и аппаратных затратах.
В настоящее время широкое развитие средств ПК вывели на первое место численные методы расчета, однако аналитический подход остается востребованным благодаря красоте и наглядности представления результатов, возможности воспроизвести решение в любой точке расчетного пространства, а также произвести различного рода математические операции (интегрирование, дифференцирование, и т. д.), получив в результате непрерывные, гладкие функции.
На сегодняшний день имеется большой выбор математических методов и приемов, позволяющих аппроксимировать непрерывные и гладкие кривые, а также научных работ, посвященных этой тематике [1 – 3]. В данной статье предложен метод экспоненциальных кривых с полиномиальными показателями, позволяющий расширить инструментарий инженеров-проектировщиков и научных работников в построении моделей технических процессов и устройств.
Постановка задачи
Как известно, многие вольт-амперные характеристики (полупроводникового диода, биполярного и полевых транзисторов) имеют вид экспоненты [4,5]. Однако при описании вышеперечисленных характеристик этим классом кривых, возникают определенные трудности и значительные расхождения с экспериментом на их отдельных участках.
Так, например, широко известное в электронике уравнение Шокли
(где 
– ток насыщения, 
– температурный потенциал), не может описать с достаточной для инженерных расчетов точностью (хотя бы на участке напряжений 
) вольтамперную характеристику диода в силу ряда процессов, происходящих в объеме p-n перехода под действием внешнего напряжения [4, 5]. Значит, для описания подобных процессов нужно ввести некую модифицированную экспоненту, параметры которой позволили бы приблизить ее к экспериментальным кривым с необходимой точностью.
Такая кривая может быть описана функцией вида
или, в более удобном для расчетов виде
где 
Следует отметить, что такое представление не лишено физического смысла, поскольку полином 
может (по крайней мере, теоретически) представлять собой разложение в ряд Маклорена некоей сложной функции. При этом (как показано ниже), добавление членов ряда позволяет увеличить точность аппроксимации (при условии, что экспериментальная кривая принадлежит к классу экспонент).
Очевидно, что функции (1.2) и (1.3) являются гладкими непрерывными и бесконечно дифференцируемыми, что позволяет осуществлять с ними все перечисленные выше математические операции.
Описание метода
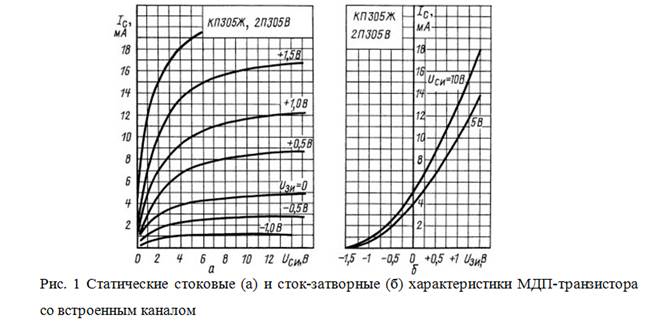
Как известно, состояние полевых транзисторов в стационарном температурном режиме описывается стоковыми и сток-затворными характеристиками. На рис. 1 приведены такие характеристики для одного из типов транзисторов.
Видно, что сток-затворная характеристика имеет ярко выраженный экспоненциальный вид. Однако применение для её аппроксимации кривой вида (1.1) не оправдано, поскольку ведет к значительным расхождением с экспериментом (см. рис. 2).
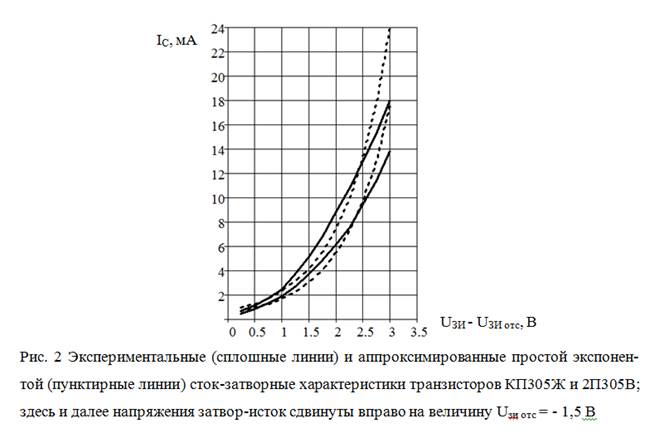
Экспоненциальные зависимости для сток-затворных характеристик (рис. 2) были получены широко известными в прикладной математике уравнениями регрессии [6], коэффициенты которых определяют отысканием экстремума некоего функционала
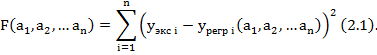
Вычислив частные производные, получим следующую систему уравнений для отыскания неизвестных коэффициентов 
:
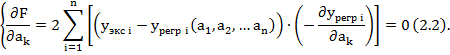
В случае с экспоненциальной кривой 
, удобнее работать не с самим вектором 
, а с его логарифмом, что значительно упрощает вычисления, поскольку
что приводит к линейному уравнению регрессии.
Применим для аппроксимации экспоненту с показателем в виде квадратичного полинома:
где 
– аппроксимированные значения тока стока.
Тогда, согласно (2.3), получим:
При этом система уравнений (2.2) примет вид:
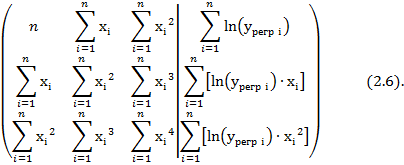
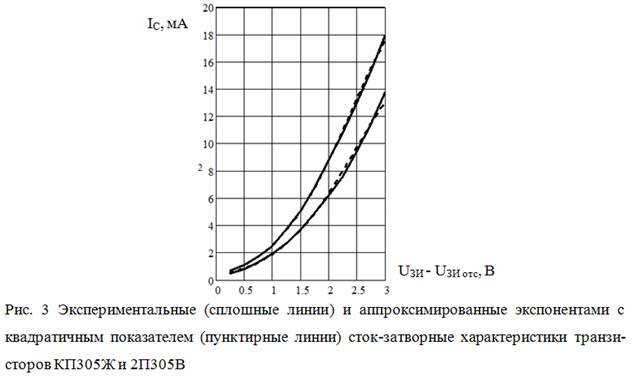
Полученные таким образом кривые представлены на рис. 3, в сравнении с экспериментальными зависимостями, показывая лучшую точность их воспроизведения.
Однако при высоких напряжениях UЗИ наблюдается некоторое расхождение в производной аппроксимированной функции с экспериментальной, что может привести к неточностям при вычислении крутизны характеристики S = dIС/dUЗИ. Повысим степень полинома до 3-х, при этом получим следующую систему уравнений:
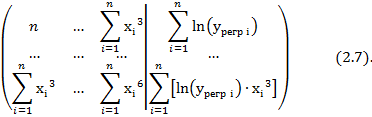
Результаты такой аппроксимации представлены на рис. 4; они показывают, что с ростом степени полинома кривые аппроксимации сходятся к форме экспериментальных кривых.
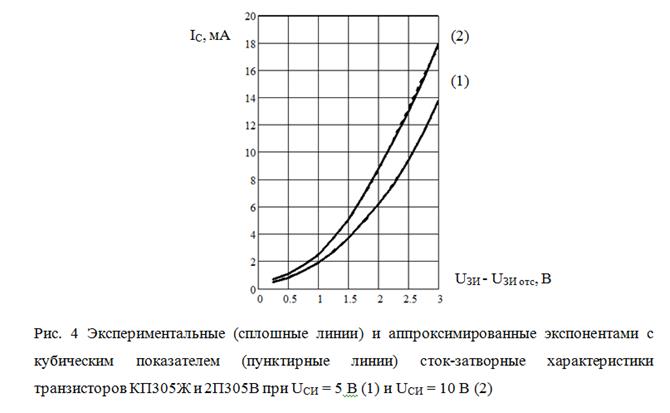
Близкая к эксперименту форма кривых показывает нецелесообразность дальнейшего повышения степени полинома в показателе экспоненты, поэтому окончательно искомые кривые выражаются следующими аналитическими формулами:
где 
Для исследованных сток-затворных характеристик ниже приведены рассчитанные коэффициенты 
(в виде вектора 
) и 
(в виде матрицы A).
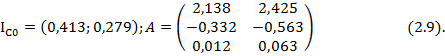
Замечание. Введение новой переменной 
обусловлено тем, что функция логарифма не существует при отрицательных аргументах. Более того, как показали расчеты, приближение величины к нулю ведет к значительным расхождениям кривых аппроксимации с экспериментальными характеристиками, что можно считать техническим недостатком данного метода.
Проделаем аналогичные вычисления для стоковых характеристик (рис. 1). Как показывают расчеты, хорошая точность аппроксимации для них также получается при кубической степени полинома в показателе экспоненты. Но теперь в виде функции должна быть взята величина напряжения сток-исток UСИ, а ток стока – аргументом. Несомненно, такое представление создает определенные неудобства, поскольку вольтамперные характеристики это зависимости типа I(U), но это неудобство имеет технический, а не принципиальный характер, поскольку, с точки зрения математического анализа, представления функции в виде y(x) и x(y) равноправны.
Таким образом, кривые аппроксимации для стоковых характеристик имеют следующий вид:
где 
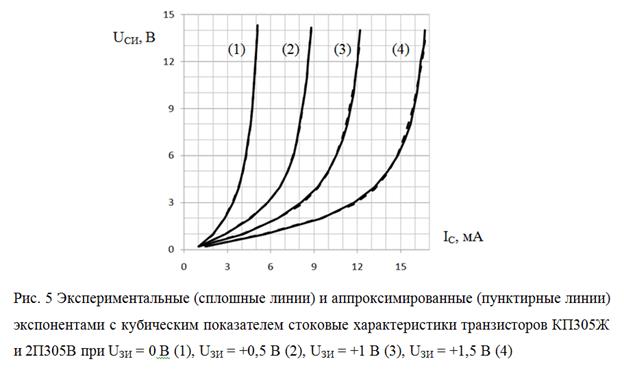
Результаты такой аппроксимации приведены на рис. 5, который показывает их хорошее совпадение с экспериментальными кривыми, приведенными на рис. 1.
Для исследованных стоковых характеристик ниже приведены рассчитанные коэффициенты 
(в виде вектора 
) и 
(в виде матрицы B).
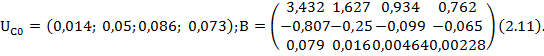
Результаты и выводы
Все изложенное дает основание считать данный метод применимым для практических расчетов в области электроники и схемотехники по следующим причинам:
1. Как было доказано расчетами, стоящий в степени полином дает возможность добиваться нужной точности в отображении экспериментальных кривых путем увеличения его степени.
2. Метод не является трудоемким, поскольку базируется на широко известном методе наименьших квадратов и общих принципах отыскания уравнений регрессии.
3. Представленные кривые являются непрерывными и гладкими, что позволяет использовать не только сами кривые, но и их производные.
В самом деле, для производной dIC/d(∆UЗИ) получим:
которая, как известно, является крутизной характеристики S.
Производная dUСИk/dIC также рассчитывается в соответствии с правилами математического анализа. Из (2.10) получим:
Как известно из электроники, данная производная является выходным сопротивлением полевого транзистора для переменного сигнала.
Недостатки метода уже упоминались выше. Это трудность описания кривых в области нуля по той переменной, к которой должна быть применена операция логарифмирования, а также некоторая громоздкость аналитической формулы, по сравнению с формулами и зависимостями, описывающими подобные характеристики на кусочных интервалах.
Рецензенты:
Лаврентьев А.А., д.ф.-м.н., профессор, заведующий кафедрой электротехники и электроники ДГТУ, г. Ростов-на-Дону;
Звездина М.Ю., д.ф.-м.н., доцент, заведующая кафедрой радиоэлектроники ДГТУ, г. Ростов-на-Дону.