Неотъемлемой частью обучения в старших классах школы становится профильная дифференциация. В рамках профильной дифференциации необходимо проводить факультативы и спецкурсы по прикладной математике, программированию, применению численных методов в решении математических задач. Поэтому задачей учителя становится интеграция математики и информатики через взаимопроникновение тем, методов, ресурсов, компьютерных математических программ. В результате необходимо обучать студентов созданию интегрированных курсов по математике и информатике.
Таким образом, одной из приоритетных задач методики обучения информатике является обучение студентов реализации данных межпредметных связей, а конкретно – разработка интегрированных факультативных и элективных курсов [2, 3].
Для реализации такого обучения нами разработан спецкурс «Реализация профильной дифференциации обучения информатике», целью которого является разработка профильных межпредметных элективных курсов студентами – будущими учителями информатики.
В качестве примера вышеназванного курса со студентами может быть рассмотрен межпредметный элективный курс «Решение задач с параметрами».
В качестве математической основы элективного курса было выбрано решение задач с параметрами. Подобные задачи присутствуют практически в любом вступительном испытании. Часть С ЕГЭ по математике также содержит задачу с параметром.
Сама задача с параметром может быть рассмотрена как аналог научно-исследовательских задач прикладной математики. А.Г. Мордкович оценивал задачи с параметром как «один из труднейших разделов школьного курса математики, в котором, кроме использования определенных алгоритмов решения уравнений и неравенств, приходится обдумывать, по какому признаку нужно разбить множество значений параметра на классы, следить за тем, чтобы не пропустить какие-либо тонкости» [1, с. 3].
Таким образом, обучение решению задач с параметрами, с одной стороны, способствует развитию исследовательских умений учащихся, повышению логической культуры, общих математических знаний, развитию творческого потенциала ученика и мотивации к обучению математике, а с другой – является необходимой подготовкой к итоговому испытанию. В качестве компьютерной составляющей мы остановили выбор на программе GeoGebra. Также несколько заданий для примера решаются в математическом пакете MathCAD.
GeoGebra – бесплатная программа, предоставляющая возможность создания динамических («живых») чертежей для использования на разных уровнях обучения геометрии, алгебры, планиметрии и других смежных дисциплин. Программа обладает богатыми возможностями работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.). В отличие от других программ для динамического манипулирования геометрическими объектами, идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления.
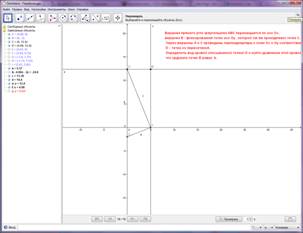
Рис. 1. Вид программный среды GeoGebra
Структура программы состоит из двух образовательных блоков: теория и практика.
Программа курса рассчитана на 17 часов. Периодичность занятий 1 раз в неделю.
Логика освоения углубленных тем определяется следующими задачами:
- изучение дополнительного материала;
- овладение системой математических знаний и умений;
- приобретение исследовательских компетенций – поиск функциональных связей и отношений между частями целого; разделение процессов на этапы, звенья;
- воспитание культуры личности, понимание значимости математики в научно-техническом прогрессе;
- развитие качеств личности, необходимых человеку в современном обществе.
Все образовательные блоки предусматривают не только усвоение теоретических знаний, но и накопление деятельностно-практического опыта.
Разработанный курс позволяет формировать умения по решению задач с параметрами, сводящихся к исследованию линейных и квадратных уравнений и неравенств.
Результаты по данному курсу достигаются в каждом образовательном блоке. В планирование содержания включены контрольные уроки.
В результате работы по программе « Решение уравнений и неравенств с параметрами с компьютерной поддержкой» девятиклассники должны:
1) знать определение параметра, «что значит решить задачу с параметром», основные типы решения уравнений и неравенств с параметрами, основные способы решения уравнений и неравенств с параметрами;
2) уметь исследовать и решать задачи с параметрами на основе алгоритма решения, применять тот или иной способ при решении заданий с параметрами.
Таблица 1
Тематическое планирование курса
|
№ |
Тема |
Количество часов |
Форма проведения |
|
1 |
Знакомство с параметрами |
1 |
Лекция |
|
2 |
Решение линейных уравнений, содержащих параметры |
1 |
Практическое занятие |
|
3 |
Решение линейных неравенств, содержащих параметры |
1 |
Практическое занятие |
|
4 |
Решение квадратных уравнений, содержащих параметры |
1 |
Практическое занятие |
|
5 |
Решение квадратных неравенств, содержащих параметры |
1 |
Практическое занятие |
|
6 |
Решение тригонометрических уравнений, содержащих параметры |
2 |
Практическое занятие |
|
7 |
Решение тригонометрических неравенств, содержащих параметры |
2 |
Практическое занятие |
|
8 |
Текстовые задачи с параметрами |
1 |
Практическое занятие |
|
9 |
Производная и ее применения |
2 |
Практическое занятие |
|
10 |
Нестандартные задачи с параметрами |
3 |
Практическое занятие |
|
11 |
Представление докладов |
2 |
Семинарское занятие |
|
|
Итого: |
17 |
|
Рассмотрим более подробно содержание Темы 2 «Решение линейных уравнений, содержащих параметры».
Предлагается на рассмотрение следующая задача: 
В этой задаче 
обозначено за неизвестное число, а буква 
выполняет роль известного фиксированного числа. Это уравнение является линейным уравнением с параметром . Предлагается определить, при каких значениях уравнение будет иметь один корень.
Придавая в различные значения, мы будем получать различные уравнения с числовыми коэффициентами.
Перед аналитическим решением задачи мы можем продемонстрировать ученикам наглядную трактовку ее требований. Так как представленное уравнение является линейным, то у учащихся может возникнуть вопрос: а зачем выяснять различные значения параметра ? Уравнение линейное – значит, всегда будет иметь одно решение.
Для ответа на этот вопрос сначала введем в рассмотрение функцию 
и построим ее график в GeoGebr’е. Сделать это достаточно просто, так как данное программное средство предоставляет возможность работы с параметрами (рис. 2.)
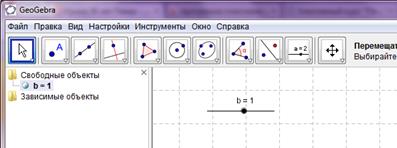
Рис. 2. Создание параметра b
С помощью инструмента «Ползунок» вставляем в документ параметр, называем его , устанавливаем диапазон от –10 до 10 (рис. 3.)
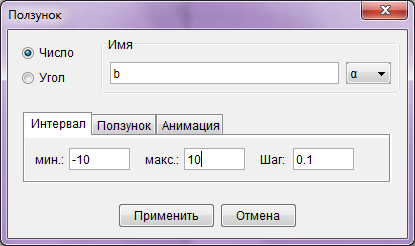
Рис. 3. Установка свойств для параметра
Затем в строке ввода записываем функцию (рис. 4.)
Рис.4. Ввод функции
На экране отразится результат (рис. 5):
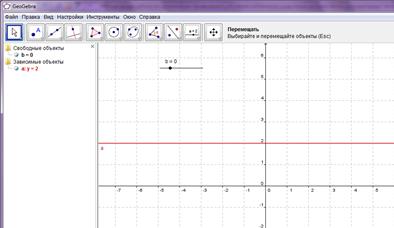
Рис. 5. Графическая иллюстрация задачи
Изменяя положение ползунка, мы получаем различные положения прямой 
. Тем самым покажем, сколько решений может иметь уравнение в зависимости от значения параметра .
При 
– нет корней (рис. 6).
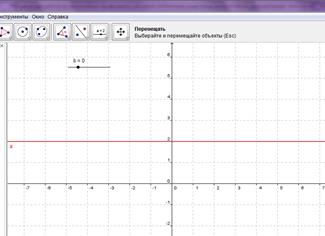
Рис. 6. Положение графика при
При 
– бесконечное множество корней (рис. 7).
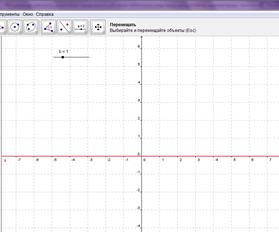
Рис. 7. положение графика при
При всех других значениях – один корень (рис. 8).
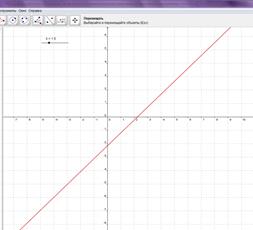
Рис. 8. Положение графика при других значениях параметра
После того как учащиеся изучили расположение графика, возможен переход к аналитическому решению.
1. Решаем систему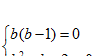
и – корни первого уравнения.
2. При второе уравнение не обращается в 0. Поэтому при исходное уравнение обращается в 0. 
, т.е. не имеет корней.
3. – корень и второго уравнения. Исходное уравнение принимает вид 0. , т.е. имеет бесконечно много корней.
4. При всех других значениях уравнение будет иметь один корень.
5. Затем самостоятельно предлагаем учащимся исследовать количество решений уравнения 
где — параметр, – неизвестная.
Теперь рассмотрим решение этого же уравнения в системе MathCad:
Решить уравнение с параметром: 
Алгоритм решения в MathCAD
1. Вводим выражение (для ввода знака равенства использовать комбинацию CTRL=)
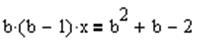
2. Выделяем переменную, относительно которой нужно решить уравнение, щелкнув по ней мышью.
3. Выбираем пункт меню Символика
4. Получаем ответ
Для других тем курса проводится аналогичная методическая работа.
Рецензенты:
Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Родионов М.А., д.п.н., профессор, профессор кафедры «Теория и методика обучения математике и информатике», ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.