Газотурбинные установки (ГТУ), которые изготавливаются на предприятиях авиационного двигателестроения, находят применение в качестве привода для электрогенераторов на электростанциях [1]. В настоящее время отечественной промышленностью налажен выпуск таких установок мощностью от 2,5 МВт до 25 МВт. Ведется разработка еще более мощных ГТУ.
Поскольку ГТУ оказываются поставленными в достаточно сложные условия работы, связанные с резкими изменениями электрической нагрузки, необходимостью обеспечить устойчивую работу электростанции как в автономном режиме работы, так и при работе на мощную внешнюю сеть, возрастают требования к системам управления ГТУ. Эти требования осложняются существенной нелинейностью такого объекта управления, каким является ГТУ [2]. Более того, при управлении ГТУ необходимо принимать во внимание не только показатели качества собственно ГТУ, но и показатели качества вырабатываемой электроэнергии. В результате рассмотрению следует подвергать нелинейную нестационарную систему, реакция которой на изменения электрической нагрузки неоднозначна. Для создания систем автоматического управления (САУ) такими объектами перспективно использовать принцип адаптивного управления. Но для введения элементов адаптации в традиционные методики управления целесообразно вначале проанализировать традиционные алгоритмы управления. В настоящей статье проводится такой анализ с тем, чтобы в дальнейшем перейти к задаче создания адаптивных САУ.
Опубликованные в статье результаты получены в рамках выполнения государственного задания Минобрнауки РФ № 13.832.2014/K «Разработка методологических основ адаптивного управления автономными и неавтономными газотурбинными электростанциями мощностью до 25 МВт».
Модель ГТУ
Для проведения исследований используются быстрорешаемые модели [3], то есть модели, требующие малого времени для проведения моделирования. Рассмотрим простейшую из полученных быстрорешаемых моделей. Эта модель относится к ГТУ мощностью 2.5 МВт на базе авиационного двигателя Д-30, ее уравнения имеют вид:
а) Уравнение ротора турбокомпрессора:
![]() . (1)
. (1)
б) Уравнение свободной турбины:
![]() . (2)
. (2)
Здесь обозначено: ![]() – частота вращения свободной турбины ГТУ (об/мин),
– частота вращения свободной турбины ГТУ (об/мин), ![]() – частота вращения турбокомпрессора ГТУ(об/мин),
– частота вращения турбокомпрессора ГТУ(об/мин), ![]() – частота вращения турбокомпрессора, взятая по нелинейной статической характеристике
– частота вращения турбокомпрессора, взятая по нелинейной статической характеристике ![]() ,
, ![]() – расход топлива (кг/час), NE – мощность свободной турбины ГТУ (кВт), NG – мощность нагрузки (кВт), J – суммарный приведенный к валу свободной турбины момент инерции, T – постоянная времени турбокомпрессора (с).
– расход топлива (кг/час), NE – мощность свободной турбины ГТУ (кВт), NG – мощность нагрузки (кВт), J – суммарный приведенный к валу свободной турбины момент инерции, T – постоянная времени турбокомпрессора (с).
Модель учитывает аккумуляцию энергии во вращающихся массах роторов двухвальной ГТУ, динамика которых описываются двумя уравнениями (1) и (2). В качестве нагрузки рассматривается синхронный генератор СГС-14-100-6 (n=1000об/мин, NG=2500кВт). Постоянная времени ротора турбокомпрессора изменяется от 3 с (на холостом ходе) до 0.5 с (номинальный режим). Величина NE – определяется по нелинейной статической характеристике ![]() .
.
По уравнениям (1), (2) получена структурная схема модели (рисунок 1). Параметры модели получены с помощью идентификации по экспериментальным данным.
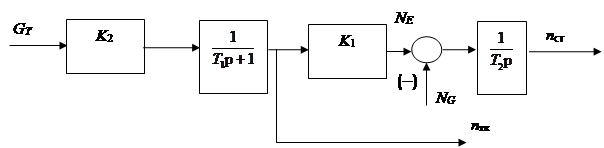
Рис.1. Линейная модель ГТУ: K2=11.1176; K1=0.26315; T1=0.5; T2=2.875
Расчет регуляторов
Структурной схеме на рисунке 1 соответствует следующая передаточная функция:
![]() (3)
(3)
Параметры регуляторов выбирают из условия получения, заданных показателей качества процессов управления (точность управления в статике, перерегулирование и время регулирования при ступенчатом входном воздействии). Наибольшее применение в инженерной практике при решении этой задачи получили два критерия оптимизации: модульный (или технический) (МО) и симметричный оптимумы (СО) [4].
Для получения МО результирующая передаточная функция (ПФ) звеньев прямой ветви должна быть равна:
![]() (4)
(4)
где Tμ – малая остающаяся некомпенсированной постоянная времени
![]() (5)
(5)
где K(p) – передаточная функция регулятора. Путем простых вычислений получаем, следующую настройку регулятора:
![]() . (6)
. (6)
Система с полученным регулятором представлена на рисунке 2:

Рис. 2. САУ, настроенная на МО: K=0,983
Для получения СО результирующая ПФ звеньев прямой ветви должна быть равна [4]:
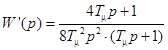 . (7)
. (7)
Получаем, следующие настройки регулятора:
![]() . (8)
. (8)
На рисунках 3 и 4 представлены графики переходных процессов САУ ГТУ при полученных настройках регуляторов.
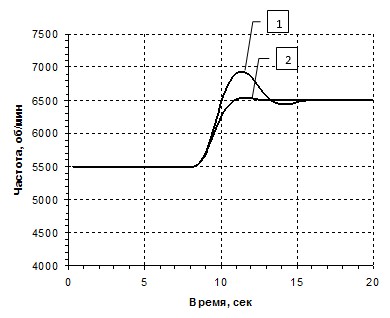
Рис. 3. Переходная характеристика с П и ПИ-регуляторами по сигналу заданию:
1– с ПИ-регулятором (СО), 2 – с П-регулятором (МО)
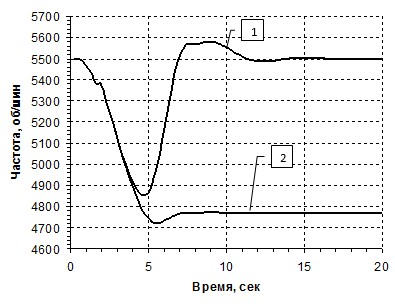
Рис. 4. Переходная характеристика с П и ПИ-регуляторами по возмущению:
1– с ПИ-регулятором (СО), 2– с П- регулятором (МО)
Оценим показатели качества для приведенных переходных процессов. По заданию (рисунок 3): перерегулирование: П-регулятор=0,65%, ПИ-регулятор=6,7%; время переходного процесса: П-регулятор=10.3 с, ПИ-регулятор=13 с. По возмущению (рисунок 4): максимальное отклонение: П-регулятор=6,9%, ПИ-регулятор=9,14%; время переходного процесса: П-регулятор=4,44 с, ПИ-регулятор=6,95с; статическая ошибка: П-регулятор=14,5%.
Введем нелинейности ![]() и
и ![]() в модель на рисунке 1, в результате получим нелинейную модель ГТУ. Результаты сравнения линейной и нелинейной моделей при броске нагрузке от холостого хода (150 кВт) до 2000 кВт приведены таблице 1.
в модель на рисунке 1, в результате получим нелинейную модель ГТУ. Результаты сравнения линейной и нелинейной моделей при броске нагрузке от холостого хода (150 кВт) до 2000 кВт приведены таблице 1.
Таблица 1
Показатели качества САУ
|
Регулятор |
Величина нагрузки, кВт |
Модель ГТУ |
Перерегули- рование, % |
Время переход. процесса, с |
Число колеба- ний |
Стат. ошибка, % |
|
П |
500 |
Линейная |
0,22 |
2,93 |
0 |
3,27 |
|
Нелинейная |
0,47 |
6,67 |
1 |
8,58 |
||
|
1000 |
Линейная |
0,45 |
3 |
0 |
6,75 |
|
|
Нелинейная |
0,94 |
7,07 |
1 |
10,91 |
||
|
2000 |
Линейная |
0,96 |
2,99 |
0 |
14,46 |
|
|
Нелинейная |
2,46 |
7,32 |
1 |
15,98 |
||
|
ПИ |
500 |
Линейная |
2,35 |
7 |
0 |
- |
|
Нелинейная |
2,8 |
8,17 |
2 |
- |
||
|
1000 |
Линейная |
4,42 |
7,1 |
0 |
- |
|
|
Нелинейная |
5,58 |
8,13 |
2 |
- |
||
|
2000 |
Линейная |
9,14 |
6,93 |
0 |
- |
|
|
Нелинейная |
11,6 |
9,46 |
2 |
- |
Как и следовало ожидать в нелинейной системе растет показатель перерегулирования, время переходного процесса, число колебаний за время переходного процесса и увеличивается статическая ошибка.
Проверим, как изменится динамика исследуемой системы при учете инерционности дозатора газа (ДГ), который представлен апериодическим звеном, включенным перед блоком K2 на рисунке 1. ПФ дозатора газа:
![]() (9)
(9)
Ранее полученные настройки не могут быть непосредственно использованы для новой структуры с ДГ. Для получения настройки на МО и СО приходится использовать систему подчиненного регулирования (каскадную систему) [4].
В каскадных системах при регулировании основной технологической величины в объекте с большим запаздыванием используются также вспомогательные величины, реагирующие на изменение основных возмущений объекта и регулирующего воздействия с меньшим запаздыванием. В таких случаях стабилизация вспомогательных величин способствует более качественному регулированию основной величины. Каскадная система состоит из нескольких контуров регулирования, каждый из которых регулирует свою технологическую (основную или вспомогательную) величину. Однако применение каскадных схем эффективно только в том случае, когда запаздывание в контуре регулирования основной величины существенно больше, чем в контуре регулирования вспомогательной величины. При автоматизации химико-технологических объектов чаще всего используют двухконтурные каскадные системы.
Структурная схема двухконтурной системы приведена на рисунке 5.
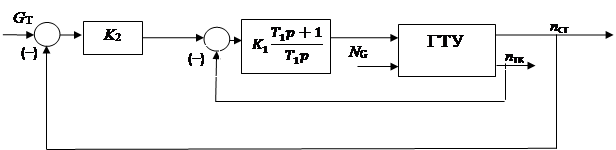
Рис. 5. САУ c подчиненным регулированием, настроенная на МО: K2=2.5; K1=0.078; T1=0.5
Регулятор внутреннего контура, где Тµ=0,2857; Тр=0,5:
![]()
![]()
![]() (10)
(10)
Тогда передаточная функция внутреннего контура может быть представлена как
![]() (11)
(11)
Передаточная функция внешнего разомкнутого контура
![]() (12)
(12)
![]() (13)
(13)
Следовательно, П-регулятор внешнего контура
![]() (14)
(14)
Аналогично получим каскадную систему, настроенную на СО. Там внешний контур, где Тµ=0.575; Тр=4Тµ=2.3, реализуется с помощью ПИ-регулятора:
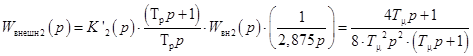 (15)
(15)
![]()
![]()
Следовательно,
![]() (16)
(16)
На рисунке 6 представлен график переходного процесса каскадной системы в сравнении с настройкой на МО без учета ДГ.
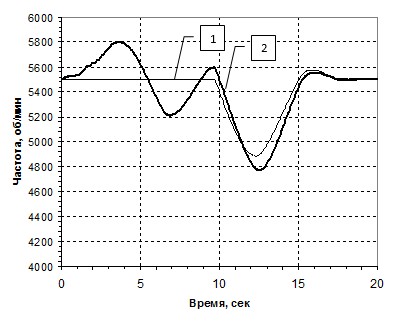
Рис. 6. Сравнение САУ, настроенных на СО: 1–линейная система с ПИ-регулятором,
2–каскадная система с ДГ
Наконец, проверим возможность настройки с ПИД-регулятором:
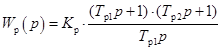 (17)
(17)
Если выбрать Тр1=0,2857; Тр2=0,5, тогда получится неустойчивая система, поэтому выберем настройку постоянной времени регулятора Тр2 = 4Тµ = 2. Таким образом, получаем следующие настройки ПИД-регулятора: KП = 8 (пропорциональное звено), KИ=0.2857 (интегрирующее звено), KД = 2 (дифференцирующее звено). График переходного процесса представлен на рисунке 7.
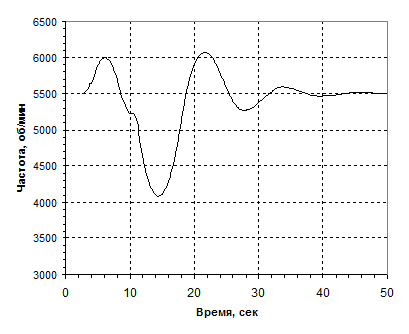
Рис. 7. Переходная характеристика САУ с ПИД-регулятором при Тр2=2
Вывод
Проведенные исследования стандартных методов управления представляют собой базу для последующего введения элементов адаптации традиционные САУ, чему будет посвящена отдельная статья. Адаптивные САУ должны своевременно реагировать на изменения параметров модели ГТУ вследствие нелинейности и нестационарности реального объекта [5].
Рецензенты:
Шулаков Н.В., д.т.н., профессор, профессор кафедры электротехники и электромеханики, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Казанцев В.П., д.т.н., профессор, профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.



