Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Рассмотрение задач длительного деформирования многих композиционных материалов и конструкций из них ведется в рамках линейной вязкоупругости анизотропных материалов.
В общем случае постановка задачи содержит несколько независимых вязкоупругих операторов (многооператорная задача вязкоупругости), отражающих различие в свойствах ползучести композитов в разных направлениях. Решение линейных многооператорных задач связано с преодолением существенных математических сложностей, поэтому во многих случаях прибегают к эффективным приближенным методам на основе принципа Вольтерра. Одним из таких методов является метод квазиконстантных операторов, в рамках которого считается, что все вязкоупругие операторы материала являются квазиконстантными [3, 7]. В ряде прикладных задач, когда внешние воздействия постоянны во времени, это означает, что приближенное решение краевой задачи вязкоупругости можно получить, заменив вязкоупругие операторы на соответствующие функции релаксации.

Рассматривается ортотропная пластинка из вязкоупругого композиционного материала с круглым отверстием радиуса и характерным размером (рис. 1). Предполагается, что . Отверстие расположено в центре пластинки, направления армирования композита совпадают с направлениями координатных осей.

Рассматриваются следующие варианты нагружения: сдвиг усилиями, параллельными главным направлениям (задача 1); касательные усилия, равномерно распределенные по кромке отверстия (задача 2); внутренне давление по кромке отверстия (задача 3) (рис. 1).

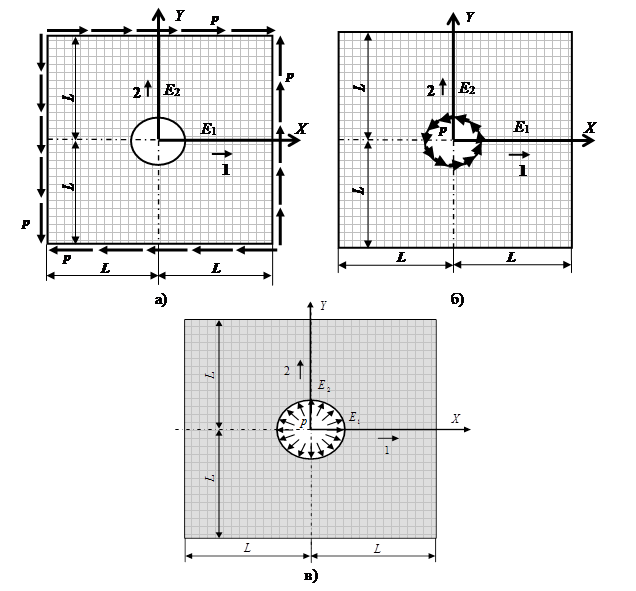
Рис. 1. Схема нагружения пластинки: а) сдвиг усилиями, параллельными главным направлениям (задача 1); б) касательные усилия, равномерно распределенные по кромке отверстия (задача 2); в) внутренне давление по кромке отверстия (задача 3)

Постановка задачи в рамках линейной теории вязкоупругости:

· уравнения равновесия: , ;

· геометрические соотношения:

· физические соотношения в условиях плоского напряженного состояния (ПНС):

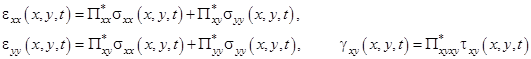(1)

где – время; , , , – интегральные операторы вида

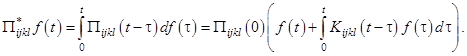(2)

Граничные условия при различных видах внешнего нагружения будут иметь вид:

· сдвиг усилиями, параллельными главным направлениям (задача 1)

, .

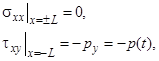
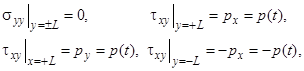
· касательные усилия, равномерно распределенные по кромке отверстия (задача 2)

,

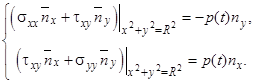
· внутренне давление по кромке отверстия (задача 3)

, , ,

.

Выше использованы следующие обозначения: – нормальные напряжения; – касательные напряжения; – линейные деформации; – сдвиговые деформации; – внешняя распределенная нагрузка.

В упругой постановке рассмотренные задачи имеют аналитические решения, приведенные в [2]. Построены конечно-элементные модели задач и выполнена проверка их точности и сходимости. Сравнение численного решения с аналитическим производилось по окружному напряжению возле кромки отверстия. Численные расчеты проведены в пакете ANSYS с использованием следующих упругих характеристик материала пластинки: Па, Па, , Па. Внешнее усилие принято постоянными , где – функция Хевисайда. Результаты приведены в табл.1.

Таблица 1

Оценка численных моделей задач

Решение поставленных краевых задач вязкоупругости произведено отдельно для материалов пластинки органопластика и стеклотекстолита, вязкоупругие свойства которых приведены в работах [5] и [1] соответственно.

В [5] приведены данные об аппроксимации кривых ползучести однонаправленного органопластика. Ядра функций ползучести приняты в виде суммы экспонент. Физические соотношения для органопластика [5] содержат четыре независимых оператора вида (2). Обращение определяющих уравнений вязкоупругой среды произведено в предположении, что все операторы являются квазиконстантными. В этом случае для любого момента времени справедливо равенство , где – тензор постоянных упругости, а – тензор постоянных податливости. Значения показатели квазиконстантности операторов приведены в табл. 2.

Таблица 2

Показатели квазиконстантности органопластика и стеклотекстолита

Характеристики ортотропной пластинки получены в виде пакета из двух ортогонально армированных однонаправленным композитом слоев: , где , – тензора постоянных упругости ортотропной пластинки и однонаправленного органопластика; – тензор постоянных упругости однонаправленного органопластика при повороте на .

Для стеклотекстолита из работы [1] определяющие уравнения содержат три независимых оператора: , и , где – дробно-экспоненциальная функция Работнова. Дальнейшие расчеты проводились в предположении, что операторы являются квазиконстантными. Значения показателей квазиконстантности определены по формуле из работы [4] и приведены в табл. 2:

,

где , , ,

, .

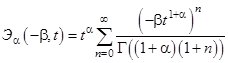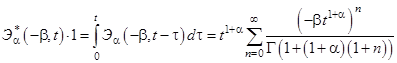Вычисление значений функций и произведено в пакете MatLab. При больших значениях аргумента использованы асимптотические разложения и связь функции с функцией Миттаг—Лаффлера [6].

Поставленные краевые задачи 1, 2, 3 для материала органопластика и стеклотекстолита решены при постоянной внешней нагрузке приближенным методом квазиконстантных операторов. Произведена оценка погрешности решения задач указанным методом. Оценка погрешности решения для материала, описываемого несколькими независимыми операторами, производится по формуле [4]:

, где – число независимых операторов.

Для каждого из слагаемых погрешности выполняется оценка , где – показатели квазиконстантности независимых операторов.

Исходя из приведенных в таблице 2 показателей квазиконстантности имеем следующие оценки погрешности: органопластик – ; стеклотекстолит – .

Задачи в упругой постановке решены численно методом конечных элементов.

На рисунке 2 в полярной системе приведены графики изменения величин для трех различных моментов времени. Здесь – окружное напряжение возле кромки отверстия, а коэффициент «0,5» имитирует отверстие радиуса 0,5, аналогично графикам, предложенным в работе [2].

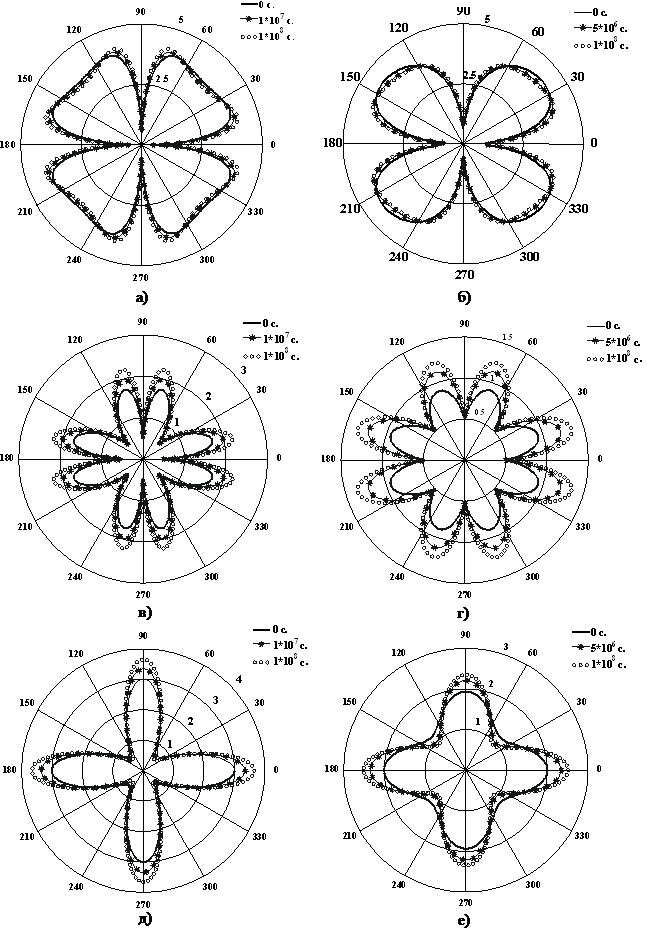
Рис. 2. Эволюция окружных напряжений у кромки отверстия.

Задача 1: а) органопластик, б) стеклотекстолит. Задача 2: в) органопластик, г) стеклотекстолит. Задача 3: д) органопластик, е) стеклотекстолит

Введем понятие коэффициента концентрации напряжений в виде , где – значение постоянной внешней нагрузки. На рисунке 3 приведены графики изменения модуля коэффициента концентрации с течением времени для угла , соответствующего наибольшему значению коэффициента в начальный момент времени.

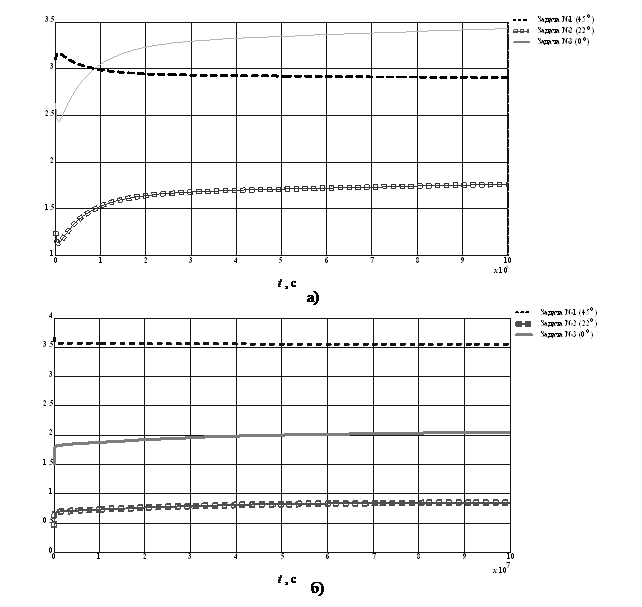
Рис. 3. Изменение коэффициента концентрации напряжений во времени возле кромки отверстия: а) органопластик; б) стеклотекстолит

Количественное изменение коэффициентов концентрации, приведенных на рис.3, представлено в табл. 3.

Таблица 3

Изменение коэффициента концентрации напряжений во времени