Важнейшей задачей обучения математике, как отмечается в федеральных государственных образовательных стандартах и программах, является обеспечение прочного и сознательного овладения учащимися математическими знаниями и умениями, нужными в повседневной жизни, достаточными как для изучения в школе, так и для продолжения образования после школы.
В исследованиях по теории и методике обучения математике (В.А. Далингер, О.Б. Епишева, Ю.М. Колягин, В.И. Крупич, Г.И. Саранцев, Л.М. Фридман и др.) показано, что задача – важнейшее средство формирования системы знаний у учащихся, развития их мышления, обучения их действиям по самостоятельному приобретению знаний [2, 3, 4].
Для того чтобы математические понятия, теоремы, законы, правила стали бы предметом учебной деятельности школьников, необходимо представить их в виде задач, которые бы направляли и стимулировали активность учащихся. Умение решать задачи является надежным критерием осознанного и творческого овладения учащимися знаниями, умениями и навыками.
Анализ школьной практики показывает, что многие учащиеся имеют формальные знания по геометрии, испытывают значительные затруднения при решении задач, в частности, планиметрических. Среди причин низкого уровня сформированности у учащихся умения решать задачи вообще и планиметрические в частности В.А. Далингер [3] отметил следующие:
- роль задач в учебном процессе понимается в узком смысле;
- количество решаемых учащимися задач наносит ущерб обучающему эффекту;
- усиленное внимание к оформлению решения, а не к процессу решения задачи;
- большинство задач, рассматриваемых на уроках, решаются по образцу;
- практически все рассматриваемые задачи даются учащимся в готовом виде, нет работы над составлением задач и их последующем решении;
- школьные курсы страдают однообразием типологии задач;
- практически нет задач, помогающих учащимся осознать способы решения (рефлексивные задачи);
- преобладание в учебниках единообразных форм предъявления задач;
- в учебниках недостает варьирования содержания задач, при сохранении метода их решения;
- имеет место большое число задач одной и той же структуры, в особенности на структуры малой сложности, что ведет к снижению интереса учащихся к решению задач и т.д.
В соответствии с положениями, сформулированными Д. Пойа, в решении задач выделяют следующие этапы: анализ условия и требований задачи, поиск плана решения, реализация намеченного плана и обоснование того, что полученный результат удовлетворяет требованиям задачи; анализ проведенного решения и полученного результата.
Психологическое обоснование этапов деятельности по решению задач, выполнение указанных элементарных шагов или умственных действий выполнено в психологических исследованиях Ж.Адамара, П.Я. Гальперина, В.В. Давыдова, Р. Декарта, Б. Паскаля, Д. Пойа, С.Л. Рубинштейна, К.А. Славской, Л.М. Фридмана, П.А. Шеварева и др. Различные сочетания элементарных шагов образуют всю деятельность по решению конкретной задачи.
Умение решать задачи – это сложное составное умение, предполагающее от учащегося умение осуществлять деятельность на каждом этапе решения задачи. Методика обучения учащихся решению задач, в том числе и геометрических, должна заключаться в обучении учащихся действиям (умениям) на каждом этапе работы над задачей. Таким образом, общая методическая схема обучения учащихся решению математических задач состоит из этапов, определяющих последовательность действий учителя:
– изучение содержания задачи (выделить данные и искомые, сделать чертеж и т.п.);
– краткая запись (записать данные и искомые задачи);
– поиск решения задачи (установить есть ли похожие задачи с известным способом решения; провести общий анализ условия задачи и т.п.);
– план решения (составить план решения на основе анализа условия задачи или сформулировать известный план решения задач данного типа);
– решение (решить задачу по составленному плану);
– запись решения, используя приемы записи;
– проверка решения (проверить ход решения, проверить результат, решить задачу другим способом, использовать специальные приемы проверки решения задач данного типа);
– исследование задачи (если возможно, то рассмотреть другие возможные способы решения, выбрать из них наиболее рациональный);
– запись ответа (полного или краткого);
– обобщение способа решения задачи, другие замечания (выполнить анализ информации, полученной в процессе решения задачи, выделить главное, обобщить, включить в систему прежнего знания о приемах работы над задачей).
Согласно федеральным государственным образовательным стандартам, основой которых является системно-деятельностный подход к обучению, все компоненты системы обучения осуществляются также на основе этого подхода. В частности, необходима деятельностная основа процесса обучения решению задач. О.Б. Епишева отмечает, что содержание учебной деятельности обучаемых должно быть преимущественно представлено в виде учебных заданий, выполняя которые на том или ином уровне, обучаемые и достигают целей образования.
Процесс обучения учащихся решению геометрических задач постепенный, который реализуется из урока в урок в течение длительного периода времени. Для реализации этого процесса в качестве основного средства можно использовать учебные задания, составленные в соответствии с основными этапами учебной деятельности по решению задач и выделенными действиями по решению задач. Ниже представлены примеры таких учебных заданий для формирования умения решать геометрические задачи на вычисление (на примере темы «Решение треугольников»).
I. Учебные задачи, направленные на формирование умения изучать содержание задачи.
1. Прочитайте задачу, выделите условие и требования задачи: Площадь треугольника АВС равна 60 см2. Найдите сторону АВ, если АС = 15 см, 
.
2. Сделайте чертеж к задаче: Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями 
.
3. По чертежу составьте условие задачи.
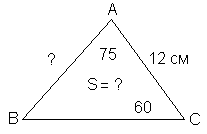
4. Обозначьте данные задачи на чертеже: У треугольника две стороны равны 5 м и 6 м, а синус угла между ними равен 0,6. Найдите третью сторону.
5. Вставьте пропущенные слова в формулировке определения или теоремы так, чтобы оно было верным:
а) единичной полуокружностью называется – полуокружность радиуса … с центром в … , расположенная в первом и втором квадрантах;
б) решением треугольника называется нахождение всех его … элементов, т.е. … сторон и … углов;
в) площадь треугольника равна половине … двух его сторон на … угла между ними;
г) квадрат стороны треугольника равен … квадратов двух других сторон … удвоенное произведение этих сторон на … угла между ними.
6. Среди предложенных формул, выберете правильную:
а) 
; б) 
; в) 
;
7. Исключите лишнюю формулу, объясните, почему:
а) ; б) 
; в) 
; г) 
.
8. Найдите ошибку в чертеже к данной задаче: основание треугольника равно 10 см, один из углов при основании равен 
, а угол, противолежащий основанию, – 
. Найдите сторону, противолежащую углу в .
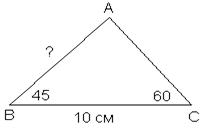
9. Определите, при каких условиях при решении треугольника по двум сторонам и углу между ними, лежащему против одной из данных сторон, задача имеет два решения.
II. Учебные задания, направленные на формирование умения осуществлять поиск решения задачи.
1. Исходя из условий задачи установите, какие понятия, свойства, теоремы, приемы необходимо использовать для ее решения: В треугольнике заданы две стороны и угол между ними. Найдите остальные два угла и сторону треугольника.
2. Ответьте на вопросы, отражающие причинно-следственные связи:
а) чтобы найти площадь треугольника надо знать…;
б) зная …, можно найти три угла треугольника (поиск решения задачи с помощью анализа или синтеза).
3. Выделите следствия из данных условий:
а) даны две стороны треугольника и угол между ними;
б) даны сторона треугольника и прилежащие к ней два угла;
в) даны три стороны треугольника.
4. Найдите площадь треугольника, если две стороны равны 10 см и 15 см соответственно, а угол между ними равен 
. Запишите формулу для нахождения площади треугольника.
5. Опишите основную идею (метод, прием) решения треугольника по стороне и двум прилегающим к ней углам.
6. Составьте алгоритм (прием) решения треугольника по трем сторонам.
7. Решите задачу: В треугольнике стороны равны 1 см, 2 см, 3 см. Найдите углы треугольника, используя известный прием решения.
8. Выберите верный чертеж к задаче: найдите биссектрисы треугольника, если одна из его сторон равна a, а прилежащие к этой стороне углы раны α и β.
а)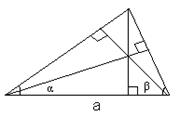 
б) 
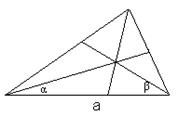в)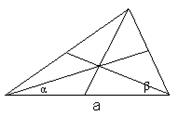 
9. Расчлените данную задачу на подзадачи: Найдите периметр равнобедренной трапеции, у которой меньшее основание равно боковой стороне, большее основание равно 10 см, а угол при основании равен 
.
10. В треугольнике АВС известны два угла α и β. Запишите теорему синусов для этого треугольника и найдите сторону в.
11. Выявите структуру данной задачи, установите зависимость, непротиворечивость условия, полноту (достаточность, недостаточность, избыточность) данных задачи: Около треугольника со сторонами 5 м, 6 м, 7 м описана окружность. Найдите радиус этой окружности.
III. Учебные задачи, направленные на формирование умения оформлять решение
1. Оформите решение задачи, используя различные приемы записи: Даны стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
2. Дана задача: Площадь треугольника АВС равна 60 см2. Найдите сторону АВ, если АС = 15 см, 
А = . Заполнить пропуски в решении:
Пусть S – площадь треугольника АВС. По теореме … S = … .
. Находим отсюда АВ = … = 16 (см).
Ответ: АВ = 16см.
3. Найдите и исправьте ошибку в оформлении задачи: с помощью теоремы синусов или косинусов решите треугольник АВС, если А = , В = 
, с = 14.
Дано: 
АВС, А = , В = , с = 14.
Найти: С, а, b.
Решение:
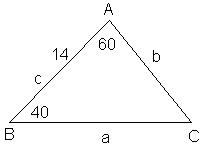
Пусть в треугольнике АВС: ВС = а, СА = b, АВ = с.
По теореме о сумме углов треугольника находим С: С = 
. По теореме синусов находим a и b: 
.
Значения синусов для данных углов определяем по таблицам. 
; 
4. Оформите решение задачи по этапам: а) изучить содержание задачи, сделать краткую запись и чертеж; б) поиск решения задачи; в) само решение; г) исследовать решение задачи и записать ответ.
Основание равнобедренного треугольника равно а, угол при противоположной вершине 2α. Найдите биссектрису, проведенную к боковой стороне.
IV. Учебные задачи, направленные на формирование умения анализировать полученное решение.
1. Запишите к данной задаче ей обратную и решите её. Стороны треугольника 5 м, 6 м, 7 м. Найдите синусы углов треугольника.
2. Найдите другой способ (прием) доказательства теоремы косинусов.
3. Определите, при каких условиях при решении треугольника по двум сторонам и углу между ними, лежащему против одной из данных сторон, задача имеет два решения.
Приведенные примеры учебных заданий дополняют задачный материал школьных учебников геометрии, дают учителю возможность осуществлять не только обучение, но и коррекцию, диагностику результатов обучения, если необходимо, то и осуществлять дифференциацию обучения учащихся.
Рецензенты:
Егорова Г.И., д.п.н., профессор, заведующий кафедрой химии и химической технологии федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тюменский государственный нефтегазовый университет» филиал в г. Тобольске, г. Тобольск;
Маллабоев У.М., д.ф.-м.н., профессор, профессор кафедры физики, математики и методик преподавания федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Тюменский государственный университет» филиал в г. Тобольске, г. Тобольск.