Для неограниченной пластины в критериальной форме система ДУЧП приобретает вид:
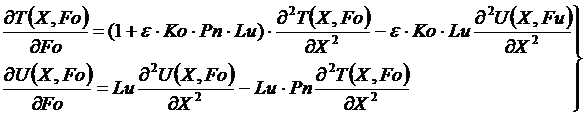 (1)
(1)
где
![]() , — безразмерная координата;
, — безразмерная координата;
Т – безразмерная температура;
U – безразмерное влагосодержание;
Fo – критерий Фурье;
Lu – критерий взаимосвязи тепло- и массопереноса;
Ko – критерий Коссовича;
Pn – критерий Поснова.
Система (1) может быть решена при различных начальных условиях. В случае низкотемпературной сушки они характеризуются следующим:
1) потенциалы переноса среды постоянны;
2) начальное распределение потенциалов переноса внутри тела постоянное (что, по мнению А.В. Лыкова [4, 5], соответствует стадии прогрева влажного тела и периода постоянной скорости сушки) либо параболическое (что соответствует падающей скорости сушки).
Следует отметить, что случай параболического распределения потенциалов носит более общий характер.
В данном случае система (1) решается при граничных условиях III рода:
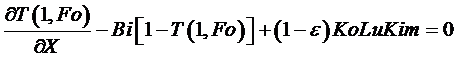 (2)
(2)
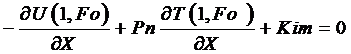 (3)
(3)
условиях симметрии:
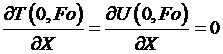 (4)
(4)
и начальных условиях:
![]() (5)
(5)
![]() (6)
(6)
где Bi – критерий Био;
Kim – массообменный критерий Кирпичева;
Bim – массообменный критерий Био;
un – влагосодержание на поверхности тела;

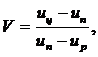 — симплексы неравномерности
начального распределения потенциалов тепло- и массопереноса;
— симплексы неравномерности
начального распределения потенциалов тепло- и массопереноса;
tп, tц, uп, uц – соответственно температура и влагосодержание поверхности и центра сортимента.
Решение системы (1) имеет вид:
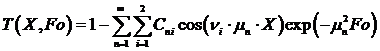 ,
(7)
,
(7)
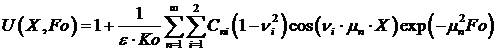 ,
(8)
,
(8)
где
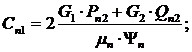
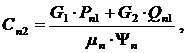 (9)
(9)
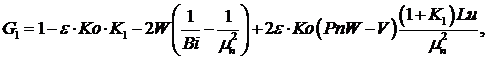 (10)
(10)
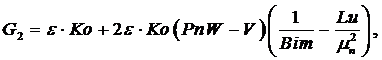 (11)
(11)
![]() (12)
(12)
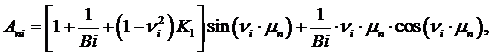 (13)
(13)
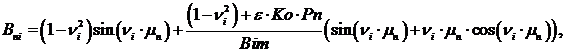 (14)
(14)
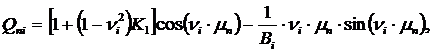 (15)
(15)
 (16)
(16)
![]()
![]() —
корни характеристического уравнения
—
корни характеристического уравнения
![]() (17)
(17)
В литературе [4, 5] приводятся некоторые решения (17), полученные графоаналитическим методом. Однако для максимального использования возможностей решения (7)–(17) необходимо хотя бы приближенное аналитическое решение характеристического уравнения (17).
Введем обозначения:
![]()
![]()
![]()
![]()
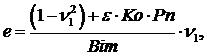
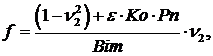
![]() ,
, ![]() ,
,
![]()
![]()
![]() (18)
(18)
После разложения тригонометрических функций в ряд Тейлора и преобразований получим:
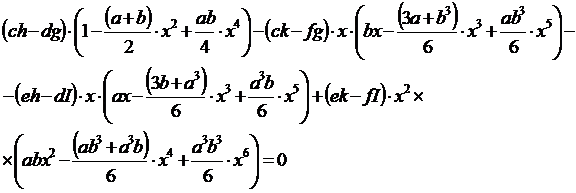 (19)
(19)
Уравнение (19) представляет собой полином 8-й степени относительно х и имеет вид:
![]() (20)
(20)
После преобразований и подстановки значений из (18) коэффициенты имеют значения:
![]()
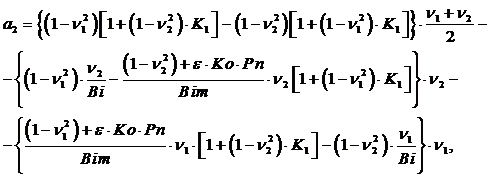
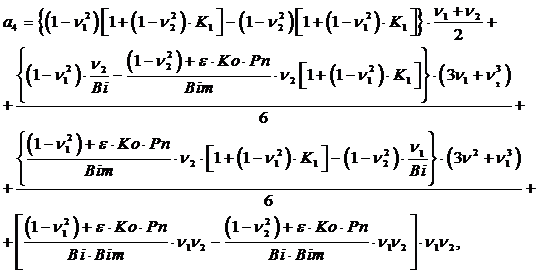
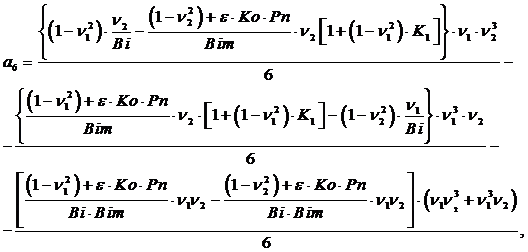
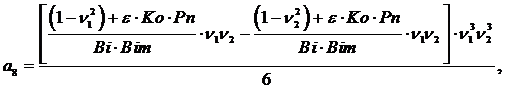
![]()
![]()
![]()
![]() (21)
(21)
В результате решения преобразованного характеристического уравнения мы можем найти 8 первых корней уравнения (17), точнее их первых приближений.
По мнению А.В. Лыкова и Ю.А. Михайлова, при замене бесконечных сумм в (7) и (8) двумя первыми членами ряда по числу корней характеристического уравнения точность вычислений может составлять 1–2%, а при количестве членов 6 и более точность может составлять 0,01–0,02%.
Предлагаемое нами решение дает возможность заменить бесконечную сумму 8 первыми членами, что позволяет говорить о точности вычислений не ниже 0,01–0,02%.
На основе предложенного метода решения системы ДУЧП тепломассообмена в вычислительной среде Mathcad-12 [2, 3] была создана программа для анализа кинетики сушки пиломатериалов.
Для нахождения корней полиномов типа (20) в Mathcad есть встроенная функция типа «V – polyroots (V)».
Пример графической интерпретации результатов решения системы ДУЧП (1) (рис. 1).
 |
а)
б) в)
Рис. 1. Кинетика сушки пиломатериалов порода – сосна, толщина – 40 мм; Wн = 60%, Wк = 12%; режим – нормативный.
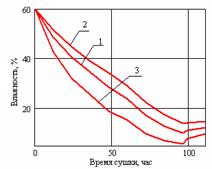
а) Изменение влажности древесины во времени:
1 – средняя влажность;
2 – внутренние слои;
3 – наружные слои.
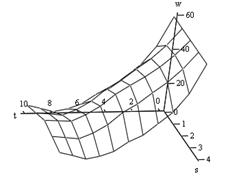
б) Распределение влажности в пространстве параметров времени и толщины доски.
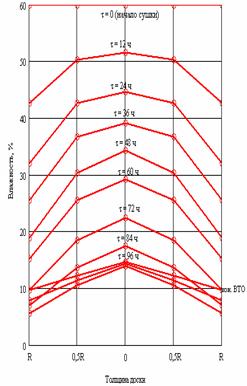
в) Распределение влажности по толщине в различные моменты времени
Рецензенты:
Санников А.А., д.т.н., профессор кафедры технической механики и оборудования целлюлозно-бумажных производств ФГБОУ ВПО «Уральский государственный лесотехнический университет», г.Екатеринбург;
Уласовец В.Г., д.т.н., профессор кафедры механической обработки древесины ФГБОУ ВПО «Уральский государственный лесотехнический университет», г.Екатеринбург.



