Овладеть навыками проведения измерений, освоить простейшие измерительные устройства студенты технических направлений ВУЗов должны, обучаясь физике уже в бакалавриате. Первые умения и навыки работы с измерительной техникой они получают в ходе выполнения физического лабораторного практикума, где опытным путем определяются необходимые величины и оцениваются точности результатов этих измерений. На первых курсах обучения в техническом ВУЗе необходимо познакомить студентов с приемами обработки полученных экспериментальных данных и методами нахождения погрешностей. Теории погрешностей в физическом лабораторном практикуме посвящено много литературы [2-4, 6, 8, 10, 11, 14, 15], однако остаются моменты, которые требуют отдельного обсуждения.
В ходе физического практикума студенту необходимо корректно измерить числовое значение физической величины и правильно сопоставить ее со значением, полученным из формулы. Кроме того, умение рассчитывать ошибки полученных величин достаточно важно, так как оно позволяет, в конечном счете, приблизится к истинному результату [8,10]. Так, результат одного и того же измерения с разной точностью может привести к противоречивым выводам. Проверка физических соотношений всегда связана с несовершенством методов измерения, приборов, а так же с различием условий проведения опытов. Поэтому умение получать измерительную информацию высокого качества и выбирать наиболее оптимальный метод измерения является существенным при обучении экспериментальным физическим методам.
Следует обратить внимание на различие в обучении обработке экспериментальных данных и расчете погрешностей студентов на уровне бакалавриата и магистратуры. Так, например, в работе [12] предлагается «исключить обработку случайных погрешностей эксперимента, основанную на нормальном распределении». Мнение автора основано на том, что студенты младших курсов (бакалавры) имеют недостаточную подготовку для проведения сложных математических вычислений случайных погрешностей прямых измерений по известным формулам. Тем более, что формулы для расчета последних не всегда пригодны. То есть в качестве результата прямого измерения физической величины обычно используется среднее арифметическое, вычисляемое по формуле
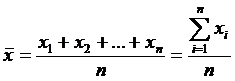 ,
,
где n – число измерений. Случайная погрешность результата прямого измерения рассчитывается как
Dхсл = ta,n×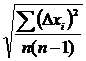 ,
,
где Dxi = xi - ![]() – случайное
отклонение результата i-го измерения
от среднего, ta,n – коэффициент
Стьюдента. Существует мнение, что при обработке небольшого числа измерений (как
правило, это 3-5 измерений в лабораторном практикуме бакалавров) нельзя пользоваться нормальной
статистикой. Нормальное распределение (распределение Гаусса) работает только
для очень большого числа случайных величин и изолированной системы, в которой
производятся измерения. Автор предлагает в лабораторных практикумах по физике
«исключить обработку случайных погрешностей эксперимента, основанную на
нормальном распределении» [12].
– случайное
отклонение результата i-го измерения
от среднего, ta,n – коэффициент
Стьюдента. Существует мнение, что при обработке небольшого числа измерений (как
правило, это 3-5 измерений в лабораторном практикуме бакалавров) нельзя пользоваться нормальной
статистикой. Нормальное распределение (распределение Гаусса) работает только
для очень большого числа случайных величин и изолированной системы, в которой
производятся измерения. Автор предлагает в лабораторных практикумах по физике
«исключить обработку случайных погрешностей эксперимента, основанную на
нормальном распределении» [12].
Следует различать уровень подготовленности студентов бакалавриата и магистратуры, а потому расчету погрешностей необходимо обучать, используя различные подходы и методики. У студентов-бакалавров, знакомящихся в ВУЗе с особенностями физической экспериментальной работы, необходимо сформировать первичные навыки обработки экспериментальных данных при небольшом числе измерений. Студентов следующей ступени, изучивших теорию вероятностей и математическую статистику, необходимо более подробно ознакомить с теорией погрешностей и показать, как эта теория работает с большими массивами данных [2]. Кроме того, необходимо научить студентов технических направлений рассчитывать погрешности и проводить проверку статистических гипотез не только в ходе стандартного лабораторного практикума, но и при выполнении научно-исследовательской и проектной работы, в которых они будут участвовать.
В начале любого физического практикума необходимо познакомить студентов бакалавриата с элементарной теорией ошибок в независимости от того, читалась ли им дисциплина «Метрология, стандартизация и сертификация» или подобный курс. Краткие сведения из теории погрешностей можно изложить в ходе вводной лекции или непосредственно в рамках лабораторного практикума по курсу общей физики. Далее закрепить начальные теоретические сведения целесообразно в ходе фронтальной лабораторной работы, целью которой будет ознакомление с методами прямых и косвенных измерений (например, линейных размеров, объёмов и масс тел; плотностей материалов) и определение погрешностей измерений [8, 10]. Необходимо объяснить обучающимся, что результат измерения никогда не может быть точным, всегда существует ошибка. Так же необходимо раскрыть источники погрешностей и методы их уменьшения. Следует сообщить студентам, что в рамках физпрактикума в бакалавриате выполняется небольшое число измерений (до 10), поэтому вычисление погрешностей «носит оценочный характер» [2]. При этом с ростом числа измерений случайная погрешность становится меньше.
Для того чтобы избежать двусмысленности в интерпретации результатов и некорректного вычисления ошибки измерения, необходимо проверить, принадлежит ли генеральная совокупность экспериментальных данных нормальному распределению. Это можно сделать следующим образом. Предварительно по каждой лабораторной работе необходимо набрать статистику в виде выборки объемом 50-100 измерений. Если мы полагаем, что распределение случайной величины описывается законом Гаусса, то проверяют эту гипотезу.
Гипотезы такого типа проверяют с помощью, так называемых критериев согласия. Чаще всего используются следующие статистические критерии: критерий Пирсона c2 (при числе измерений n > 50), критерий Мизеса-Смирнова w2 [13] и составного критерия (при числе измерений 50 > n > 15) из приложения 2 [14]. Проверку принадлежности к нормальному распределению можно проводить в соответствии с алгоритмами, описанными в [14].
Проверку гипотезы о принадлежности экспериментальных данных к распределению Гаусса проведем на примере лабораторной работы по механике «Определение ускорения свободного падения с помощью математического и оборотного маятника» [7]. Предварительно 50 раз измеряют время 5 колебаний математического маятника при длине нити 30 см. Затем можно построить гистограмму, воспользовавшись современными компьютерными программами, например Microsoft Excel или Origin Pro. Работа с этими приложениями описана в различных справочных пособиях, например в [1,16]. По внешнему виду гистограммы можно качественно оценить является ли распределение нормальным.
Для математической оценки в нашем случае (число измерений n = 50) следует воспользоваться критерием Пирсона c2 . Это позволит проверить гипотезу о нормальном распределения полученных данных. Если данная выборка будет описываться распределением Гаусса, то в последующей работе можно будет ограничиться меньшим числом измерений (n = 5 – 10), как это указано в [14].
Применение компьютерных программ в лабораторном практикуме, как отмечается в [5] имеет несколько важных аспектов. В данном случае оно позволяет уменьшить время, затрачиваемое студентом на техническую работу – обработку результатов эксперимента. Использование нами стандартных методов обработки, например Microsoft Excel или Origin Pro, не всегда дает требуемый результат, так как аппроксимация экспериментальных данных с помощью заданных функций может быть выполнена некорректно.
В связи с этим была разработана оригинальная программа, позволяющая осуществлять проверку статистических гипотез. В данной работе это проверка нормальности распределения с помощью критерия Пирсона. Программа позволяет варьировать объем выборки, при этом строится экспериментальная гистограмма, которая аппроксимируется функцией распределения Гаусса.
В результате использования
данной программы было показано, что экспериментальные данные при объеме выборки
50, подчиняются нормальному распределению. Получено значение критерия Пирсона c2 = 6,56, в то время как критическое
значение c2 крит. = 26,3 (при
доверительной вероятности 0,95). Среднее выборочное значение времени составляет
величину tср = (5,553 ![]() 0,002)
с.
0,002)
с.
Если взять меньший объем выборки n = 30, то результаты измерений также
подчиняются нормальному распределению. В этом случае среднее выборочное
значение времени составляет величину tср = (5,552 ![]() 0,002)
с. Значение критерия Пирсона c2 = 11,23 при критическом значении c2 крит. = 25 при такой же
доверительной вероятности. И наконец, для выборки n = 15, результаты измерений также описываются
распределением Гаусса. В этом случае среднее выборочное значение времени
составляет величину tср = (5,551
0,002)
с. Значение критерия Пирсона c2 = 11,23 при критическом значении c2 крит. = 25 при такой же
доверительной вероятности. И наконец, для выборки n = 15, результаты измерений также описываются
распределением Гаусса. В этом случае среднее выборочное значение времени
составляет величину tср = (5,551 ![]() 0,003)
с. Значение критерия Пирсона c2 = 13,43 при критическом значении c2 крит. = 21.
0,003)
с. Значение критерия Пирсона c2 = 13,43 при критическом значении c2 крит. = 21.
С помощью разработанной программы можно провести проверку экспериментальных данных по всем лабораторным работам курса общей физики. В зависимости от результата этой проверки для расчета случайных погрешностей можно рекомендовать студентам использование стандартных формул или, в противном случае, пользоваться упрощенным методом расчета случайной погрешности.
Кроме того, в рамках реализации двухуровневого физического практикума в бакалавриате студенты с более высоким уровнем подготовки могут рассчитывать погрешности известным способом и проводить проверку нормальности распределения экспериментальных данных, выполняя лабораторную работу на основе разработанной компьютерной программы, упомянутой выше. Менее подготовленные студенты могут выполнять измерения и проводить расчет погрешностей, пользуясь упрощенными формулами. В результате такой деятельности у обучающихся формируется представление о прямых и косвенных измерениях, осознание необходимости повторения опытов для вычисления истинного результата, о неизбежности ошибки результата любого измерения.
Рецензенты:Никитин М.А., д.ф.-м.н., профессор, профессор кафедры телекоммуникаций ФГАОУ ВПО «Балтийский федеральный университет имени Иммануила Канта», г. Калининград;
Ишанов С.А., д.ф.-м.н., профессор, директор Института прикладной математики и информационных технологий, ФГАОУ ВПО «Балтийский федеральный университет имени Иммануила Канта», г. Калининград.



