Большую группу приводных электромагнитов, с внешним по отношению к катушке якорем, совершающим ограниченное вращательное перемещение, принято [5 и др.] называть клапанными. Наиболее широкое применение [1-13] получила разновидность таких электромагнитов, питающихся от источников постоянного напряжения [9], выполненных на основе магнитной системы (рис. 1) с Г-образной скобой магнитопровода (КЭМ). Известно значительное число методик проектного расчета (определение размеров по заданным условиям функционирования) КЭМ, часть из которых указана в списке использованной литературы.
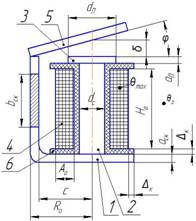Нами предпринята попытка сопоставления
известных методик проектного расчета КЭМ.
При проектировании заданы одинаковые исходные данные:
= 8 кг = 78,4 Н – механическое усилие,
которое должен преодолеть приводной электромагнит; (усилие, приведенное к оси
сердечника);
= 0,39
см = 3,9·10-3
м – рабочий воздушный зазор вдоль оси сердечника;
= 120 °С – допустимая температура нагрева
обмотки;
= 40 °С – расчетная температура окружающей
среды для электромагнитных контакторов общепромышленного применения;
– максимальное напряжение (в долях
номинального 
), которое длительно может быть приложено
к обмотке.
Результаты проектного расчета КЭМ сведены в табл. 1.
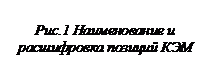В первых трех методиках, соответственно
[3, 5, 10], определение размеров 
, 
базируется на использовании
конструктивного фактора 
в зависимости от
значения которого по кривой отсчитывается магнитная индукция (
) в рабочем воздушном зазоре и
коэффициент рассеяния магнитного потока (
) в
основании сердечника (в месте сочленения сердечника с Г-образной скобой). В
рассматриваемом примере: 
кг0,5/см; 
Тл; 
.
Сечение полюсного наконечника (
) рекомендуется [5]
рассчитывать по выражению
м2.
В работе [10] – по 
м2.
В работе [3] этот момент не оговаривается;
поэтому для вычисления можно принять последнее
выражение.
Для КЭМ с круглым полюсным наконечником
диаметр () полюсного наконечника рассчитывается по
формуле 
.
Для расчета площади поперечного сечения
сердечника (
) используется 
.
Приняв в первой [5] методике 
Тл, а во второй [10] – 
Тл, согласно с последним выражением можно
получить соответственно 
мм и 
мм.
Площадь поперечного сечения (
) якоря выполняется:
в методике [5] по выражению 
м2;
в методиках [1 и 3] по выражению 
м2.
Заметим, что первоначально выбранное
значение индукции 
в методике [3] в последующем уточняется
и не является величиной «произвольно» влияющей на размеры электромагнита.
Толщина (
)
полюсного наконечника определяется [5, 10] согласно выражению
.
В [5] утверждается, что если сердечник
имеет шляпку нерационально выбирать внешний диаметр обмотки больше в
(2,5÷3) раза диаметра сердечника. Следовательно, (в среднем) можно
принять 
.
Здесь же рекомендуется целесообразная
длина (
) обмотки, составляющая 
. Выбрав 
,
имеем 
м. Ширина F-образной скобы принимается 
, а ее толщина 
.
Следовательно 
м, 
м.
Ширину якоря (
) можно принять равной 
, тогда толщина якоря 
составит 
м.
Таким образом, в соответствии с методикой [9] определены все размеры КЭМ.
Необходимая магнитодвижущая сила (
)
обмотки определяется в [10, 11]
,
где 
–
коэффициент запаса; 
– коэффициент потерь.
Приняв 
,
на среднем уровне, получим
А.
Выбирается толщина (
) каркаса катушки 
м,
коэффициенты – 
; 
(обмотка намотана на металлическую
трубу); 
–заполнения обмоточного окна; 
Вт/м2·°С – теплопередачи с наружной боковой
поверзности обмотки. Рассчитывается: внутренний диаметр обмотки: 
м;
м; 
м;
.
Полагая, что среднеобъемная температура в обмотке равна допустимой, рассчитывается удельное электрическое сопротивление обмоточной меди:
Ом·м.
Далее в методике [10, 11] рассчитывается
высота () обмотки:
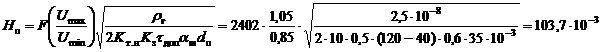м,
где
– превышение температуры поверхности (
)
охлаждения обмотки (среднеповерхностная температура обмотки принята равной
среднеобъемной).
Уточняется
коэффициент теплопередачи 
:
м2.
Вт/м2·°С.
Таблица 1
Результаты проектного расчета КМС по различным методикам
|
п/п |
Источник информации |
|
|
|
|
|
|
|
|
|
|
|
Примечание |
|
1 |
[5] |
24,3 |
|
|
41,3 |
30,4 |
3,97 |
|
|
5,0 |
|
2,5 |
|
|
2 |
[10] |
29,7 |
21 |
103,7 |
45,1 |
35,9 |
4,2 |
9,66 |
71,7 |
7,7 |
71,7 |
2,5 |
|
|
3 |
[3] |
34,0 |
10,3 |
106 |
45,1 |
29,5 |
3,97 |
8,4 |
|
8,4 |
|
|
|
|
4 |
[12,13] |
19,7 |
|
|
|
|
|
|
|
|
|
|
на основе экспериментальной усредненной безразмерной тяговой характеристики |
|
5 |
[6] |
25,7 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
[8] |
27,3 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
[7] |
25,1 |
|
|
|
|
|
|
|
|
|
|
1. Минимизация
массы активных материалов |
|
8 |
[2] |
19,8 |
|
|
|
|
|
|
|
|
|
|
1.Минимизация массы активных
материалов 2.Экспериментальная обобщенная нагрузочная характеристика |
1,7
Тл; на основе конструктивного фактора
; 
Тл (уточняется);
; 
; на основе корректирующих функций
; 
; на
основе приведенной площади поперечного сечения рабочего воздушного зазора
кг;
кг
кг; 
кг
Уточненное
значение отличается от первоначально-принятого на 5 %. В
методике [3] рекомендуется (табл. 2) задаваться отношениями 
,
. Внутренний диаметр обмотки 
уточняется
по выражению
.
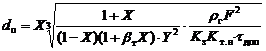Таблица 2
Основные кратности, рекомендуемые в [3]
|
Критерий оптимальности |
X |
Y |
|
Минимальные габариты |
0,62-0,69 |
1,0 |
|
Минимальная стоимость активных материалов |
0,65-0,80 |
1,8-1,9 |
При принятых X=0,65; Y=1,8 имеем
м.
м.
Расхождение составляет 
.
Принимаем 
Тл
и тогда 
м2.
м.
Расхождение 
.
Можно принять 
м.
Методика
[12,13] базируется на экспериментальных тяговых характеристиках, усредненных по
силе и представленных в безразмерной критериальной форме. При проектировании
изначально задаются кратностями (соразмерностями) в КЭМ в долях диаметра
сердечника указанными (табл. 1) над чертой: 
; 
;
; 
; 
; 
; 
; 
; 
.
На
основании формулы Максвелла при принятой первоначально индукции 
Тл
определяется 
и :
м2; 
м.
Определяется
. По безразмерной усредненной тяговой
характеристике [13] определяется 
.
А.
Рассчитывается 
А.
м.
В
соответствии с [13] определяется коэффициент 
.
Рассчитывается 
А.
Выполняются
аналогичные расчеты при 
м и 
м,
результаты которых занесены в табл. 3.
Таблица 3
К определению диаметра сердечника по методике [12,13]
|
Номер варианта |
|
|
|
|
|
1 |
26,4 |
19,4 |
3584 |
3243 |
|
2 |
27 |
19,9 |
3315 |
3365 |
|
3 |
28 |
20,6 |
3245 |
3548 |
, м
, м
, А
, А
Решив графически уравнение 
,
относительно получим 
м.
Тогда 
м.
Принимая во внимание соразмерности в КЭМ (записаны в табл. 1 над чертой) очевидным образом определяются размеры КЭМ (записаны в табл. 1 под чертой). Методика [5] предварительного (проектного) расчета электромагнитов названа «по определяющему размеру». Позже [7] она получила название метода «корректирующих функций». Суть обсуждаемой методики проиллюстрируем с использованием принятых исходных данных проектного расчета.
Выбирается основные коэффициенты
кратностей геометрических размеров КЭМ: 
; 
; 
; 
; 
.
Выбираются
основные физические параметры и коэффициенты: 
°С; 
°С; 
Вт/м2·°С; 
Вт/м2·°С; 
Ом·м; коэффициент заполнения обмоточного
окна 
; коэффициент запаса по силе 
;
.
В
КЭМ принимается допущение, что электромагнитный момент создается за счет усилия
в рабочем воздушном зазоре (
).
Для
однокатушечного КЭМ 
.
Комплекс
коэффициентов (
) запаса 
.
Комплекс физических параметров:
м3/Н.
; 
; 
; 
;
тогда комплекс коэффициентов 
.
.
; принимаем 
;
; 
.
.
.
Решая графически уравнение 
относительно
, можно определить . В
рассматриваемом примере 
. Следовательно, 
м.
При известных (принятых) кратностях геометрических размеров очевидным образом
вычислены размеры КЭМ; приведенные в табл. 1 (под чертой в строке под номером
5).
Суть методики [8], как и выше
рассмотренных [12] и [6], состоит в предварительно выбираемых кратностях
размеров КЭМ. Основное отличие заключается в том, что выражение для магнитной
проводимости [4] неравномерного поля рабочего зазора приводится к равномерному,
с площадью поперечного сечения полюса 
, которое в последующем используется в
упрощенной формуле Максвелла для расчета электромагнитной силы.
Из выражений необходимой МДС для
создания требуемой электромагнитной силы и максимально допустимой по условию
предельного нагрева (до допустимой температуры) определяется магнитная индукция
в рабочем воздушном зазоре. Далее, на основании формулы Максвелла определяется
диаметр сердечника (
м). По принятым кратностям
рассчитываются размеры КЭМ. Отметим, что по методике [8], при прочих равных
условиях, получился диаметр сердечника наиболее близкий к реальному [12] КЭМ с 
м.
В методиках[2] и [7] рассматриваются
проектные расчеты, минимизирующие массу активных материалов КЭМ (суммарной
ферромагнитной стали и обмоточной меди). Проектные расчеты в данном случае
выполнены при следующих исходных данных: 
Н;
м; 
°С; 
°С;
обмотка намотана на металлическую трубу (
);
; режим работы – длительный [7].
Выбираются [7] коэффициенты запаса для
критических условий: 
; ; 
. Выбираем кратности в КМС (в табл. 1
над чертой).
В соответствии с рекомендациями в [3]:
;
;
;
.
°С; 
°С.
Далее решается задача по методике [6] и
определяется 
м.
В строке под номером 7 таблицы 1 записаны под чертой кратности КЭМ.
В строке под номером 8 таблицы 1 записаны результаты оптимизационного расчета кратностей КЭМ (под чертой), минимизирующих массу активных материалов. Суть методики та же, что изложена в [2], изменяется лишь критерий оптимальности.
Методики [5, 10], базирующиеся на
понятии «конструктивный фактор», строго говоря справедливы при:
условно-полезной работе (
) равной 0,6 кг·см; превышении температуры нагрева
обмотки 
°С; длительном режиме работы. Без
должного обоснования выбираются: кратность высоты обмотки [5]; отношение высоты
к толщине обмотки [10,11]; магнитная индукция в основании сердечника;
коэффициенты потерь и запаса магнитодвижущей силы; коэффициенты теплопередачи:
именно эти обстоятельства приводят к значительным расхождениям при определении
диаметра сердечника (см. строки с номерами 1, 2, 3 табл. 1).
При иллюстрации методик [6, 8, 10,13] приняты
одинаковые кратности геометрических размеров (исключение составляет 
в
строке с номером 5). Наибольшее отличие рассчитанного значения диаметра
сердечника (
) от фактического значения [12] (
м)
на реальном приводном электромагните оказалось при использовании в проектной
методике экспериментальной усредненной тяговой характеристики [13]. Связано
это с тем, что обобщенная нагрузочная характеристика [1] в значительной степени
зависит от кратностей размеров КЭМ и магнитной индукции в стали.
Предпочтительны методики проектного
расчета, основанные на экспериментальных зависимостях силовых характеристик и
тепловых параметров. Они адекватно учитывают особенности топологии магнитных и
температурных полей КЭМ, позволяют минимизировать количество выбираемых
кратностей и коэффициентов, что повышает достоверность результатов синтеза.
Так, например, в методике, описанной в [2], предварительно задаются лишь
кратности не определяющих (слабо влияющих на результаты проектного расчета)
размеров КМС. Основные размеры и их кратности (
,
,
,
,
) определяются в результате минимизации
функции цели (в рассмотренном случае – массы активных материалов) и
представлены в табл. 1 (под чертой в строке с номером 7).
Выводы
1. Методики проектного расчета, базирующиеся на использовании «конструктивного фактора» могут быть рекомендованы для определения размеров клапанных электромагнитов лишь в первом приближении.
2. Использование в проектных методиках усредненной тяговой характеристики может привести к существенному искажению размеров электромагнитов, поэтому предпочтительным является использование экспериментальной обобщенной нагрузочной характеристики.
3. Предлагаемая методика оптимизационного проектного расчета клапанного электромагнита позволила определить его размеры, обеспечивающие в 1,58 раза меньшую массу активных материалов, чем известная, предложенная в [7] методика.
Исследование выполнено в рамках базовой части государственного задания Министерства образования и науки России
Афанасьев А.А., д.т.н., профессор, профессор кафедры автоматики и управления в технических системах ФГБОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова», г. Чебоксары;
Павленко А.В., д.т.н., профессор, заведующий кафедрой электромеханики и электрических аппаратов ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.