До сих пор надежность программ связывалась с методами отладки и тестирования, степенью и качеством отлаженности программ, что вполне отвечает смысловому содержанию понятия надежности. Однако с появлением проблем при разработке больших и сложных программ встает вопрос об увеличении надежности программ на уровне архитектуры, что позволит, не повышая надежности отдельных компонентов, повысить надежность программного обеспечения в целом, избежать распространения ошибки по компонентам, а также ускорит процессы поиска, анализа и устранения последствий сбоя в процессе эксплуатации [6].
Анализ архитектурной надежности программного обеспечения включает уровни, соответствующие различным компонентам и их взаимосвязи. В зависимости от того, где произошел сбой, длительность отказа и его влияние на надежность программного обеспечения различны. Сбой может происходить на различных уровнях архитектуры, в модуле, процессе, интерфейсе компонента [4]. Число архитектурных уровней в модели архитектуры зависит от проекта программного обеспечения.
В данной работе приведены аналитические выражения расчета различных показателей надежности программного обеспечения и приведен пример оценки надежности двухуровнего программного обеспечения.
Параметры надежности программного обеспечения
Параметры надежности зависят от типа архитектуры программного обеспечения, числа архитектурных уровней, компонентов и зависимостей среди компонентов [2]. Безусловные и условные вероятности сбоя программного обеспечения различны для различного числа компонентов. Безусловная вероятность сбоя зависит от количества кода в компонентах (например, может быть пропорционально количеству строк в программе или может зависеть от отношения числа измененных к общему числу строк в программе). Безусловная вероятность сбоя может также быть оценена как частота восстановлений компонента независимо от восстановления других компонентов. Условная вероятность сбоя зависит от количества кода в компонентах, зависимости компонентов и связи между компонентами. Например, условная вероятность сбоя может быть выше для компонентов, зависящих от большого числа других компонентов (при статической зависимости компонентов) или связанных с большим числом других компонентов (при динамической зависимости компонентов). Условная вероятность сбоя может также быть оценена как частота восстановления компонента, вызванного восстановлением других компонентов.
Среднее время простоя системы в архитектуре зависит от условных и безусловных вероятностей сбоев на всех уровнях архитектуры и от среднего времени доступа, анализа и восстановления сбойных компонентов [10]. Положим, что время устранения сбоя равно времени, которое требуется для доступа, анализа, восстановления. Это означает, что время восстановления меньше, чем время устранения сбоя. Среднее время простоя системы вычисляется для всех архитектурных уровней и всех компонентов на каждом уровне [7].
Для каждого архитектурного уровня программного обеспечения вероятность использования каждого компонента умножается на вероятность сбоя компонента и на сумму средних времен анализа, доступа и восстановления для этого компонента [1]. Поскольку сбойный компонент может вызывать сбои в зависящих от него компонентах, как на других уровнях архитектуры, так и на том же самом уровне, то для каждого отдельного уровня архитектуры и для всех компонентов условная вероятность появления сбоя умножается на сумму относительных времен доступа, анализа и восстановления этих компонентов. Аналогично, для одного уровня и для всех компонентов условная вероятность появления сбоя умножается на сумму относительных времен доступа, анализа и восстановления этих компонентов. Среднее время простоя системы равно:
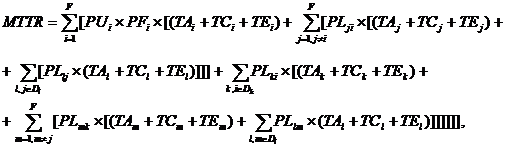 (1)
(1)
где F – общее число компонентов в архитектуре программного обеспечения; M – число уровней архитектуры программного обеспечения; Di – непересекающиеся множества компонентов на уровне i, i О {1, …, M}; PUi – вероятность использования компонента i, i О {1, …, F}; PFi – вероятность сбоя в компоненте i, i О {1, …, F}; PLij – условная вероятность сбоя в компоненте i при сбое в компоненте j, i О {1, …, F}, j О {1, …, F}; TAi – относительное время доступа к компоненту i, i О {1, …, F}; TCi – относительное время анализа сбоя в компоненте i, i О {1, …, F}; TEi – относительное время устранения сбоя в компоненте i, i О {1, …, F}.
Среднее время появления сбоя зависит от условных и безусловных вероятностей сбоев во всех компонентах на всех архитектурных уровнях и от относительного времени использования компонентов, в которых сбоя не происходит [1, 10]. Среднее время сбоя вычисляется для всех архитектурных уровней и всех компонентов на каждом архитектурном уровне. Для каждого архитектурного уровня программного обеспечения вероятность использования компонента умножается на вероятность того, что каждый компонент будет работать без сбоев в течение относительного времени его использования. Кроме этого, для каждого отдельного архитектурного уровня и для всех компонентов условная вероятность работы без сбоев умножается на относительное время использования этих компонентов. Среднее время появления сбоя равно:
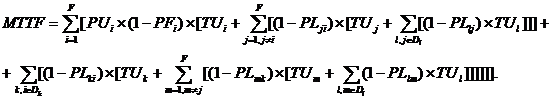 (2)
(2)
Коэффициент надежности (вероятности безотказной работы) программного обеспечения может быть оценен согласно следующей формуле:
![]() ,
(3)
,
(3)
где Ri – коэффициент (вероятности безотказной работы) надежности компонента i.
Надежность программного обеспечения можно повысить, если использовать избыточные версии компонент, например согласно мультиверсионной методологии [8, 9]. При мультиверсионном формировании состава модулей надежность каждого компонента определяется как:
![]()
где PFik – вероятность сбоя компонента из соответствующего ему множества версий Zi.
Таким образом, при увеличении надежности некоторых компонент, т.е. при уменьшении вероятности сбоя в этих компонентах, уменьшается среднее время простоя системы и увеличивается среднее время появления сбоя.
Оценка надежности программного обеспечения с двухуровневой архитектурой
Рассмотрим пример оценки показателей надежности программного обеспечения, архитектура которого имеет два уровня: уровень интерфейсов (компоненты 1–3) и уровень модулей (компоненты 4–12). Соответственно, определим два непересекающихся множества компонент Di:
D1 = {1, 2, 3},
D2 = {4, 5, 6, 7, 8, 9, 10, 11, 12}.
Архитектура рассматриваемого программного обеспечения может быть представлена посредством матрицы инцидентности графа:

Исходные данные о компонентах данного программного обеспечения представлены в таблице 1.
Таблица 1
Данные о компонентах
|
Компонент |
Ci |
PUi |
PFi |
TAi |
TCi |
TEi |
TUi |
|
1 |
300 |
0,2 |
0,05 |
1 |
3 |
2 |
400 |
|
2 |
300 |
0,1 |
0,05 |
1 |
3 |
2 |
100 |
|
3 |
300 |
0,1 |
0,05 |
1 |
3 |
2 |
150 |
|
4 |
400 |
0,05 |
0,2 |
2 |
1 |
4 |
40 |
|
5 |
200 |
0,05 |
0,05 |
2 |
1 |
4 |
40 |
|
6 |
100 |
0,6 |
0,05 |
2 |
1 |
4 |
40 |
|
7 |
200 |
0,4 |
0,05 |
2 |
1 |
4 |
40 |
|
8 |
100 |
0,7 |
0,05 |
2 |
1 |
4 |
40 |
|
9 |
200 |
0,3 |
0,05 |
2 |
1 |
4 |
40 |
|
10 |
100 |
0,08 |
0,2 |
2 |
1 |
4 |
40 |
|
11 |
200 |
0,07 |
0,2 |
2 |
1 |
4 |
40 |
|
12 |
100 |
0,15 |
0,05 |
2 |
1 |
4 |
40 |
Условная вероятность сбоя в компоненте i при сбое в компоненте j для данного программного обеспечения может быть представлена следующим образом:
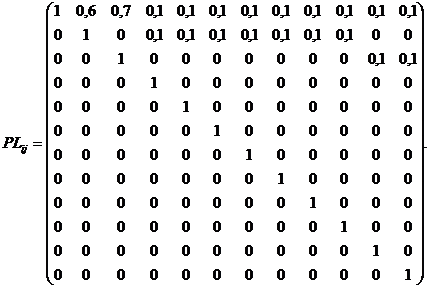
На основе представленных данных согласно выражениям (1)–(3) могут быть получены значения показателей надежности рассматриваемого программного обеспечения:
MTTR = 0,62, MTTF = 1288,94, Rs = 0,9152.
Представленные значения показателей надежности рассчитаны для архитектуры программного обеспечения без избыточности. Однако они могут быть улучшены благодаря введению дополнительных версий критичных по надежности компонентов программного обеспечения согласно мультиверсионной методологии [8, 9]. Положим, что повышенные требования по надежности предъявляются к компонентам 4, 10 и 11, поскольку именно они реализуют наиболее критичные функции. Введение избыточных версий увеличивает стоимость программного обеспечения, которая может быть рассчитана по формуле:
![]()
Различные варианты архитектур мультиверсионного программного обеспечения, а также показатели надежности и стоимость приведены в таблице 2.
Таблица 2
Варианты архитектур программного обеспечения
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
|
MTTR |
0,42 |
0,31 |
0,45 |
0,36 |
0,30 |
|
MTTF |
1536,04 |
1558,67 |
1519,02 |
1550,18 |
1558,99 |
|
Rs |
0,9238 |
0,9440 |
0,9312 |
0,9392 |
0,9524 |
|
Cs |
2700 |
2800 |
2600 |
3100 |
3200 |
В таблице 3 представлено количество версий отдельных компонентов в различных вариантах архитектур программного обеспечения с избыточностью.
Таблица 3
Количество версий компонентов в различных вариантах архитектур
|
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
Вариант 5 |
|
Компонент 1 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 2 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 3 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 4 |
2 |
1 |
1 |
2 |
2 |
|
Компонент 5 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 6 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 7 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 8 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 9 |
1 |
1 |
1 |
1 |
1 |
|
Компонент 10 |
2 |
2 |
1 |
1 |
2 |
|
Компонент 11 |
1 |
2 |
2 |
2 |
2 |
|
Компонент 12 |
1 |
1 |
1 |
1 |
1 |
Анализируя полученные результаты, можно отметить, что, вводя избыточные версии всего трех компонентов: 4, 10 и 11, при максимальном количестве версий, равном двум, повышаются значения показателей надежности всего программного обеспечения. В частности, вероятность безотказной работы увеличивается с 0,9152 до 0,9524. Если максимальное количество версий указанных компонентов увеличить до трех, то вероятность безотказной работы достигнет значения 0,9884.
Заключение
Предложенные в статье аналитические выражения позволяют выполнить оценку и анализ надежности программного обеспечения с учетом его архитектуры, числа архитектурных уровней, компонентов программного обеспечения и зависимостей между ними. В работе рассмотрены основные показатели надежности: среднее время простоя, среднее время появления сбоя, вероятность безотказной работы. Представлен пример оценки показателей надежности программного обеспечения с двухуровневой архитектурой. Показана возможность повышения надежности программного обеспечения за счет введения дополнительных версий компонентов. Предлагаемый математический аппарат целесообразно использовать при анализе и синтезе программного обеспечения, применяемого в критичных областях.
Рецензенты:
Носков М.В., д. ф.-м.н., профессор, заместитель директора по научной работе Института космических и информационных технологий Сибирского федерального университета, г. Красноярск.
Ченцов С.В., д.т.н., профессор, зав. кафедрой «Системы автоматики, автоматизированное управление и проектирование» Сибирского федерального университета, г. Красноярск.



