Анализ ФГОС ВПО по направлениям подготовки бакалавров и магистров показал, что их отличительной особенностью является значительное расширение академических свобод высших учебных заведений при разработке структуры и содержания основных образовательных программ: стандарты устанавливают лишь требования к общей структуре образовательных программ и результатам их освоения. При этом содержание предметной подготовки специалистов определяют соответствующие кафедры вуза после согласования с выпускающими кафедрами специалистов данного профиля. Возникает проблема отбора содержания предметной подготовки, для решения которой необходимо, прежде всего, определить цели обучения специалистов данному предмету.
Целью исследования является разработка принципов и методики отбора содержания математической подготовки специалистов в вузе. В качестве теоретической основы достижения поставленной цели нами выбран профессионально-деятельностный подход, базирующийся на основных положениях психолого-педагогической теории деятельности (П.Я. Гальперин, В.В. Давыдов, С.Л. Рубинштейн, С.Д. Смирнов, Н.Ф. Талызина и др.) и теории профессиональнонаправленного обучения (Г.М. Булдык, В.И. Игошин, А.Г. Мордкович, С.А. Розанова, В.В. Сериков, Л.В. Шкерина и др.). Ведущая идея данного подхода состоит в том, что при разработке целей обучения конкретному предмету, прежде всего, необходимо выделить основную систему задач, для решения которых готовится обучающийся [5, с. 6]. Главным достоинством подхода является преемственность целей разных уровней, обеспечивающая их синтез в целостную систему, и изначальная прямая связь целей с содержанием обучения. Это достигается за счет синтетического описания целей и содержания обучения на языке задач, которые должен уметь решать студент, прошедший курс обучения. Знания служат отправной точкой и результатом деятельности. Таким образом, знания не составляют самостоятельного элемента целей образования. Характеристики и свойства знания определяются характером и свойствами той деятельности, в ходе которой они сформировались и которую они могут ориентировать. Обучение обобщенным видам деятельности, адекватным задачам выделенных типов позволит выпускникам вузов успешно решать профессиональные задачи в быстро меняющихся условиях социально-экономического развития общества, т.к. обобщенные виды деятельности обладают свойством широкого переноса и применимы для решения любых конкретных задач выделенных типов. В настоящее время описанный подход использован при построении содержания обучения в разных областях и на разных образовательных ступенях (И.А. Крутова, М.Я. Микулинская, З.А. Решетова, Г.П. Стефанова, В.В. Смирнов, Н.Ф. Талызина и др.).
Ведущая идея исследования состоит в возможности выявить типы профессиональных задач специалиста, решаемых с использованием математических знаний; разработать обобщенные методы решения таких задач, что позволит однозначно определить объем и содержание опорных математических знаний, необходимых для реализации обобщенных методов. Под типовой профессиональной задачей (ТПЗ) понимаем цель, которую специалист многократно ставит перед собой в процессе выполнения профессиональной деятельности, и для достижения которой необходимы математические знания. Обобщенный метод решения ТПЗ – последовательность взаимосвязанных обобщенных действий, направленных на достижение цели ТПЗ, т.е. получение конечного продукта ТПЗ с заданными свойствами [4].
Для выделения ТПЗ необходимо провести анализ требований ФГОС ВПО к математической подготовке специалистов, анализ их квалификационных характеристик и опроситьспециалистов-практиков. В результате применения данных методов нами были выделены основные типы профессиональных задач экономиста, решаемых с применением математических знаний (ТПЗ № 1 «Обработка экономической информации», ТПЗ № 2 «Нахождение (оценка) значений параметров, характеризующих экономическую деятельность», ТПЗ № 3 «Выявление зависимости между параметрами экономической деятельности, её вида и свойств», ТПЗ № 4 «Прогнозирование экономической деятельности», ТПЗ № 5 «Планирование экономической деятельности») [4]. При этом задачи считаем принадлежащими к одному типу, если состав деятельности, адекватной этим задачам, одинаковый.
Чтобы включить ТПЗ в цели обучения математике, необходимо дополнить формулировки задач обобщенными методами их решения. Обобщенность метода решения ТПЗ понимается в том смысле, что метод применим для решения любой конкретной задачи данного типа.
Основные положения психолого-педагогической теории деятельности позволили разработать общую схему деятельности по решению типовых профессиональных задач [3]:
1. Выделить цель задачи, содержащую в формулировке конечный продукт задачи и его существенныесвойства.
2. Выделить вид деятельности, результатом или параметром которой является конечный продукт задачи.
3. Выявить предмет деятельности и его существенные свойства, которые могут быть значимыми для получения конечного продукта, отвечающего требованиям задачи.
4. Построить математическую модель исходного состояния предмета деятельности: ввести математические понятия для описания его существенных свойств и указать законы, уравнения взаимосвязей между ними.
5. Выбрать математические методы и средства деятельности на основе требований к конечному продукту деятельности или на основе свойств имеющейся математической модели предмета деятельности.
6. Составить общий план деятельности по преобразованию предмета деятельности в конечный продукт с заданными свойствами в соответствии с выбранными методами и средствами.
7. Выполнить преобразование предмета деятельности в конечный продукт с заданными свойствами в соответствии с составленным планом.
8. Выделить существенные свойства полученного в результате преобразований конечного продукта, сравнить их с планируемыми при выделении цели задачи и дать их практическую интерпретацию.
9. Скорректировать, если необходимо, математическую модель предмета деятельности, выбор методов и общий план деятельности.
Первые шесть действий соответствуют ориентировочному этапу деятельности человека по достижению поставленной цели, 7-е действие – исполнительному этапу, 8-9-е – контрольно-корректировочному этапу.
Представленная общая схема может быть положена в основу разработки обобщенных методов решения всех ТПЗ специалиста. Так, например, обобщенный метод решения ТПЗ № 4 «Прогнозирование экономической деятельности» представляет собой последовательность следующих действий [3]:
1. Сформулировать цель деятельности – оценить (с некоторой доверительной вероятностью) будущие значения параметров экономической деятельности.
2. Установить требуемый вид оценки и значение доверительной вероятности для интервального прогноза.
3. Выделить значения прогнозируемых параметров экономической деятельности.
4. Построить математическую модель экономической деятельности, являющейся объектом прогнозирования.
5. Выбрать математический метод вычисления прогнозных значений параметров экономической деятельности.
6. Разработать план вычисления прогнозных значений параметров экономической деятельности.
7. Вычислить прогнозные значения параметров экономической деятельности.
8. Проверить адекватность результатов прогнозирования.
Разработанный обобщенный метод применим для решения любых конкретных задач, относящихся к данному типу. Рассмотрим пример решения ТПЗ № 4 «Прогнозирование экономической деятельности» в соответствии с алгоритмом обобщенного метода.
Пример.По 12 предприятиям концерна изучается зависимость прибыли в тысячах рублей (у) от выработки продукции на одного человека в штуках (х). Требуется построить точечный и интервальный (с доверительной вероятностью 0.95) прогноз прибыли, если выработка составит 120 шт. на человека.
|
х |
78 |
82 |
87 |
79 |
89 |
106 |
67 |
88 |
73 |
87 |
76 |
115 |
120 |
|
у |
133 |
148 |
134 |
154 |
162 |
195 |
139 |
158 |
152 |
162 |
159 |
173 |
|
Решение
1. Цель деятельности – оценить значение прибыли предприятия, на котором выработка составляет 120 штук на одного человека.
2. Требуется получить точечный и интервальный прогноз с доверительной вероятностью 0.95 значения прибыли предприятия у (тыс. руб.), на котором выработка х (шт.) составляет 120 штук на одного человека.
3. Временной ряд значений прибыли предприятий (у) в соответствии с выработкой продукции на одного человека (х) представлен в условии задачи таблицей.
4. Методом наименьших квадратов, используя функцию ЛИНЕЙН в программе Excel, получаем оценку уравнения регрессии у(х):
|
0.920431 |
76.97649 |
|
0.279716 |
24.21156 |
|
0.519877 |
12.54959 |
|
10.82801 |
10 |
|
1705.328 |
1574.922 |
В верхней строке полученной таблицы указаны коэффициент наклона и константа, оценка уравнения (модель зависимости) имеет вид:у = 76,98 + 0,92х.
Коэффициент наклона в этом уравнении показывает предельный эффект увеличения прибыли: если выработка на одного работника увеличится на одну штуку, прибыль возрастет на 920 рублей.Коэффициент детерминации этого уравнения равен 0,52, а выборочное значение критической статистики этого коэффициента равно 10,83. С помощью функции FРАСПОБР найдем критическое значение критической статистики при уровне значимости 0,05. Это значение равно 4.964603. Мы видим, что выборочное значение больше критического, а значит качество оценивания хорошее.
5. Точечный прогноз получается непосредственной подстановкой значения выработки х = 120 в построенную модель зависимости у(х). Интервальный прогноз (доверительный интервал) получим, применяя формулы для доверительных интервалов регрессии и ошибки прогноза.
6. Составим план решения:
1) вычислить точечный прогноз значения прибыли предприятия у(120);
2) вычислить ошибку интервального прогноза;
3) вычислить коэффициент доверия tα/2;
4) вычислить границы доверительного интервала.
7.
1)
Подставив в уравнение регрессионной зависимости значение х = 120, получим точечный
прогноз значения у:![]() =
76.98 + 0.92·120 = 187.43 (тыс. руб.).
=
76.98 + 0.92·120 = 187.43 (тыс. руб.).
2) Вычислим ошибку интервального прогноза по формуле
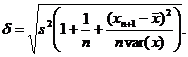
В нашем случае n = 12, ![]() 85.58333,
var(x) = 182,9924, S2 = 131,2435 (последнее значение можно
получить из таблицы функции ЛИНЕЙН). Подставив все эти значения в формулу,
получаем ошибку прогноза 14.59367.
85.58333,
var(x) = 182,9924, S2 = 131,2435 (последнее значение можно
получить из таблицы функции ЛИНЕЙН). Подставив все эти значения в формулу,
получаем ошибку прогноза 14.59367.
3) Теперь с помощью функции СТЬЮДРАСПОБР (a; n-2) вычислим правую критическую точку t-распределения для доверительной вероятности 0.95 = 1 – α (коэффициент доверия tα/2). Она равна 2.633767.
4) Границы 95% доверительного интервала
вычисляем по формуле![]() В данном случае
получаем (148.9918; 225.8645).
В данном случае
получаем (148.9918; 225.8645).
8. Полученные результаты прогнозирования адекватны данным временного ряда значений прибыли предприятий в соответствии с выработкой продукции на одного человека.
Для реализации действий обобщенного метода решения ТПЗ студенту необходимо овладеть опорными математическими знаниями. Пример выделения опорных математических знаний для реализации обобщенного метода решения ТПЗ № 4 «Прогнозирование экономической деятельности» приведен ниже в таблице 1 [2, с. 64].
Таблица 1
Опорные математические знания для реализации обобщенного метода решения ТПЗ № 4 «Прогнозирование экономической деятельности»
|
№ |
Действия обобщенного метода |
Опорные математические знания |
|
1. |
Сформулировать цель деятельности – оценить (с некоторой доверительной вероятностью) будущие значения параметров экономической деятельности |
Понятия «параметр», «значение параметра» |
|
2. |
Установить требуемый вид оценки и значение доверительной вероятности для интервального прогноза |
Понятия «точечный прогноз», «интервальный прогноз»/ «доверительная вероятность» |
|
3. |
Выделить значения прогнозируемых параметров экономической деятельности |
Понятия «независимый / зависимый параметр», «функция», «временной ряд» |
|
4. |
Построить математическую модель экономической деятельности, являющейся объектом прогнозирования |
Понятие о математических моделях описания конкретных ситуаций, структуре модели. Методы математического моделирования. Математические понятия, входящие в структуру модели |
|
5. |
Выбрать математический метод вычисления прогнозных значений параметров экономической деятельности |
Понятие о математических методах прогнозирования: методы предельного анализа функций и рядов; методы анализа временных рядов; методы регрессионного анализа; методы решения дифференциально-разностных уравнений |
|
6. |
Разработать план вычисления прогнозных значений параметров экономической деятельности |
Алгоритмы математических методов прогнозирования |
|
7. |
Вычислить прогнозные значения параметров экономической деятельности |
Правила выполнения математических действий |
|
8. |
Проверить адекватность результатов прогнозирования |
Процедуры сопоставления модельных заключений и выводов с реально наблюдаемой действительностью |
Характер выделенных опорных математических знаний позволил определить, что формирование обобщенного метода ТПЗ № 4 целесообразно осуществлять в рамках учебных математических дисциплин «Математический анализ», «Теория вероятностей», «Математическая статистика», «Эконометрика»; а также конкретизировать перечень учебных модулей данных дисциплин. В основу модульного структурирования содержания математической подготовки экономистов в вузе нами положен следующий принцип: содержание учебного модуля содержит опорные математические знания для формирования отдельных действий обобщенных методов решения ТПЗ или обобщенного метода в целом.
Если провести подобный анализ необходимых математических знаний для реализации обобщенных методов решения всех ТПЗ специалиста, то на основании полученных данных преподаватель может составить стратегический план изучения как отдельных математических дисциплин, так и математической подготовки в вузе в целом [1].
Вывод:выделение опорных математических знаний для обобщенных методов решения всех основных типов профессиональных задач специалиста позволяет однозначно и обоснованно определить структуру и содержание математической подготовки в вузе. При этом методика отбора содержания математической подготовки специалистов в вузе включает следующие виды деятельности.
1. Выделить типовые профессиональные задачи специалиста, решаемые с применением математических знаний (ТПЗ).
2. Разработать обобщенные методы решения задач выделенных типов.
3. Выделить опорные математические знания, необходимые для реализации всех действий обобщенных методов решения ТПЗ.
4. Определить в рамках каких математических дисциплин (учебных модулей) следует обучать выделенным опорным математическим знаниям.
5. Составить стратегический план математической подготовки специалистов в вузе.
Представленная методика успешно апробирована и внедрена в практику математической подготовки бакалавров по направлению «Экономика» в Астраханском государственном университете[2].
Рецензенты:Везиров Т.Г., д.п.н., профессор, профессор кафедры методики преподавания математики и информатики ФГБОУ ВПО «Дагестанский государственный педагогический университет», г. Махачкала;
Стефанова Г.П., д.п.н.,профессор, профессор кафедры теоретической физики и методики преподавания физики ФГБОУ ВПО «Астраханский государственный университет», г. Астрахань.



